Електроємність. Конденсатори
1-й семестр
ЕЛЕКТРОДИНАМІКА
1. Електричне поле
УРОК 8/8
Тема. Електроємність. Конденсатори
Мета уроку: ознайомити учнів з поняттям електричної ємності провідника.
Тип уроку: комбінований урок.
ПЛАН УРОКУ
Контроль знань | 15 хв. | Самостійна робота № 1 “Напруженість електричного поля. Провідники й діелектрики в електричному полі”. |
Демонстрації | 2 хв. | Електроємність плоского конденсатора. |
Вивчення нового | 23 хв. | 1. Що таке електроємність? 2. Конденсатор. 3. Електроємність плоского конденсатора. 4. Як обчислити електроємність батареї конденсаторів? 5. Для чого потрібні конденсатори? |
Закріплення вивченого матеріалу | 5 хв. | 1. Якісні питання. 2. Навчаємося розв’язувати задачі. |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Що таке електроємність?
Електроємність характеризує здатність провідників накопичувати електричний заряд, а отже, і електроенергію.
O Електроємність відокремленого провідника C – скалярна величина, що характеризує
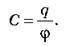
Одиницею електроємності в СІ є [C] = 1 Кл/1 В. На честь англійського фізика М. Фарадея ця одиниця названа фарадом.
1 фарад – ємність провідника, у якого зміна заряду на 1 Кл спричиняє зміну потенціалу на 1 В.
Для практичних цілей використовують малі частки фарада:
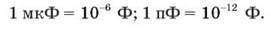
2. Конденсатор
Виявилося, що для накопичення зарядів зручно використовувати два провідники, яким передають заряди протилежних знаків, однакових за модулем.
O Конденсатор – це два провідники (обкладки), розділені шаром діелектрика, товщина якого набагато менша від розмірів провідників.
Зарядом конденсатора q називають модуль заряду однієї з його обкладок (сумарний заряд обох обкладок дорівнює нулю). Заряд конденсатора визначає напруга на цьому конденсаторі (різниця потенціалів між двома обкладками).
Для заряджання конденсатора зазвичай його обкладки з’єднують із полюсами батареї акумуляторів. Внаслідок цього на обкладках з’являються однакові за модулем, але протилежні за знаком заряди. Результат не зміниться, якщо з’єднати з полюсом батареї тільки одну обкладку, заземливши іншу.
Відношення значення q заряду цього конденсатора до різниці потенціалів (?1 – ?2) між його обкладками не залежить ні від q, ні від (?1 – ?2) і може служити характеристикою конденсатора.
O Електроємність конденсатора С – скалярна величина, що характеризує здатність конденсатора накопичувати заряд і дорівнює відношенню значення заряду q однієї з обкладок до різниці потенціалів (?1 – ?2):
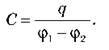
3. Електроємність плоского конденсатора
Плоский конденсатор являє собою систему із двох плоских паралельних пластин площею S кожна. Відстань між пластинами d набагато менша від їхніх лінійних розмірів.
Досліди показують, що в разі віддалення однієї пластини від другої різниця потенціалів між ними збільшується, а це свідчить про зменшення ємності конденсатора. Відповідно в разі зменшення відстані між пластинами ємність конденсатора збільшується. Тобто електроємність конденсатора змінюється обернено пропорційно відстані між пластинами:
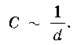
Не змінюючи відстані між пластинами, одну з них зрушуємо убік – площа пластини зменшується. Акцентуємо увагу учнів на збільшенні показань електрометра, тобто електроємність конденсатора прямо пропорційна робочій площі пластин:
C ~ S.
Дослідним шляхом можна переконатися також, що ємність конденсатора не залежить від матеріалу й товщини його пластин, але залежить від властивостей діелектрика, що перебуває між ними:
C ~ ?.
Таким чином, електроємність плоского конденсатора визначають формулою:
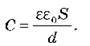
Оскільки відстань d між пластинами можна зробити дуже малою, електроємність плоского конденсатора може бути доволі значною.
4. Як обчислити електроємність батареї конденсаторів?
Розглянемо батарею, що складається із трьох конденсаторів ємностями C1, C2, C3 відповідно.
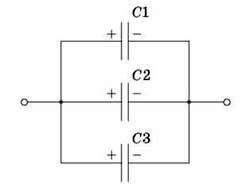
У випадку паралельного з’єднання конденсаторів, позитивно заряджені обкладки всіх конденсаторів з’єднують в один вузол, а негативно заряджені – в інший. У цьому випадку загальний заряд q батареї конденсаторів дорівнює:
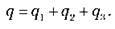
З’єднані в один вузол обкладки являють собою один провідник, тому різниця потенціалів (напруга) між обкладками всіх конденсаторів однакова:
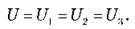
Оскільки 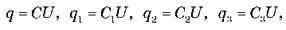 то
то
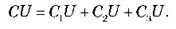
Отже, електроємність батареї конденсаторів:
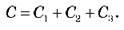
У випадку послідовного з’єднання конденсатори з’єднують між собою різнойменно зарядженими обкладками.
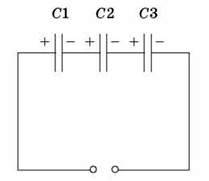
У цьому випадку потенціали різнойменно заряджених обкладок розташованих поряд конденсаторів однакові.
За послідовного з’єднання конденсаторів заряд всіх конденсаторів однаковий, тому що, наприклад, права пластина конденсатора C1 й ліва пластина конденсатора C2 утворюють замкнуту систему, повний заряд якої дорівнює нулю. Отже,
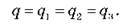
Напруга на батареї послідовно з’єднаних конденсаторів дорівнює: U = U1 + U2 + U3.
Оскільки 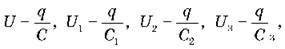 то
то
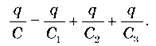
Отже, електроємність батареї конденсаторів:
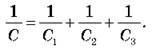
Якщо батарея конденсаторів містить n паралельно з’єднаних конденсаторів електроємністю C’ кожний, то:
C = nC’.
Якщо батарея конденсаторів містить n послідовно з’єднаних конденсаторів електроємністю C’ кожний, то:
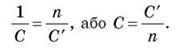
5. Для чого потрібні конденсатори?
У сучасній техніці складно знайти галузь, де б не застосовували конденсатори. Без них не може обійтися радіотехнічна й телевізійна апаратури (настроювання коливальних контурів), радіолокаційна техніка (одержання імпульсів великої потужності), телефонія й телеграфія, обчислювальна техніка, електровимірювальна техніка, лазерна техніка. І це далеко не повний перелік.
ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ
Перший рівень
1. Що таке відокремлений провідник?
2. Від чого залежить електроємність?
3. Що відбудеться з різницею потенціалів на пластинах зарядженого конденсатора, якщо зменшити відстань між ними?
4. Що відбудеться з різницею потенціалів на пластинах зарядженого конденсатора, якщо площу пластин збільшити?
Другий рівень
1. Чи правильним є твердження: під зарядом конденсатора розуміють суму зарядів його обкладок?
2. Чи зміниться різниця потенціалів пластин плоского повітряного конденсатора, якщо одну з них заземлити?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Якісні питання
1. У скільки разів зміниться ємність плоского конденсатора, якщо збільшити робочу площу пластин у 2 рази?
2. Відстань між пластинами плоского конденсатора збільшили в 4 рази. Як змінилася ємність конденсатора?
3. Для чого простір між обкладками конденсатора заповнюють діелектриком?
2). Навчаємося розв’язувати задачі
1. Чотири однакових конденсатори з’єднані в одному випадку паралельно, а в іншому – послідовно. У якому випадку ємність батареї конденсаторів більша й у скільки разів?
2. Два конденсатори ємностями 2 і 1 мкФ з’єднані послідовно й підключені до джерела напругою 120 В. Визначте напругу між обкладками першого й напругу між обкладками другого конденсаторів.
ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ
– Електроємність відокремленого провідника C – скалярна величина, що характеризує здатність провідника накопичувати заряд і дорівнює відношенню значення q електричного заряду до його потенціалу?:
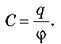
– 1 фарад – ємність провідника, у якого зміна заряду на 1 Кл спричиняє зміну потенціалу на 1 В.
– Конденсатор – це два провідники (обкладки), розділені шаром діелектрика, товщина якого набагато менше від розмірів провідників.
– Електроємність конденсатора C – скалярна величина, що характеризує здатність конденсатора накопичувати заряд і дорівнює відношенню значення заряду q однієї з обкладок до різниці потенціалів (?1 – ?2):
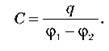
– Електроємність плоского конденсатора визначають формулою:
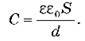
– У разі паралельного з’єднання конденсаторів загальна ємність батареї дорівнює:
C = C1 + C2.
– У разі послідовного з’єднання конденсаторів загальна ємність батареї дорівнює:
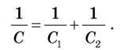
Домашнє завдання
1. Підр-1: § 7; підр-2: § 4 (п. 1, 2, 3).
2. Зб.:
Рів1 № 3.11; 3.12; 3.14; 3.15.
Рів2 № 3.25; 3.26; 3.28; 3.30.
Рів3 № 3.47, 3.48; 3.49; 3.50.