Елементи статистики
674.
Мода: 32 (зустрічається 4 рази).
Медіана: 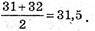
675.
1; 1; 1; 1; 2; 2; 3; 3; 3; 4; 4.
Розмах r = 4 – 1 = 3.
Мода – 1 (зустрічається 4 рази).
Медіана – 2.
676.
Частота розміру 26 дорівнює 3.
Відносна частота 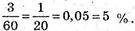
Частота розміру 29 дорівнює 9.
Розміру 26 треба виробляти в 3 рази менше, ніж розміру 29.
677.
Варіаційний ряд 1 2 3 4 5 6 6 7 8 8 8 9 13
Розмах вибірки дорівнює 12.
Мода дорівнює 8 (зустрічається 3 рази).
Медіана дорівнює 6.
678.
Частотна таблиця
Xi | 1 | 2 | 3 | 4 | 5 |
Ni | 3 | 4 | 6 | 2 | 3 |
Розмах вибірки дорівнює 4.
Мода дорівнює 3.
Медіана дорівнює 3.
679.
Частотна таблиця
Xi | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Ni | 2 | 9 | 8 | 10 | 20 | 17 | 4 | 6 | 4 |
Усього 80 абітурієнтів.
Найчастіший бал – 8, відносна частота дорівнює
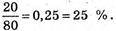
Найрідший бал – 4, відносна частота 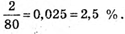
Розмах вибірки дорівнює 8.
680.
Розмах вибірки дорівнює 130 – 112 = 18.
Мода: 119.
Медіана: 120.
Відносна частота медіани
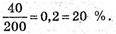
681.
А) 1, 2. З, …, 100
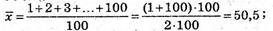
Б) -110, -109, …. 110
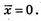
682.
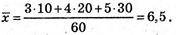
Мода: 5.
Медіана:
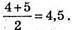
683.
21, 22, …, 49, 13, 31, 31, 32.
Варіаційний ряд
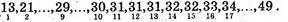
Усього 33 варіанти.
Середнє значення
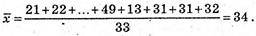
Мода:
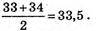
Медіана: 31 (3 рази зустрічається).
684.
Варіаційний ряд 2,0; 2,4; 2,5; 2,6; 2,7; 2,7; 2,8; 2,8; 2,9; 3,0.
Середній денний приріст маси одного бичка дорівнює
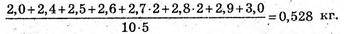
685.
Варіаційний ряд і частотна таблиця
230 | 231 | 232 | 233 | 234 | 235 | .236 | 237 | 238 | 239 | 240 |
4 | 2 | 2 | 2 | 3 | 3 | 1 | 1 | 2 | 5 | 5 |
Усього 30 випробувань.
686.
Так. Розглянемо простий приклад: 4 варіанти: 1, 2, 3, 4, середнє значення
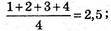 Різниці -1,5; -0,5; 0,5; 1,5, сума дорівнює 0.
Різниці -1,5; -0,5; 0,5; 1,5, сума дорівнює 0.
688.
Середній відсоток бракованих виробів дорівнює
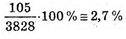
689.
Середнє арифметичне 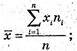
Середнє квадратичне 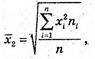
Ni – кількість повторів і варіанти;
N – загальна сума варіантів.
690.
Обчислимо середні квадратичні похибки кожного фрезерувальника:.
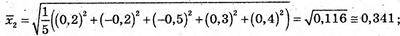
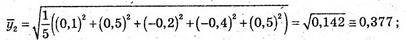
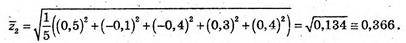
Найкраще виконав завдання перший фрезерувальник.
Related posts:
- Вступ до статистики – Початки теорії імовірностей Математика – Алгебра Початки теорії імовірностей Вступ до статистики Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки й використання статистичних даних для наукових і практичних висновків. Види статистичних спостережень: – спостереження за часовою ознакою (поточне, періодичне, одиничне); – спостереження за способом організації (звітне, експедиційне, самообчислення); – спостереження за ступенем повноти охоплення одиниць (суцільне, […]...
- Характеристики варіаційних рядів. Середні величини. Мода, медіана вибірки УРОК № 46 Тема. Характеристики варіаційних рядів. Середні величини. Мода, медіана вибірки Мета уроку: домогтися засвоєння учнями змісту понять: середнє значення, мода вибірки, медіана вибірки. Закріпити знання учнів про зміст понять, вивчених на попередньому уроці. Працювати над формуванням умінь пояснювати зміст вивчених понять, наводити приклади, що ілюструють ці поняття, а також розв’язувати задачі, що передбачають […]...
- Графічні представлення інформації про вибірки 597. Виробництво електроенергії на особу (тис. кВт × год). Країна Роки 1992 1995 2000 2005 Польща 3,5 3,8 Україна 4,5 3,23 4,2 ФРН 6,5 6,5 6,4 6,6 Франція 7,5 8,2 8,4 8,5 США 13,0 13,4 13,25 698. Підмет – роки, присудок – місця, зайняті українською командою На міжнародних математичних олімпіадах школярів. 699. 700. 701 . […]...
- МІРИ ЦЕНТРАЛЬНОЇ ТЕНДЕНЦІЇ Соціологія короткий енциклопедичний словник МІРИ ЦЕНТРАЛЬНОЇ ТЕНДЕНЦІЇ – узаг. характеристики розподілу ознаки, що відображають певну тенденцію в ряді розподілу. М. ц. т. обчислюються з метою отримати показник (одне число), який може в подальшому аналізі до певної міри “замінити” собою ряд розподілу. Обчислювати такі узагальнюючі показники ознаки є сенс лише для сукупностей, що за цією ознакою […]...
- РОЗМАХ ВАРІАЦІЙНИЙ Соціологія короткий енциклопедичний словник РОЗМАХ ВАРІАЦІЙНИЙ – Див, Міри варіації....
- Статистичні дані. Способи подання даних УРОК № 45 Тема. Статистичні дані. Способи подання даних Мета уроку: домогтися засвоєння учнями змісту понять: вибіркова сукупність, або вибірка, статистичний ряд, об’єм вибірки, частота вибірки, відносна частота вибірки, полігон частот і гістограма, а також формування уявлення учнів про предмет вивчення математичної статистики. Працювати над формуванням умінь наводити приклади подання статистичних даних у вигляді таблиць […]...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...
- ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ Основна ідея, якою пройнята вся математика, – це ідея рівності. Г. Спенсер РОЗДІЛ 3 ТРИКУТНИКИ У цьому розділі ви повторите свої знання про трикутники, здобуті в попередніх класах, і дізнаєтеся про багато інших їх властивостей. Основне в розділі – три ознаки рівності трикутників Вони часто використовуються в геометрії. Тому від того, як добре ви вивчите […]...
- Підсумкова контрольна робота з курсу математики за 5 клас Урок 126 Тема. Підсумкова контрольна робота з курсу математики за 5 клас Варіант 1 1°. Знайдіть значення виразу й округліть його до десятих: (4,1 – 0,66 : 1,2) – 0,6 + 0,125. 2°. Михайлик ішов з одного села в інше 0,7 год. полем і 0,9 год. через ліс, пройшовши 5,31 км. З якою швидкістю ішов […]...
- Відносна частота подій і випадкові величини 756. 757. Відносна частота появи жовтої грані 758. Середнє значення випадкової величини числа очок 759. 760. 761. Такий розподіл випадкової величини відповідає випаданню Очок при киданні правильного грального кубика. Такий розподіл випадкової величини відповідає випаданню Очок при киданні грального кубика октаедра. 762. Сума очок може набувати такі значення з відповідними ймовірностями Наприклад, 7 очок. Це […]...
- ШКОЛА ОПИСОВОЇ СТАТИСТИКИ Соціологія короткий енциклопедичний словник ШКОЛА ОПИСОВОЇ СТАТИСТИКИ (державознавство) – назва групи нім. дослідників – Г. Конрінг, Г. Ахенваль, А. Шлецер, М. Шмейцель та ін., які послуговувалися методами кількісного аналізу в обстеженнях соціальних процесів та явищ і заклали теорет. підгрунтя статистики як науки. Першим термін “статистика” без чіткого визначення його змісту вжив нім учений Герман Конрінг […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Середнє арифметичне, середнє значення величин Урок 113 Тема. Середнє арифметичне, середнє значення величин Мета: систематизувати знання учнів щодо понять “середнє арифметичне”, сформувати вміння учнів розв’язувати задачі високого рівня складності на застосування цих понять. Тип уроку: узагальнення і систематизація навичок, знань і вмінь. Хід уроку I. Розминка Усні вправи 1. Обчисліть: 1) 0,5 – 2,5 – 4 – 2; 2) 2 […]...
- § 11. МАСА АТОМА. АТОМНА ОДИНИЦЯ МАСИ, ВІДНОСНІ АТОМНІ МАСИ ХІМІЧНИХ ЕЛЕМЕНТІВ № 1. Атомна одиниця маси (а. о. м.) – маса 1/12 частини атома Карбону, ядро якого складається з 6 протонів і 6 нейтронів. № 2, 3. Число, яке одержують діленням маси атома конкретного хімічного елемента на атомну одиницю маси (приблизно на 1,662 • 10-27 кг) має назву відносна атомна маса хімічного елемента й позначається Аr. […]...
- Трикутник та його елементи Урок № 15 Тема. Трикутник та його елементи Мета: домогтися засвоєння учнями змісту понять: “трикутник”; “сторона, вершина, кут (внутрішній) трикутника”; “кут, протилежний стороні”; “кут, прилеглий до сторони”; “периметр трикутника”; “внутрішня та зовнішня область трикутника”. Сформувати вміння: – розпізнавати та називати елементи трикутників, зображених на рисунку; – за рисунком та символічним позначенням трикутника називати кути, протилежні […]...
- Закономірності мінливості Біологія. Експерес-підготовка до ЗНО та ДПА ТЕОРЕТИЧНІ ВІДОМОСТІ РОЗДІЛ III. ОРГАНІЗМЕНИЙ РІВЕНЬ ОРГАНІЗАЦІЇ ЖИТТЯ (продовження) Тема 7. Закономірності мінливості Усі живі організми розвиваються в тісному взаємозв’язку один з одним і з довкіллям. Різні фактори середовища (світло, температура, волога, склад грунту тощо) впливають на організми, викликаючи в них зміну зовнішніх та внутрішніх ознак. Таким чином, організм […]...
- Відносна молекулярна маса ПОСІБНИК З ХІМІЇ ДЛЯ ВСТУПНИКІВ ДО ВИЩИХ НАВЧАЛЬНИХ ЗАКЛАДІВ Частина І. ЗАГАЛЬНА ХІМІЯ Розділ 1. ОСНОВНІ ПОНЯТТЯ І ЗАКОНИ ХІМІЇ § 1.5. Відносна молекулярна маса Відносною молекулярною масою Мr речовини називається величина, що дорівнює відношенню середньої маси молекули природного ізотопічного складу речовини до маси атома карбону 12С. Відносна молекулярна маса чисельно дорівнює сумі відносних атомних […]...
- Ділення багатоцифрових чисел на двоцифрові у випадку, коли частка містить нулі УРОК 112-113 Тема. Ділення багатоцифрових чисел на двоцифрові у випадку, коли частка містить нулі Мета: опрацювати випадки ділення багатоцифрових чисел на двоцифрові, коли частка містить нулі; виробляти вміння учнів розв’язувати задачі на знаходження середнього арифметичного та задачі з буквеними даними. Обладнання: картка для усної лічби, таблиця для гри. ХІД УРОКУ I. Контроль і закріплення знань […]...
- Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...
- Ділення багатоцифрових чисел, що закінчуються нулями. Елементи куба УРОК 70 Тема. Ділення багатоцифрових чисел, що закінчуються нулями. Елементи куба Мета: ознайомити учнів з діленням багатоцифрових чисел, що закінчуються нулями, на одноцифрові; з побудовою розгортки куба; вчити визначати кількість ребер, вершин та граней куба; опрацювати ускладнену задачу на спосіб зведення до одиниці та геометричну задачу. Обладнання: таблиця та картки для усної лічби, розгортка куба. […]...
- Вправа 65-72 № 65. Маса атома – важлива характеристика атома. Відносна атомна маса – маса атома елемента в порівнянні з 1/12 масою атома Карбону. № 67. Запис Аr – відносна атомна маса (а. о. м), Аг – символ елементу Аргону. № 68. Be → Аг = 9. Al → Аr =27. Легший атом Берилію у 3 рази. […]...
- Сульфур – Елементи VIA групи ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ II. НЕОРГАНІЧНА ХІМІЯ 9. Неметалічні елементи та їхні сполуки. Неметали 9.3. Елементи VIA Групи 9.3.5. Сульфур Сульфур – 16-й елемент періодичної таблиці, заряд ядра – +16. Хімічний символ – S, відносна атомна маса – 32. Відомо чотири стабільні природні ізотопи: 32S, 33S, 34S і 36S. Електронегативність […]...
- ПІДСУМКИ РОЗДІЛУ ІІ Розділ ІІ Механічний рух ПІДСУМКИ РОЗДІЛУ ІІ – Механічним рухом називають зміну положення тіла відносно інших тіл з часом. – Швидкість руху, шлях або час можна обчислити, користуючись формулою v = . – Переміщення, швидкість і траєкторія тіла залежать від того, відносно яких тіл відліку визначається рух. – Швидкість тіла відносно нерухомої системи відліку дорівнює […]...
- Озон – Елементи VIA групи ХІМІЯ – Комплексна підготовка до зовнішнього незалежного оцінювання РОЗДІЛ II. НЕОРГАНІЧНА ХІМІЯ 9. Неметалічні елементи та їхні сполуки. Неметали 9.3. Елементи VIA Групи 9.3.4. Озон Озон O3 – це ще одна алотропна модифікація Оксигену. Відносна молекулярна маса – 48, молярна маса – 48 г/моль. Це газ зі своєрідним, різким “металічним” запахом, дуже отруйний. Озон – […]...
- Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...
- Елементи теорії пружності ФІЗИКА Частина 1 МЕХАНІКА Розділ З ОСНОВИ МЕХАНІКИ СУЦІЛЬНОГО СЕРЕДОВИЩА 3.4. Елементи теорії пружності Розглядаючи механіку твердого тіла, ми користувалися поняттям абсолютно твердого тіла. Однак у природі абсолютно твердих тіл немає, оскільки всі реальні тіла під дією сил змінюють свою форму і розміри, тобто деформуються. Деформація називається пружною, якщо після припинення дії зовнішніх сил тіло […]...
- СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР ЗАДАЧІ НА ПОВТОРЕННЯ СТЕПІНЬ НАТУРАЛЬНОГО ЧИСЛА З НАТУРАЛЬНИМ ПОКАЗНИКОМ. ПЛОЩІ ТА ОБ’ЄМИ ФІГУР 50. Обчисліть: 1)5 ∙ 26 + 22 – 4 ∙З4; 3) б2: 2 ∙ (43-55); 2) 2(2 ∙ 53- 102): 52; 4) 23: 12 ∙ 53-(32 ∙ 5-5). 51. Знайдіть значення виразу а3+ b2, якщо: 1) а = 2, b= 12; 2)а=1,b=1; […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: сформувати вміння складати системи рівнянь за умовою задачі; домогтися засвоєння схеми розв’язання задачі за допомогою системи лінійних рівнянь з двома змінними; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати вміння грамотно формулювати власні думки; – виховна: виховувати позитивне ставлення до навчання, старанність, спостережливість; Тип уроку : засвоєння нових знань, умінь, навичок. […]...
- Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...
- Неспадкова мінливість – МІНЛИВІСТЬ Біологія. Комплексний довідник – підготовка до ЗНО та ДПА ГЕНЕТИКА ТА СЕЛЕКЦІЯ МІНЛИВІСТЬ Неспадкова мінливість Неспадкова (модифікаційна) мінливість являє собою зміну фенотипу під впливом зовнішнього середовища, яка відбувається без зміни генотипу в межах норми реакції. Такі зміни фенотипу називають модифікаціями. Норма реакції – межа мінливості ознаки, зумовлена генотипом. Успадковується не ознака, а норма реакції. Вона […]...