Головна ⇒ 📌Довідник з математики ⇒ Формула коренів квадратного рівняння
Формула коренів квадратного рівняння
Математика – Алгебра
Квадратні корені
Формула коренів квадратного рівняння
Корені квадратного рівняння
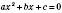
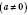
знаходять за формулою 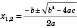 .
.
Вираз 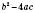 називається Дискримінантом і позначається буквою D.
називається Дискримінантом і позначається буквою D.
Кількість коренів
1. Якщо 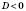 , рівняння не має коренів.
, рівняння не має коренів.
2. Якщо 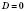 , рівняння має один корінь:
, рівняння має один корінь: 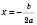 .
.
3. Якщо 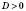 , рівняння має два корені:
, рівняння має два корені:
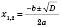 .
.
Для квадратних рівнянь із парним другим коефіцієнтом зручніше користуватися формулою, наведеною нижче.
Позначимо 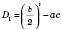 .
.
Тоді для 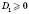 маємо
маємо 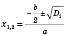 .
.
Related posts:
- Формула коренів квадратного рівняння Урок № 50 Тема. Формула коренів квадратного рівняння Мета: домогтися засвоєння учнями змісту поняття “дискримінант квадратного рівняння з парним другим коефіцієнтом”, формули дискримінанта квадратного рівняння з парним другим коефіцієнтом та формул коренів такого квадратного рівняння; сформувати первинні вміння знаходити дискримінант квадратного рівняння за новими формулами та за його значенням визначати кількість розв’язків квадратного рівняння, а […]...
- Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 54 Тема. Підсумковий урок з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: повторити, систематизувати та узагальнити знання і вміння учнів щодо виділення квадратних рівнянь серед інших рівнянь з однією змінною, класифікації квадратних рівнянь, а також застосування різних (передбачених програмою з математики) способів розв’язання квадратних рівнянь різного виду. Тип уроку: систематизація […]...
- Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Урок № 55 Тема. Тематична контрольна робота з теми “Квадратні рівняння. Формула коренів квадратного рівняння. Теорема Вієта” Мета: перевірити рівень засвоєння учнями змісту основних понять теми “Квадратні рівняння” та рівень умінь, сформованих у ході вивчення теми. Тип уроку: контроль знань та вмінь. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання Зібрати зошити із виконаною […]...
- Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Урок № 48 Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування Мета: закріпити знання учнів щодо означення квадратного рівняння, коефіцієнтів квадратного рівняння та його видів; домогтися засвоєння учнями способів розв’язання неповних квадратних рівнянь; сформувати вміння застосовувати вивчений матеріал для розв’язування неповних квадратних рівнянь. Тип уроку: засвоєння знань та вмінь. Наочність та обладнання: опорний […]...
- Розв’язування квадратного рівняння – Виділення повного квадрата Математика – Алгебра Квадратні корені Виділення повного квадрата Розв’язування квадратного рівняння Способом виділення квадратного двочлена розглянемо на прикладі. . Розв’язання Поділимо всі коефіцієнти рівняння на перший коефіцієнт: й отримаємо таким чином зведене квадратне рівняння: ; . Для того щоб отримати повний квадрат, треба додати і відняти від лівої частини рівняння : , , або , […]...
- Система двох лінійних рівнянь із двома невідомими – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Система двох лінійних рівнянь із двома невідомими – сталі. Правило Крамера: Квадратний тричлен – тричлен виду у = ах2 + bх + с, де х – змінна, а, b, с – константи і а ≠ 0. Одночлен ах2 називають старшим членом квадратного тричлена, а коефіцієнт а – старшим коефіцієнтом. Квадратний […]...
- Рівняння х2 = а. Основна тотожність квадратного кореня Урок № 36 Тема. Рівняння х2 = а. Основна тотожність квадратного кореня Мета: повторити та узагальнити знання учнів щодо способу розв’язання рівняння виду х2 = а (записати алгоритм розв’язання рівняння із використанням знань учнів про арифметичний квадратний корінь з невід’ємного числа); використовуючи означення арифметичного квадратного кореня з невід’ємного числа, сформулювати основну тотожність для квадратного кореня; […]...
- Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...
- Квадратні рівняння Тестові завдання Тестове завдання № 4 . Квадратні рівняння 1. Яке з рівнянь є квадратним? А Б В Г 7х – 3 = 0 (х – 1)2 = х2 – 4х 5х2 = 4х2 2. Знайдіть коефіцієнти a, b і с квадратного рівняння 3 – х2 – 6х = 0. А Б В Г 3; […]...
- Рівняння. Властивості рівносильності рівнянь Розв’яжіть задачі. 988. 1) 5х + 25 = 0; 5х = -25; х = -5; 2) 6у – 8 = 8; 6у = 16; у = 16/6; у= 3) 0,4x = 1,6; x = 1,6 : 0,4; x = 4; 4) 4у – 12 = 4; 4у = 16; y = 4. 989. 1) -2x […]...
- Рівняння Математика – Алгебра Натуральні числа і дії над ними Рівняння Рівність, що містить невідоме число, називається Рівнянням. Значення невідомого, при якому рівняння перетворюється у правильну числову рівність, називається Розв’язком, або Коренем рівняння. Розв’язати рівняння означає знайти всі його корені або довести, що їх немає. Кількість коренів рівняння Рівняння може: 1) не мати коренів: ; 2) […]...
- Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...
- Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники Урок № 57 Тема. Квадратний тричлен та його корені. Розкладання квадратного тричлена на лінійні множники Мета: домогтися закріплення учнями означення квадратного тричлена та його коренів, а також формули розкладання квадратного тричлена на лінійні множники; вдосконалити вміння відтворювати вивчені означення і формули та використовувати їх для розв’язування завдань на знаходження коренів квадратного тричлена та розкладання квадратного […]...
- Основні властивості арифметичного квадратного кореня – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Основні властивості арифметичного квадратного кореня Для будь-яких дійсних чисел а й b: 1) якщо а ≥ 0, , то а = ()2; 2) = |a|; 3) якщо а ≥ 0 й b ≥ 0, то = ; 4) якщо а ≥ 0 й b > 0, то ; […]...
- Рівняння та його корені. Рівносильні рівняння Урок № 4 Тема. Рівняння та його корені. Рівносильні рівняння Мета: пояснити, розширити та узагальнити відомості про властивості рівносильних рівнянь та способах їх застосування до розв’язування найпростіших рівнянь з однією змінною. Тип уроку: систематизація, поглиблення та узагальнення знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання № 1, 3 перевіряємо під час […]...
- Основні властивості рівнянь Математика – Алгебра Рівняння Два рівняння називають Рівносильними, якщо вони мають одні й ті ж корені; рівняння, які не мають коренів, також вважають рівносильними. Основні властивості рівнянь 1. Якщо виконати тотожні перетворення деякої частини рівняння, то одержимо рівняння, рівносильне даному. 2. Якщо деякий доданок перенести з однієї частини рівняння в іншу, змінивши при цьому його […]...
- Теорема Вієта Математика – Алгебра Квадратні корені Теорема Вієта Теорема 1 (Вієта). Якщо незведене квадратне рівняння має два корені, то , . Якщо зведене квадратне рівняння має два корені, то ; . Коли рівняння має один корінь, його можна вважати за два рівних: . Тоді для незведеного квадратного рівняння ; ; для зведеного , . Зверніть увагу: […]...
- Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos t = a УРОК 20 Тема. Розв’язування найпростіших тригонометричних рівнянь. Рівняння cos T = a Мета уроку: засвоєння учнями виведення і застосування формули для знаходження коренів рівняння cos t = a. Обладнання: Таблиця “Рівняння cos t = a”. І. Перевірка домашнього завдання Математичний диктант Обчисліть: 1) arcsin ; 2) arcos ; 3) arctg ; 4) arcsin; 5) arccos; […]...
- Логарифмічні рівняння УРОК 57 Тема. Логарифмічні рівняння Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виникли в учнів у процесі виконання домашніх завдань. 2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51. II. […]...
- Види неповних квадратних рівнянь і їх розв’язання Математика – Алгебра Квадратні корені Види неповних квадратних рівнянь і їх розв’язання 1. Якщо , , квадратне рівняння набуває вигляду і має один корінь . 2. Якщо , , квадратне рівняння набуває вигляду . Розв’язуючи його, маємо: ; або . Рівняння має два корені: і . 3. Якщо , , квадратне рівняння набуває вигляду . […]...
- Рівняння, що зводяться до квадратних Урок № 59 Тема. Рівняння, що зводяться до квадратних Мета: домогтися засвоєння учнями основних видів рівнянь, розв’язання яких зводиться до розв’язування квадратних рівнянь та схем їх розв’язання (дробово-раціональних рівнянь); сформувати вміння виділяти вивчені види рівнянь серед інших рівнянь, а також використовувати схеми для розв’язування названих видів рівнянь. Тип уроку: застосування знань та вмінь. Наочність та […]...
- Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...
- Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...
- Ірраціональні рівняння Математика – Алгебра Степенева функція Ірраціональні рівняння Рівняння, в яких невідоме міститься під знаком кореня, називають Ірраціональними. Розв’язуючи ірраціональні рівняння, намагаються привести їх до вигляду: , або , а потім піднести обидві частини рівняння до n-го степеня. Але якщо піднести обидві частини рівняння до парного степеня, можуть з’явитися сторонні корені. Нариклад: , ОДЗ: ; , […]...
- Рівняння. Основна властивість рівняння Урок № 96 Тема. Рівняння. Основна властивість рівняння Мета: продовжити роботу з вироблення вмінь правильно переносити доданки з однієї частини рівняння в іншу; сформувати уявлення про другу основну властивість рівнянь та розпочати роботу з вироблення вмінь використовувати множення або ділення обох частин рівняння на одне й те саме число, відмінне від 0, для розв’язування рівнянь. […]...
- Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...
- Теорема Вієта Урок № 53 Тема. Теорема Вієта Мета: закріпити знання учнів щодо змісту теореми Вієта для зведеного квадратного рівняння та для квадратного рівняння загального виду; вдосконалити вміння відтворювати вивчені твердження, використовувати їх для розв’язування завдань, передбачених програмою з математики. Тип уроку: застосування знань та вмінь. Наочність та обладнання: опорний конспект “Теорема Вієта”. Хід уроку I. Організаційний […]...
- Загальні відомості про рівняння Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 22. Загальні відомості про рівняння Упродовж багатьох століть алгебра розвивалась як наука про рівняння. Основні відомості про рівняння ви вже знаєте з попередніх класів. Нагадаємо, що вираз, записаний в рівнянні ліворуч від знака рівності, називають лівою частиною рівняння, а вираз, записаний праворуч, – правою частиною рівняння. Якщо […]...
- Лінійне рівняння з однією змінною Урок № 11 Тема. Лінійне рівняння з однією змінною Мета: перевірити рівень засвоєння знань, умінь та навичок, передбачених програмою, в ході вивчення названої теми. Тип уроку: контроль знань. Хід уроку І. Умова тематичної контрольної роботи Варіант 1 Варіант 2 № 1. Чи рівносильні рівняння? Чому? 3х + 4 = 7 та 2(х + 3) – […]...
- Квадратні корені Математика – Алгебра Квадратні корені Квадратні рівняння Квадратним рівнянням називається рівняння виду , де х – невідоме, a, b, c – деякі числа, причому . Числа a, b, c – коефіцієнти квадратного рівняння: a – перший коефіцієнт, b – другий коефіцієнт, c – вільний член. Якщо , рівняння називається Зведеним. Якщо хоча б один із […]...