Головна ⇒ 📌Довідник з математики ⇒ Формули скороченого множення
Формули скороченого множення
Математика – Алгебра
Многочлен
Формули скороченого множення
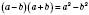 – Формула різниці квадратів.
– Формула різниці квадратів.
Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів.
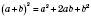 – Формула квадрата суми.
– Формула квадрата суми.
Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу.
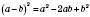 – Формула квадрата різниці.
– Формула квадрата різниці.
Квадрат різниці двох виразів дорівнює квадрату першого виразу мінус подвоєний
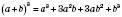 – Формула куба суми.
– Формула куба суми.Куб суми двох виразів дорівнює кубу першого виразу плюс потроєний добуток квадрата першого виразу і другого плюс потроєний добуток першого виразу і квадрата другого плюс куб другого виразу.
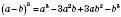 – Формула куба різниці. (Читається аналогічно попередній формулі.)
– Формула куба різниці. (Читається аналогічно попередній формулі.)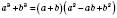 – Формула суми кубів.
– Формула суми кубів.Сума кубів двох виразів дорівнює добутку суми цих виразів і неповного квадрата їх різниці.
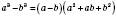 – Формула різниці кубів.
– Формула різниці кубів.Формули скороченого множення застосовуються для тотожних перетворень, зокрема для розкладання многочленів на множники.
Приклади
1) Спростити вирази:
а)
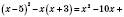
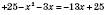 ;
;б)
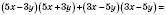
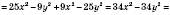
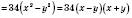 .
.2) Розв’язати рівняння:
а)
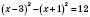 ,
,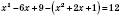 ,
,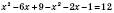 ,
,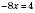 ,
, 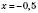 ;
;б)
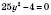 ,
,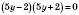 ,
,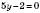 або
або 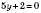 ,
,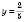 або
або 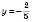 .
.3) Розкласти на множники:
а)
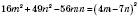 ;
;б)
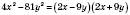 ;
;в)
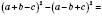
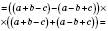
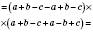
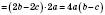 .
.4) Знайти найменше значення виразу:
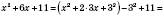
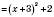 .
.Враховуючи, що
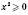 для будь-яких значень х, одержуємо, що
для будь-яких значень х, одержуємо, що 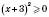 для будь-яких значень х. Найменше значення
для будь-яких значень х. Найменше значення 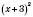 дорівнює 0, якщо
дорівнює 0, якщо 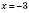 . Отже, найменше значення
. Отже, найменше значення 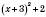 дорівнює 2 при
дорівнює 2 при 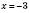 .
.Related posts:
- Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
- ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ ДО РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ Цілі: – навчальна: сформувати вміння розкладати многочлени на множники, використовуючи формули скороченого множення; – розвивальна: формувати вміння орієнтуватися у видозміненій ситуації; розвивати творчі здібності, кмітливість учнів; – виховна: виховувати інтерес до вивчення математики, наполегливість у досягненні мети; Тип уроку : засвоєння нових знань, умінь, навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ […]...
- Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Урок № 50 Тема. Використання формул скороченого множення для розкладання багаточленів на множники. Формули скороченого множення Мета: відпрацювати навички класифікації виразів та застосування формул скороченого множення для розкладання багаточленів та цілих виразів на множники та розв’язування вправ, що передбачають виконання цих Дій; повторити способи дій у разі використання формул скороченого множення для перетворення цілих виразів […]...
- Використання формул скороченого множення для розкладання багаточленів на множники Урок № 49 Тема. Використання формул скороченого множення для розкладання багаточленів на множники Мета: виробити в учнів уміння розкладати різницю квадратів та суму й різницю кубів на множники із використанням відповідних формул скороченого множення. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент Учитель спонукає учнів до само – та взаємоперевірки готовності […]...
- Квадрат двочлена Урок № 44 Тема. Квадрат двочлена Мета: відпрацювати навички застосування формул “квадрат двочлена” у стандартних ситуаціях та вдосконалити вміння застосовувати названі формули для перетворення виразів більш високою ступеня складності. Тин уроку: застосування знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ № 1 є завданням базового рівня на закріплення вмінь використовувати формули “квадрата […]...
- Формули скороченого множення Ділиться на 15. Відповідь: 5. Відповідь: 0,5. Відповідь: 1. Відповідь: 0. Відповідь: 1/2. Відповідь: 0,4. Якщо а – b = 1. Відповідь: -1. 445. х – сторона квадрата; x2 – площа квадрата; (x + 2) см – довжина прямокутника; (x – 2) см – ширина прямокутника; (x – 2)(x + 2) = (x2 – 4) […]...
- АЛГОРИТМ МНОЖЕННЯ НА ТРИЦИФРОВЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ НА ТРИЦИФРОВЕ ЧИСЛО АЛГОРИТМ МНОЖЕННЯ НА ТРИЦИФРОВЕ ЧИСЛО 932. Поясни письмове множення чисел за алгоритмом. 419 ∙ 326 419 ∙ (6 +20 + 300) 1. Підписую множники один під одним. 2. Спочатку знаходжу добуток першого множника та одиниць другого множника – 6. (Перший неповний добуток – 2 514). 3. Перший множник 419 множу […]...
- СУМА І РІЗНИЦЯ КУБІВ РОЗДІЛ 3 МНОГОЧЛЕНИ &13. СУМА І РІЗНИЦЯ КУБІВ Перелік формул скороченого множення, які ви знаєте, у цьому параграфі доповнимо ще двома формулами. Для цього спочаткy доведемо наступну теорему. Запам’ятайте! Теорема 1 (про добуток суми двох одночленів і неповного квадрата їх різниці). Добуток суми двох одночленів і неповного квадрата їх різниці дорівнює сумі кубів цих одночленів: […]...
- Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних тригонометричних функцій і формул перетворення добутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...
- КВАДРАТ ДВОЧЛЕНА РОЗДІЛ 3 МНОГОЧЛЕНИ &11. КВАДРАТ ДВОЧЛЕНА Ви вже знаєте, як додавати, віднімати і множити многочлени. Як і числа, многочлени можна підносити до степеня з натуральним показником. Для цього достатньо помножити многочлен на себе стільки разів, скільки показує число в показнику степеня. В окремих випадках піднесення до степеня дозволяє спрощувати дії з многочленами. Розглянемо їх. Запам’ятайте! […]...
- СУМА Й РІЗНИЦЯ КУБІВ Цілі: – навчальна: удосконалити вміння застосовувати формули суми й різниці кубів до розв’язування задач; – розвивальна: формувати вміння міркувати за аналогією; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати позитивне ставлення до навчання, віру у власні сили, цілеспрямованість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ […]...
- Множення різниці двох виразів на їх суму Розділ 1. ЦІЛІ ВИРАЗИ & 15. Множення різниці двох виразів на їх суму Помножимо різницю а – b на суму а + b: (а – b)(а + b) = а2 + ab – bа – b2 = а2 – b2. Отже, Одержали ще одну формулу скороченого множення. Її читають так. Розглянемо приклади застосування цієї формули. […]...
- Розкладання многочленів на множники способом групування Розділ 1. ЦІЛІ ВИРАЗИ & 13. Квадрат суми і квадрат різниці Піднесемо до квадрата двочлен а + b: (а + b)2 = (а + b)(а + b) = а2 + аb + bа + b2 = а2 + 2ab + b2. Отже, Одержану тотожність називають формулою квадрата суми. Ця тотожність дає змогу підносити до квадрата […]...
- Формули Математика – Алгебра Натуральні числа і дії над ними Формули Якщо співвідношення між якимись змінними записане у вигляді рівності, така рівність називається Формулою. Приклади Формула периметра квадрата , де P – периметр квадрата, а – сторона квадрата. Формула відстані , де s – відстань, v – швидкість, t – час. Формула площі прямокутника , де […]...
- Степінь натурального числа з натуральним показником Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 7. Степінь натурального числа з натуральним показником Уже відомо, що суму, в якій всі доданки рівні між собою, можна записати коротше – у вигляді добутку. Наприклад, У математиці є спеціальний спосіб і для запису добутку, в якому всі множники рівні між собою. […]...
- Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...
- Сума та різниця кубів Урок № 47 Тема. Сума та різниця кубів Мета: домогтися свідомого засвоєння змісту формул (a ± b)(a2 ab + b2) = a3 ± b3 та виробити базові вміння застосовувати ці формули для перетворень відповідних цілих виразів у багаточлен стандартного вигляду. Тип уроку: засвоєння знань. Хід уроку I. Організаційний момент @ Учитель перевіряє готовність учнів до […]...
- Множення. Переставна властивість множення УРОК 43 Тема. Множення. Переставна властивість множення Мета: узагальнити і систематизувати знання учнів про зміст дії множення натуральних чисел, про переставну властивість множення; властивості нуля і одиниці під час множення; формування навичок множення багатоцифрових чисел. Тип уроку: узагальнення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Прочитати число: 360; 3 600; […]...
- ЗАСТОСУВАННЯ ФОРМУЛ СКОРОЧЕНОГО МНОЖЕННЯ ДЛЯ РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ Цілі: – навчальна: удосконалити вміння розкладати многочлени на множники, використовуючи формули скороченого множення; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати старанність, уважність, скрупульозність, самостійність; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ 1. […]...
- БУКВЕНІ ВИРАЗИ. ФОРМУЛИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ У розділі дізнаєтесь: Що таке буквений вираз та як його складати; т як користуватися формулами; Про дії додавання і віднімання натуральних чисел та їх властивості; Що таке многокутник та як знаходити його периметр; Які фігури називаються рівними; Які властивості прямокутника і квадрата; Що таке трикутник, які його […]...
- Розділ 3. Многочлени 3. 1) 7×2 + х + 3; степінь 2; 2) -2х2 + 67x – 4,5; степінь 2; 3) 1,8х5 + 6х3 + 3х2 + 4х – 2,9; степінь 5; 4) 1/3×5 – 9,8х4 + 5×3 – 0,7×2 – 6; степінь 5; 5) 9,7а2b2 + 2b3а + баb + 3,75а; степінь 4; 6) 6,05b23а25 – а22b8 […]...
- Множення многочлена на многочлен Розділ 1. ЦІЛІ ВИРАЗИ & 11. Множення многочлена на многочлен Помножимо многочлен a + b на многочлен х + у. Позначимо многочлен х + у буквою m. Маємо: (а + b)(х + у) = (а + b)m = am + bm. У виразі am + bm підставимо замість m многочлен х + у і знову […]...
- МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО ПИСЬМОВЕ МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО МНОЖЕННЯ НА ДВОЦИФРОВЕ ЧИСЛО 847. Виконай множення письмово. 23 ∙ 45 230 ∙ 45 23 ∙ 450 230 ∙ 450 848. Поясни множення 254 на 39 за кроками. 1. Знаходжу перший неповний добуток. 2. Знаходжу другий неповний добуток. 3. Обчислюю їх суму. 849. 8 150 ∙ 34 2 384 ∙ […]...
- СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ РОЗДІЛ II ОДНОЧЛЕНИ &5. СТЕПІНЬ З НАТУРАЛЬНИМ ПОКАЗНИКОМ Подивіться на малюнки 3 і 4. Ви бачите квадрат зі стороною а (мал. 3) і куб з ребром а (мал. 4). Ви знаєте, як знайти площу квадрата й об’єм куба та як записати результат за допомогою відповідних виразів: а2 і а3. Узагалі, добуток n рівних множників, кожний […]...
- Розкладання многочленів на множники за допомогою формул квадрата суми і квадрата різниці Розділ 1. ЦІЛІ ВИРАЗИ & 14. Розкладання многочленів на множники За допомогою формул квадрата суми і квадрата різниці Формули квадрата суми і квадрата різниці можна використовувати також для розкладання на множники виразів вигляду а2 + 2аb + b2 і а2 – 2ab +b2. Для цього перепишемо ці формули, помінявши місцями їх ліву і праву частини. […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- РІЗНИЦЯ КВАДРАТІВ РОЗДІЛ 3 МНОГОЧЛЕНИ &12. РІЗНИЦЯ КВАДРАТІВ Ви вже знаєте, що таке формули скороченого множення, і вмієте користуватися формулами квадрата суми двох одночленів і квадрата різниці двох одночленів. Ще одну формулу дістанемо, довівши наступну теорему. Запам’ятайте! Теорема (про добуток суми і різниці двох одночленів). Добуток суми і різниці двох одночленів дорівнює різниці їх квадратів: (а + […]...
- Самостійна робота. Дія множення. Переставний, сполучний і розподільний закони множення (№№ 531-540) Тема. Самостійна робота. Дія множення. Переставний, сполучний і розподільний закони множення (№№ 531-540). Мета. Узагальнити уявлення учнів про дію множення; повторити взаємозв’язки між величинами “відстань”, “швидкість”, “час”; перевірити обчислювальні навички та вміння розв’язувати задачі, рівняння, нерівності. Обладнання. Таблиця “Множення на одноцифрове число”; “Картки для поточного та тематичного контролю знань”; набірне полотно з предметними малюнками. Зміст […]...
- МНОЖЕННЯ ВИДУ 208 ∙ 135 ПИСЬМОВЕ МНОЖЕННЯ НА ТРИЦИФРОВЕ ЧИСЛО МНОЖЕННЯ ВИДУ 208 ∙ 135 941. Добуток двох чисел дорівнює 0, їх частка теж 0. Якими можуть бути ці два числа? Досліди. 942. Поясни покрокове письмове множення чисел. 1. Підписую множники один під одним. 2. Обчислюю перший неповний добуток (добуток нуля і будь-якого числа є нулем). 3. Обчислюю другий неповний […]...
- Повторення. Арифметичні дії додавання, віднімання, множення і ділення Повторення. Арифметичні дії додавання, віднімання, множення і ділення 1 Розкажи, що тобі відомо про арифметичні дії додавання, віднімання, множення і ділення. Згадай закони і правила арифметичних дій. 2 Обчисли зручним способом, за бажанням використовуючи правила та закони арифметичних дій. (56 738 + 42 607) – 24 738 (125 ∙ 56) ∙ 8 83 129 – […]...