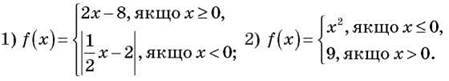ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ ФУНКЦІЇ
Цілі:
– навчальна: сформувати поняття функції, аргументу та значення функції; домогтися засвоєння способів задання функції; сформувати вміння розв’язувати задачі, які передбачають застосування цих понять;
– розвивальна: формувати культуру усного та писемного мовлення; розвивати увагу, логічне мислення, пам’ять;
– виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, працьовитість;
Тип уроку : засвоєння нових знань, умінь, навичок.
Обладнання та наочність:
Хід уроку
І.
______________________________________________________
______________________________________________________
______________________________________________________
ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ
1. Перевірка завдання, заданого за підручником
______________________________________________________
______________________________________________________
2. Самостійна робота з подальшою перевіркою та обговоренням
Варіант 1 | Варіант 2 |
1) Опівночі температура повітря була +6 °С. До 8 години температура підвищувалася рівномірно на 0,5 °С за кожну годину | 1) Опівночі температура повітря була -4 °С. До 7 години температура знижувалася рівномірно на 2 °С |
А) Запишіть формулу, яка виражає зміну температури повітря (у) залежно від зміни часу (x); Б) побудуйте графік залежності температури від часу; В) знайдіть за допомогою графіка температуру повітря: о 2 годині, о 6 годині; о 7 годині |
ІІІ. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
План вивчення теми
1. Означення функції. Аргумент та значення функції.
2. Способи задання функції:
1) аналітичний; 2) табличний; 3) описовий; 4) графічний.
3. Приклади задання функцій різними способами:
______________________________________________________
______________________________________________________
IV. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І ВМІНЬ
1. Робота за підручником
______________________________________________________
______________________________________________________
2. Додаткові завдання
Задайте формулою функцію, задану описово:
1) значення функції дорівнюють значенням аргументу;
2) значення функції удвічі менші від значень аргументу;
3) значення функції на 1 більші, ніж подвоєні значення аргументу.
V. ПІДСУМКИ УРОКУ
1.
______________________________________________________
______________________________________________________
2. Виконання усних вправ
1) Авіапасажири сидять у кріслах авіалайнера. Нехай X – множина пасажирів, Y – множина крісел. Чи є відповідність між множинами X і Y функцією, якщо:
А) кожен пасажир сидить на своєму місці й усі місця зайняті;
Б) кожен пасажир сидить на своєму місці й одне місце вільне;
В) на одному місці сидять два пасажири (наприклад, мати з дитиною);
Г) один пасажир сидить одразу на двох місцях?
2) Функцію задано: формулою f(х) = 2х +1;
Таблицею
Х | -2 | -1 | 0 | 1 | 2 |
Y | -3 | -1 | 1 | 3 | 5 |
Описово: значення функції дорівнює подвоєному аргументу, збільшеному на 1;
Графічно:
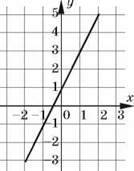
А) У кожному з випадків знайдіть f(-2); f(0); f(0,5); f(2); f(3). Чи у всіх випадках можна виконати це завдання?
Б) У яких випадках задано одну й ту саму функцію?
VI. ДОМАШНЄ ЗАВДАННЯ
1. Завдання за підручником:
______________________________________________________
______________________________________________________
2. Додаткове завдання. Знайдіть значення функції, що відповідають значенням аргументу -4; 0; 6, якщо: