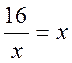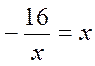Функція y=k/x, її властивості і графік
Урок № 30
Тема. Функція 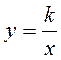 , її властивості і графік
, її властивості і графік
Мета: закріпити знання учнів щодо означення й основних властивостей функції 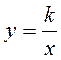 та її графіка; сформувати сталі вміння застосувати набуті знання в розв’язуванні завдань базового, середнього та достатнього рівнів, зміст яких відповідає програмовим вимогам; поглибити знання учнів про сферу застосування властивостей функції (графіка функції) уявленням про графічний спосіб розв’язання рівнянь з однією змінною.
та її графіка; сформувати сталі вміння застосувати набуті знання в розв’язуванні завдань базового, середнього та достатнього рівнів, зміст яких відповідає програмовим вимогам; поглибити знання учнів про сферу застосування властивостей функції (графіка функції) уявленням про графічний спосіб розв’язання рівнянь з однією змінною.
Тин уроку: застосування
Наочність та обладнання: опорний конспект “Функції”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Для урізноманітнення роботи з навчальним матеріалом на етані перевірки домашнього завдання можна провести роботу у формі “Знайди помилку”.
Для “сильних” учнів пропонуємо індивідуальні завдання на картках.
III. Формулювання мети і завдань уроку
На етапі формулювання мети уроку доречними будуть слова вчителя про те, що властивості функцій, які вивчаються в середній школі (і не тільки), цікаві самі по собі (бо, відображуючи реальні
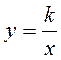 для графічного розв’язання рівнянь.
для графічного розв’язання рівнянь.IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчальною матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: означення та основні властивості функції 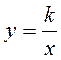 властивості її графіка; означення та основні властивості лінійної функції, властивості її графіка; оперативні вміння роботи з рівнянням, що задає функцію (за поданим значенням аргументу знайти відповідне значення функції, і навпаки – знайти, при якому значенні аргументу функція набуває нового значення; перевірити обчисленням, чи належить точка із заданими координатами графіку функції, рівняння якої відоме).
властивості її графіка; означення та основні властивості лінійної функції, властивості її графіка; оперативні вміння роботи з рівнянням, що задає функцію (за поданим значенням аргументу знайти відповідне значення функції, і навпаки – знайти, при якому значенні аргументу функція набуває нового значення; перевірити обчисленням, чи належить точка із заданими координатами графіку функції, рівняння якої відоме).
Контрольні запитання
1. Дайте означення оберненої пропорційності.
2. Для функції 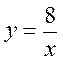 заповніть таблицю:
заповніть таблицю:
Х | 2 | -8 |
У | – 2 | -4 |
3. Порівняйте властивості графіків функцій 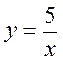 і
і 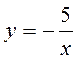 .
.
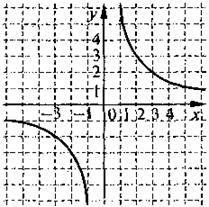
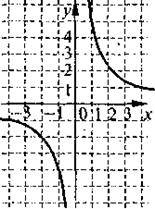
4. Який із наведених графіків найбільш точно відповідає рівнянню 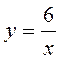 ?
?
А) | Б) | В) |
|
|
|
V. Засвоєння знань
План вивчення нового матеріалу
1. Алгоритм графічного розв’язання рівняння з однією змінною.
2. Приклад застосування алгоритму графічного розв’язання рівняння з однією змінною.
@ Алгоритм розв’язання рівняння з однією змінною графічним способом не с матеріалом, обов’язковим для вивчення у 8 класі. Проте з метою підготовки учнів до ЗНО (завдання якого передбачають уміння розв’язувати рівняння з параметрами, а багато рівнянь із параметром зручно розв’язувати саме графічним способом), а також для підвищення рівня математичної культури на уроці можна запропонувати учням опрацювати названий спосіб розв’язання рівнянь. При цьому рівень складності завдань учитель визначає сам, виходячи з реального рівня знань та вмінь учнів.
V. Відпрацювання вмінь
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв’язати завдання такого змісту:
1. Графічне розв’язування рівнянь з однією змінною.
1) Знайдіть координати точок перетину графіків функцій: а) 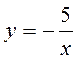 І у = х – 4,5; б)
І у = х – 4,5; б) 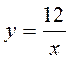 і у = -2х + 1.
і у = -2х + 1.
2) Розв’яжіть графічно рівняння: а) 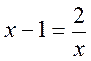 ; б)
; б)  .
.
2. Задання оберненої пропорційності, якщо задана точка її графіка.
1) Обернена пропорційність задана формулою 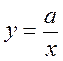 . Знайдіть а, якщо у = 2 при х = 0,5.
. Знайдіть а, якщо у = 2 при х = 0,5.
2) Запишіть формулу оберненої пропорційності, якщо її графіку належить: а) точка А(-3; 12); б) точка В(8; 4).
3. Задання за допомогою оберненої пропорційності залежності між певними фізичними величинами.
1) Учень має певну суму грошей, на яку він може купити 12 зошитів за ціною 0,4 гри. Скільки зошитів за ціноюb гри може купити учень на цю ж суму?
2) Сила струму у провіднику становить 2 А, а його опір – 40 Ом. Провідником якого опору потрібно замінити провідник, щоб сила струму дорівнювала у ампер при тій самій напрузі?
4. Додатково (для сильних учнів): побудувати графік функції, яка перетворюється на обернену пропорційність шляхом тотожних перетворень рівняння цієї функції на її області визначення.
1) Знайдіть область визначення функції і побудуйте її графік:
А) 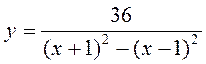 ; б)
; б) 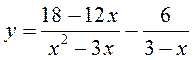 ; в)
; в) 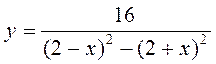 ; г)
; г) 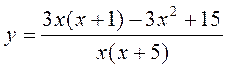 .
.
2) Побудуйте графік функції: а) 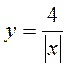 ; б)
; б) 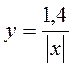 ; в)
; в) 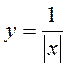 ; г)
; г) 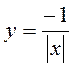 ; д)
; д) 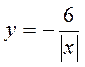 ; є)
; є) 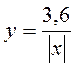 .
.
5. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) При яких значеннях k і b гіпербола 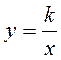 та пряма у = kх + b проходять через точку: a) P(2; 1); б) Q(-2; 3); в) R(-1; 1)?
та пряма у = kх + b проходять через точку: a) P(2; 1); б) Q(-2; 3); в) R(-1; 1)?
2) Чи можуть графіки функції 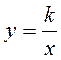 і у = ах + b перетинатися:
і у = ах + b перетинатися:
А) тільки в одній точці; б) тільки у двох точках; в) у трьох точках?
3) Чи можуть графіки функцій 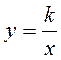 і у = ах + b перетинатися удвох точках, які лежать: а) в одній чверті; б) у першій і другій чвертях; в) у першій і третій чвертях?
і у = ах + b перетинатися удвох точках, які лежать: а) в одній чверті; б) у першій і другій чвертях; в) у першій і третій чвертях?
4) Знайдіть пропущений вираз:
Сn+3 | Сn-5 | С8 |
5а9b16 | А8b20 | ? |
6. На повторення: вправи на застосування властивостей степеня з цілим показником, вправи, що передбачають розв’язування раціональних, дробових рівнянь.
1) Розв’яжіть рівняння: a) (4x – 1)(4x + 1) – 3 = 15х2; б) (3х – 2)2 – 9×2 = 7; в) 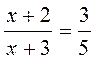 ; г)
; г) 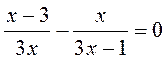 .
.
2) Обчисліть: а) 81 • 3-3; б) 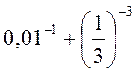 ; в) (-2,5)-1 : 1,5-2; г) 3-4 • 33 + 2-4 • 25; д) (4-4)-4 : 230; е)
; в) (-2,5)-1 : 1,5-2; г) 3-4 • 33 + 2-4 • 25; д) (4-4)-4 : 230; е) 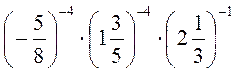 .
.
3) Перетворіть вираз так, щоб він не містив степенів із від’ємним показником: а) 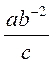 ; б)
; б) 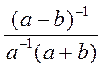 ; в)
; в) 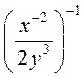 ; г)
; г) 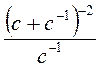 .
.
VI. Підсумки уроку
Самостійна робота № 7
Варіант 1 | Варіант 2 |
Функцію задано формулою | |
|
|
А) Знайдіть значення функції при значенні аргументу: -2; 4. Б) При якому значенні аргументу функція дорівнює -4; -16? В) Які з точок А(-0,5; 32); В(32; 0,5); С Г) Побудуйте графік функції. Д) За допомогою побудованого графіка розв’яжіть рівняння: | |
|
|
VII. Домашнє завдання
1. Повторити матеріал розділу “Степінь з цілим від’ємним показником та його властивості”; виписати назви основних понять теми.
2. Розв’язати вправи іншого варіанта самостійної роботи № 7, виконати аналіз помилок, яких припустились у класі.
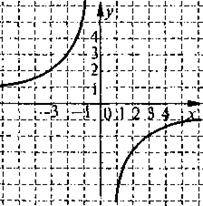
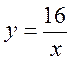
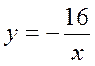
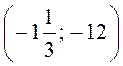 ; D
; D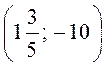 Належать графіку функції?
Належать графіку функції?