ГАРМОНІЧНІ КОЛИВАННЯ
МЕХАНІЧНІ І ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ
Розділ 3 Коливання і хвилі
§ 21.ГАРМОНІЧНІ КОЛИВАННЯ
Серед усіх різноманітних форм коливань важливе місце належить гармонічним коливанням. Гармонічні коливання – це найпростіші періодичні коливання. Більшість коливань, які трапляються на практиці, складні. З курсу математики відомо, що будь-яке складне періодичне коливання є сумою найпростіших гармонічних коливань (гармонік). Гармонічні коливання – єдиний тип коливань, форма яких не спотворюеться_у процесі відтворення. Коливання,
Переконаємося в цьому за допомогою коливання кульки, яка ковзає вздовж осі Ох, під дією сили пружності пружини F = – kx.
Коливання кульки можна розглядати як проекцію колового руху кульки (мал. 100) на вісь Ох. Нехай А – рухомий радіус допоміжного кола, що відповідає найбільшому відхиленню кульки від положення рівноваги Хщах. Якщо обертати кульку по колу з такою кутовою швидкістю со0, щоб проекція її руху збігалася з рухом кульки під дією сили пружності пружини, то її миттєве положення буде визначатися
Під час обертання рухомого радіуса зі сталою кутовою швидкістю СО0 кут ф між радіусом і віссю Ох зростає прямо пропорційно часу:
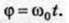
Проекція х рухомого радіуса на вісь Ох змінюватиметься за законом:
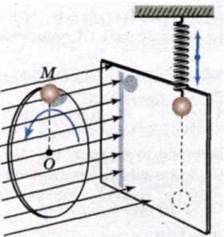
Аналогічно можна також порівняти коливання тіні кульки, закріпленої на
Мал. 100
Мал. 101
Мал. 102
Диску, який обертається зі сталою кутовою швидкістю ш0, і кульки пружинного маятника (мал. 101). Можна підібрати таку швидкість обертання диска, що рух тіні кульки на екрані повністю збігатиметься з рухом кульки пружинного маятника. Так само можна показати, що проекція рухомого радіуса диска ОМ на вертикальний діаметр змінюватиметься за законом:
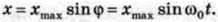
Проекції рухомого радіуса в обох описаних випадках можна розглядати як координати кульки, яка обертається по колу.
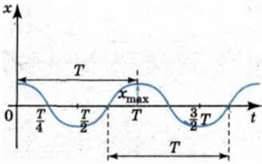
Таким чином, у зазначених випадках координата тіла, яке здійснює вільні коливання, змінюється з часом за законом синуса або косинуса. Графік залежності координати тіла від часу відповідно до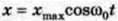 
Є косинусоїда, зображена на мал. 102.
Важливою характеристикою коливального руху є амплітуда. Амплітудою гармонічних коливань називають модуль найбільшого зміщення тіла (коливальної системи) від положення рівноваги.
Амплітуда може мати різні значення залежно від того, наскільки ми зміщуємо тіло від положення рівноваги в початковий момент часу, і від того, яка швидкість надається при цьому тілу. Іншими словами, амплітуда визначається початковими умовами і дорівнює множнику при синусоїдальній чи косинусоїдальній функції, який відповідає даному коливальному процесу.
Через інтервал часу, що дорівнює періоду Т, тобто зі збільшенням аргументу косинуса на ω0T. рух повторюється і косинус набуває попереднього значення. Проте з математики відомо, що найменший період косинуса дорівнює 2∏. Отже, ω0 Т = 2∏, звідки
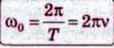
Таким чином, величина ω0 – це кількість коливань тіла, але не за одну секунду, а за 2я секунд. Вона називається циклічною або коловою частотою.
При заданій амплітуді гармонічних коливань координата коливного тіла в будь-який момент часу однозначно визначається аргументом косинуса (або синуса) φ = ω0t. Величину <р, яка стоїть під знаком косинуса або синуса, називають фазою коливань, що описуються цими функціями. Одиницею фази є радіан або градус.
Від фази залежить значення не лише координати, а й швидкості, й прискорення, що змінюються також за гармонічним законом. Тому можна сказати, що при заданій амплітуді фаза визначає стан коливальної системи у будь-який момент часу.
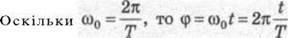
Відношенняn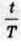
показує, яка частина періоду пройшла від початку коливань.
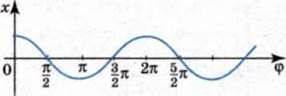
Мал. 103
Будь-якому значенню часу, вираженому в частинах періоду, відповідає значення фази, виражене в радіанах.
Наприклад, коли пройде час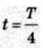 
(чверть періоду),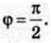 
На графіку можна зобразити залежність координати коливної точки не від часу, а від фази. На мал. 103 показано ту саму косинусоїду, що й на мал. 102, але на горизонтальній осі замість часу відкладено різні значення фази <р.
Вам вже відомо, що для гармонічних коливань координата тіла змінюється з часом відповідно до закону косинуса або синуса. Проте при цьому слід врахувати поняття фази.
Синус відрізняється від косинуса лише зсувом аргументу на чверть періоду, тобто на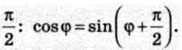 
Тому для опису гармонічних коливань замість формули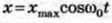 
можна використати формулу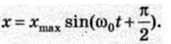 
Проте при цьому початкова фаза, тобто значення фази в момент t = 0, дорівнюватиме не нулю, а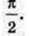 
Звичайно коливання тіла на пружині (або маятнику) збуджують, виводячи його з положення рівноваги, а потім відпускаючи. У початковий момент зміщення від положення рівноваги є максимальне, тому описувати коливання зручніше формулою 
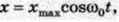використовуючи косинус.
Інша річ, коли коливання тіла, що перебуває у стані спокою, збуджують короткочасним поштовхом. Тоді в початковий момент координата дорівнює нулю, і коливання зручніше описувати формулою з використанням синуса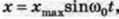 
тому що при цьому початкова фаза дорівнює нулю.
Коливання, описані рівняннями
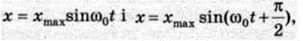
Різняться між собою лише фазами. Різниця фаз (зсув фаз) цих коливань дорівнює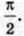 
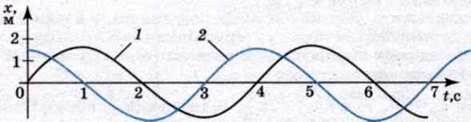
На мал. 104 показано графіки залежності координат від часу для
Мал. 104
Мал. 105
Двох гармонічних коливань, зсунутих за фазою на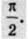 
Графік 1 відповідає коливанням, що відбуваються відповідно до закону синусоїди х = хm&p;х sin(0,£,а графік 2 – коливанням, що відбуваються відповідно до закону косинусоїди
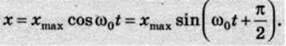
Щоб визначити різницю фаз двох коливань, обидва ці коливання треба записати через одну і ту саму тригонометричну функцію (косинус або синус).
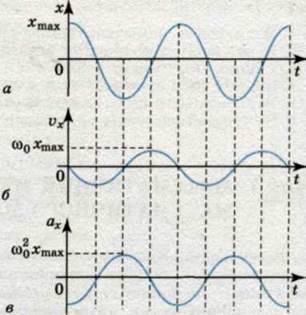
У гармонічних коливаннях координати тіла, його швидкість і прискорення також змінюються гармонічно. Проекція швидкості на вісь Ох має такий вигляд:
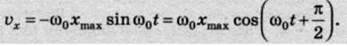
Швидкість під час гармонічних коливань змінюється з часом гармонічно, але коливання швидкості випереджають за фазою коливання координати на 
У момент, коли координата дорівнює нулю (момент проходження положення рівноваги), модуль швидкості максимальний, і, навпаки, швидкість дорівнює нулю, коли координата максимальна за модулем (мал. 105, а, б). Максимальне значення швидкості за модулем, тобто амплітуду vmax коливань швидкості можна записати через амплітуду зміщення у вигляді
Проекція прискорення на вісь Ох така:
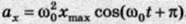
Під час гармонічних коливань прискорення змінюється гармонічно. Амплітуда прискорення
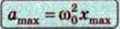
За фазою коливання прискорення випереджають коливання координати на ∏.
Прискорення і координата за модулем набувають максимального значення одночасно, але мають протилежні знаки. У такому разі кажуть, що коливання відбуваються у протифазі (мал. 105, а, в).
(1 votes, average: 5.00 out of 5)
Loading...