Головна ⇒ 📌Довідник з математики ⇒ Геометрична прогресія
Геометрична прогресія
Математика – Алгебра
Послідовності
Геометрична прогресія
Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії.
Формула n-го члена геометричної прогресії:
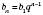 .
.
Теорема. Послідовність тоді й тільки тоді є геометричною прогресією, якщо кожний її член, починаючи з другого, є середнім геометричним
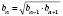
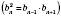 . (**)
. (**)Формула суми n перших членів геометричної прогресії:
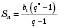 , якщо
, якщо 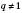 ,
,або
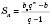 , якщо
, якщо 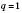 ,
, 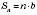 .
.Формула суми нескінченної геометричної прогресії:
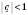 ;
; 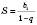 .
.Для розв’язання більшості задач на арифметичну й геометричну прогресії, а також комбінованих задач на прогресії зручно діяти так: усі дані задачі на арифметичну прогресію виразити через a1 і d (на геометричну – через b1 і q) і скласти рівняння або систему рівнянь за умовою задачі (або використовуючи властивості (*) і (**)).
Related posts:
- Геометрична прогресія. Формула n-го члена геометричної прогресії УРОК № 55 Тема. Геометрична прогресія. Формула n-го члена геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед інших числових послідовностей, відшукувати знаменник геометричної прогресії, перші кілька членів […]...
- Геометрична прогресія УРОК № 54 Тема. Геометрична прогресія Мета уроку: домогтися засвоєння учнями: означення геометричної прогресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивостей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Арифметична прогресія. Формула n-го члена арифметичної прогресії УРОК № 51 Тема. Арифметична прогресія. Формула n – го члена арифметичної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять арифметичної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена арифметичної прогресії. Закріпити вміння: вирізняти арифметичну прогресію серед числових послідовностей, відшукувати різницю арифметичної прогресії, перші члени […]...
- Сума перших n членів геометричної прогресії УРОК № 57 Тема. Сума перших n членів геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед числових послідовностей, відшукувати знаменник геометричної прогресії, перші члени геометричної прогресії, а […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Сума перших n членів арифметичної прогресії УРОК № 53 Тема. Сума перших n членів арифметичної прогресії Мета уроку: закріпити знання учнів про формули обчислення суми перших n членів арифметичної прогресії, а також про її означення та властивості, вивчені на попередніх уроках; сформувати уявлення про спосіб розв’язування задач на відшукання суми послідовних членів арифметичної прогресії з n-го по т-й включно (n < […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Геометрична ізомерія – Типи ізомерії ІЗОМЕРІЯ ОРГАНІЧНИХ РЕЧОВИН 2. Типи ізомерії 2.5 . Геометрична ізомерія У карбонових ланцюгах, в яких між атомами Карбону є тільки одинарний зв’язок (С-С), атоми можуть вільно обертатися довкола своєї осі зв’язку. Отже, немає різниці між формами Або між Якщо карбоновий ланцюг з двох або більше атомів Карбону містить подвійний зв’язок, то атоми Карбону біля подвійного […]...
- Закони геометричної оптики – ГЕОМЕТРИЧНА ОПТИКА Формули й таблиці ФІЗИКА ГЕОМЕТРИЧНА ОПТИКА Закони геометричної оптики Закон відбиття α = γ α – кут падіння; γ – кут відбиття; – перпендикуляр до границь розділу двох середовищ. Закон заломлення β – кут заломлення. Відносний показник заломлення N21 – відносний показник заломлення; υ1, υ2- швидкість світла в даних середовищах, . Абсолютний показник заломлення N21 […]...
- Формули скороченого множення Математика – Алгебра Многочлен Формули скороченого множення – Формула різниці квадратів. Добуток різниці двох виразів і їх суми дорівнює різниці квадратів цих виразів. – Формула квадрата суми. Квадрат суми двох виразів дорівнює квадрату першого виразу плюс подвоєний добуток цих виразів і плюс квадрат другого виразу. – Формула квадрата різниці. Квадрат різниці двох виразів дорівнює квадрату […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- ХВИЛЬОВА ТА ГЕОМЕТРИЧНА ОПТИКА Вправа 25 1. Дано: D1 = S1O D2= S2O Δ – ? Розв’язання: Максимум освітленості від когерентних джерел світла спостерігається, якщо геометрична різниця ходу дорівнює цілому числу довжини хвиль: Δ = d2- d1= kλ. Оскільки S1O = S2O, το Δ = S2O – S1O = 0, k = 0. В точці О буде спостерігатися максимум […]...
- СФЕРИЧНІ ДЗЕРКАЛА – ГЕОМЕТРИЧНА ОПТИКА Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 6. ОПТИКА 6.2. ГЕОМЕТРИЧНА ОПТИКА 6.2.7. СФЕРИЧНІ ДЗЕРКАЛА Увігнуте дзеркало – збирає пучок світла після відбивання, опукле – розсіює. Формула сферичного дзеркала: Рівняння спряжених точок і зображення предмета у сферичних дзеркалах за умови параксіальності променів такі самі, як для сферичних лінз. Промінь, який падає в […]...
- ХІД ПРОМЕНІВ ЧЕРЕЗ ПЛОСКОПАРАЛЕЛЬНУ ПЛАСТИНКУ, ПРИЗМУ – ГЕОМЕТРИЧНА ОПТИКА Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 6. ОПТИКА 6.2. ГЕОМЕТРИЧНА ОПТИКА 6.2.4. ХІД ПРОМЕНІВ ЧЕРЕЗ ПЛОСКОПАРАЛЕЛЬНУ ПЛАСТИНКУ, ПРИЗМУ Хід променів у плоскопаралельній пластинці Після проходження через плоскопаралельну пластинку промені виходять під тим самим кутом, під яким вони на неї падають. При цьому пластинка зміщує промінь світла паралельно йому самому на відстань […]...
- ЗАКОНИ ВІДБИВАННЯ СВІТЛА – ГЕОМЕТРИЧНА ОПТИКА Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 6. ОПТИКА 6.2. ГЕОМЕТРИЧНА ОПТИКА 6.2.2. ЗАКОНИ ВІДБИВАННЯ СВІТЛА 1. Падаючий і відбитий промені та перпендикуляр, опущений у точку падіння, лежать в одній площині. 2. Кут відбивання дорівнює куту падіння: α = β (рис. 42). Рис. 42 Наслідок: промінь відбитий і падаючий взаємно обернені. Дзеркальне […]...
- Арифметичні дії додавання і віднімання Арифметичні дії додавання і віднімання 1 Обчисли. 2 Згадай закони додавання; правила додавання і віднімання. Визнач без обчислень істинність або хибність поданих рівностей. Поясни свої міркування. 5 867 – (1 329 + 2 867) = (5 867 – 2 867) – 1 329 (32 405 + 16 000) + 14 000 = 32 405 + […]...
- Задачі на знаходження четвертого пропорційного Мета: узагальнити математичну структуру та способи розв’язування задач на знаходження четвертого пропорційного Тип уроку: узагальнення й систематизації знань і вмінь Дидактичні задачі. Вдосконалювати навички усного позатабличного множення та ділення (РЗ ч. 1 с. 16, №1). Актуалізувати розуміння істотних ознак та двох способів розв’язування задач на знаходження четвертого пропорційного; узагальнити знання про математичну структуру задач на […]...
- Письмове множення на трицифрове число Письмове множення на трицифрове число 1 Обчисли. 2 Виконай множення письмово з коментарем. 724 ∙ 326 157 ∙ 629 645 ∙ 217 918 ∙ 582 3 Поясни розв’язання. 4 Знайди значення добутків, виконай перевірку. 347 ∙ 409 4 468 ∙ 308 528 ∙ 207 2493 ∙ 105 292 ∙ 803 1256 ∙ 206 5 Кріт […]...
- Задачі на подвійне зведення до одиниці Мета: формувати уміння розв’язувати задачі на подвійне зведення до одиниці; формувати навички письмового множення на двоцифрове число. Тип уроку: закріплення та застосування знань, умінь та навичок Дидактичні задачі. Вдосконалювати навички усних обчислень (№1; РЗ ч. 1 с. 27, №1). Зіставити задачі на подвійне зведення до одиниці різного рівня складності ( №1); розвивати уміння розв’язувати прямі […]...
- ДІЯ ВІДНІМАННЯ. ПРАВИЛО ВІДНІМАННЯ СУМИ ВІД ЧИСЛА. ТАБЛИЧНЕ Й ПОЗАТАБЛИЧНЕ, УСНЕ І ПИСЬМОВЕ ВІДНІМАННЯ. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ ВІДНІМАННЯМ Мета: узагальнити уявлення учнів про дію віднімання; закріпити вміння розв’язувати задачі на віднімання; повторити прийоми письмового віднімання трицифрових чисел; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Гра “Хто швидше?” 1-ша група 2-га група 3-тя група 3. Математичний диктант […]...
- ОКО ЯК ОПТИЧНА СИСТЕМА – ГЕОМЕТРИЧНА ОПТИКА Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 6. ОПТИКА 6.2. ГЕОМЕТРИЧНА ОПТИКА 6.2.5. ОКО ЯК ОПТИЧНА СИСТЕМА Око являє собою оптичну систему, яка дає зображення на світочутливій сітчастій оболонці очного яблука – сітківці. Око як оптичний прилад складається з чотирьох лінз (рис. 21): 1) рогова оболонка 1 – основна за оптичною силою […]...
- Одиниці вимірювання площі. Прості і складені задачі, які включають дії над величинами, вираженими одиницями площі (№№ 602-608) Тема. Одиниці вимірювання площі. Прості і складені задачі, які включають дії над величинами, вираженими одиницями площі (№№ 602-608). Мета. Ознайомити учнів із одиницями вимірювання площі: 1 мм2, 1 см2, 1 дм2, 1 м2, 1 а, 1 га, 1 км2; вправляти учнів у розв’язуванні простих і складених задач, які включають дії над величинами, вираженими одиницями площі; […]...
- Круг. Площа круга Урок № 5 7 Тема. Круг. Площа круга Мета: сформувати уявлення учнів про геометричну фігуру круг та поняття площі круга; навчити користуватися формулою S = nR2 для розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Запишіть формулу, за якою обчислюється довжина кола, […]...
- Множення вектора на число УРОК № 47 Тема. Множення вектора на число Мета уроку: формування вміння множити вектор на число; вивчення властивостей множення вектора на число; формування вмінь застосовувати вивчені значення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині”[13]. Вимоги до рівня підготовки учнів: описують множення вектора на число; […]...
- Ділення на дфоцифрове число Мета: формувати навички письмового ділення на двоцифрове число Тип уроку: закріплення та застосування знань, умінь та навичок Дидактичні задачі. Вдосконалювати навички усних обчислень ( РЗ ч. 1 с. 31, №1). Актуалізувати вміння визначати розрядний склад чисел ( №1); виконувати прийом письмового ділення на двоцифрове число у випадку, коли значення частки записується двома цифрами; застосовувати спосіб […]...