Геометрична прогресія. Формула n-го члена геометричної прогресії
УРОК № 55
Тема. Геометрична прогресія. Формула n-го члена геометричної прогресії
Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед інших числових послідовностей, відшукувати знаменник геометричної прогресії, перші кілька членів геометричної прогресії, а також використовувати властивості геометричної прогресії. Сформувати
Тип уроку: доповнення і закріплення знань, відпрацювання вмінь та навичок.
Наочність та обладнання: опорний конспект № 34.
Хід уроку
I. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Перевірка домашнього завдання
Для усвідомленої роботи учнів на цьому етапі уроку можна провести перевірку домашнього завдання за зразком.
Інший варіант проведення цього етапу уроку – виконання тестових завдань (див. нижче)
Тестові завдання
1. Яка з наведених послідовностей є геометричною прогресією?
а) 2; 6; 18; 54;
Б) 80; 40; 20; 5;
В) 4; 8; 32; 64;
Г) 2; -10; 50; 250.
2. Знайдіть знаменник геометричної прогресії (bn), якщо b5 = 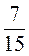 , b6 =
, b6 = 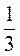 .
.
А) 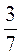 ; б)
; б) 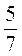 ; в)
; в) 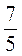 ; г)
; г) 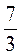 .
.
3. Дев’ятий член геометричної прогресії дорівнює 12, а знаменник дорівнює 3. Знайдіть десятий член геометричної прогресії.
А) 15; б) 36; в) 39; г) 108.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Так само, як при вивченні питання про формулу п-го члена арифметичної прогресії, роботу на цьому етапі уроку організуємо як колективний пошук розв’язання задачі: як найраціональнішим способом знайти значення n-го члена геометричної прогресії, знаючи її перший член і знаменник.
Усвідомивши нераціональність розв’язування задачі відомим учням способом (через застосування рекурентної формули), вони приходять до запитання: чи не існує способу знаходження будь-якого члена геометричної прогресії без необхідності знаходити попередні кілька її членів? Пошук відповіді на це запитання – основна мета уроку.
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. Чи є геометричною прогресією послідовність (хn):
1) 3; 3; 3; 3; 3;
2) 0; 0; 0; 0; 0;
3) 3; 6; 12; 24; 48.
2. Назвіть перший, третій та п’ятий члени послідовності, заданої формулою хn = 64 • 21-n. Чи є вона геометричною прогресією? Чому дорівнює її знаменник?
3. Відомо, що числа а1; а2; а3; а4; а5 утворюють геометричну прогресію зі знаменником b. Чи буде геометричною прогресією послідовність:
1) 2a1; 2а2; 2а3; 2а4; 2а5;
2) а1; а3; а5?
Чому дорівнює знаменник кожної з цих прогресій?
V. Доповнення знань
План вивчення нового матеріалу
1. Формула n-го члена геометричної прогресії.
2. Приклади застосування виведеної формули.
Опорний конспект № 34
Формула n-го члена геометричної прогресії |
Якщо (bn) – геометрична прогресія, то bn=bl – qn-1, Де b1 – перший член геометричної прогресії; Q – знаменник геометричної прогресії. |
Приклад 1. Знайдемо шостий член геометричної прогресії (b1): Розв’язання B1 = Відповідь: 625. |
Приклад 2. Знайдемо перший член геометричної прогресії (bn), якщо b7 = 32; q = -2. Розв’язання B7 = b1 • q6 Відповідь: |
Приклад 3. Знайдемо знаменник геометричної прогресії (bn), у якої b7 = -12, b9 = -108. Розв’язання B9 = b1 • q8; b7 = b1• q6 Відповідь: 3 або -3. |
Методичний коментар
Єдиний новий момент, який додається до вивчених на попередньому уроці означення та властивостей геометричної прогресії – це формула n-го члена геометричної прогресії, яка виводиться через означення, і сама надалі буде основою для виведення формули суми перших п членів геометричної прогресії (слід зазначити, що спосіб міркувань, які проводяться для отримання названої в темі уроку формули, є традиційним, так само, як і основні типи задач на її застосування,- див. нижче). Приблизний зміст навчального матеріалу вміщено в опорному конспект № 34.
VI. Відпрацювання вмінь
Письмові вправи
Зміст письмових вправ уроку може бути таким:
1) задачі на пряме застосування формули n-го члена геометричної прогресії, у якої задано перший член та знаменник або яка задана переліком перших кількох своїх членів;
2) знайти n-й член, якщо відомі кілька перших членів геометричної прогресії;
3) знайти номер деякого члена геометричної прогресії або перевірити, чи є дане число членом даної геометричної прогресії;
4) прикладні задачі на застосування означення геометричної прогресії та формули її n-го члена.
Методичний коментар
Зміст вправ та мета їх розв’язування такі самі, як і на попередньому уроці: закріплення означення та формули, вивчених на цих уроках, а також вироблення оперативних умінь із застосування формул при розв’язуванні задач у різних ситуаціях (якщо дозволяють успіхи учнів, підвищується рівень складності задач за рахунок задач на застосування властивостей геометричної прогресії). Серед задач уроку досить важливе місце мають посідати здачі на складання систем рівнянь вищих степенів (якщо дозволяє рівень математичної підготовки учнів), а також задачі на застосування характеристичної властивості геометричної прогресії.
VII. Підсумки уроку
Контрольні запитання
1. Як знайти знаменник геометричної прогресії, якщо відомі її перший і другий члени?
2. Як знайти третій член геометричної прогресії, якщо відомі її перший і другий члени?
3. Як знайти шостий член геометричної прогресії, якщо відомі її перший член і знаменник?
VIII. Домашнє завдання
1. Вивчити зміст матеріалу в опорних конспектах № 33, 34.
2. Виконати самостійну роботу (див. нижче) за варіантом, указаним учителем.
Самостійна робота
Варіант 1
Розв’яжіть задачу.
1. Знайдіть перші чотири члени геометричної прогресії (bп), якщо b1 = -2, q = -3.
2. Знайдіть знаменник і 5-й член геометричної прогресії 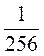 ;
; 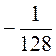 ,
, 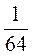 , … .
, … .
3. Між числами 16 і 81 вставте три таких числа, щоб разом із даними числами вони утворювали геометричну прогресію.
4. Знайдіть перший член і знаменник геометричної прогресії (bn), якщо b10 = 9b8, b3 + b6 = 168, (q > 0).
Варіант 2
Розв’яжіть задачу.
1. Знайдіть перші чотири члени геометричної прогресії (bn), якщо b1 = 25, q = -0,2.
2. Знайдіть знаменник і 5-й член геометричної прогресії -72; 12; -2; … .
3. Між числами 64 і 27 вставте два таких числа, щоб разом із даними числами вони утворювали геометричну прогресію.
4. Знайдіть перший член і знаменник геометричної прогресії (bn), якщо b10 = 25b8, b2 + b4 = -520 (q > 0).
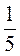 ; 1; 5; … .
; 1; 5; … .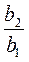 = 5; b6 = b1 • q5 =
= 5; b6 = b1 • q5 = 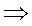 b1 =
b1 = 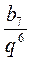 =
= 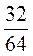 =
= 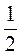 .
.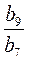 = q2; q2 =
= q2; q2 = 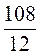 = 9, тоді q = 3 або q = -3.
= 9, тоді q = 3 або q = -3.