Головна ⇒ 📌Математика ⇒ ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ

&22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок абсциса – це значення змінної х, а ордината – відповідне значення змінної у. Відтак дістанемо графік рівняння з двома змінними.

Запам’ятайте!

Графіком рівняння

з двомa змінними називається зображення на координатній площині всіх точок, координати яких задовольняють дане рівняння.

Подивіться на малюнки 64 і 65. Ви бачите графік рівняння 0,5x – у = 2, де х – парне одноцифрове число (мал. 64), і графік рівняння х2 + у2 = 4 (мал. 65). Перший графік містить усього чотири точки, оскільки змінні х і у можуть набувати лише по чотири відповідні значення. Другий же графік є лінією на координатній площині. Він містить безліч точок, оскільки змінна х може набувати будь-яких значень від -2 до 2 і таких чисел – безліч. Відповідних значень у теж безліч. Вони змінюються від – 2 до 2.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

class=""/>

Мал. 64

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

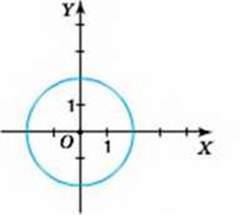
Мал. 65

На малюнку 66 зображено графік рівняння х + у = 4. На відміну від графіка рівняння х2 + у2 = 4 (див. мал. 65), кожній абсцисі точок даного графіка відповідає єдина ордината. А це означає, що на малюнку 66 зображено графік функції. Переконайтеся самостійно, що графік рівняння на малюнку 64 також є графіком функції.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

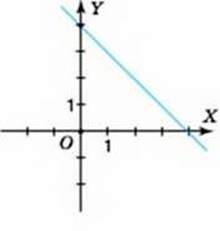
Мал. 66

Зверніть увагу

Не в кожного рівняння його графік є графіком функції, проте кожен графік функції є графіком деякого рівняння.

Рівняння x + y = 4 є лінійним рівнянням із двома змінними. Розв’язавши його відносно у, дістанемо: у = – х + 4. Отриману рівність можна розуміти як формулу, що задає лінійну функцію у = – х + 4. Графіком такої функції є пряма. Отже, графіком лінійного рівняння х + у = 4, який зображено на малюнку 66, є пряма.

? Чи можна стверджувати, що графік будь-якого лінійного рівняння з двома змінними є прямою? Ні. Наприклад, лінійне рівняння 0 ∙ х + 0 ∙ у = 0 задовольняє будь-яка пара чисел, а тому графік цього рівняння містить усі точки координатної площини.

З’ясуємо, що є графіком лінійного рівняння з двома змінними aх + bу + с = 0 , залежно від значень коефіцієнтів а, b і с. Можливими є такі випадки.

Нехай a ≠ 0, , b ≠ 0, с ≠ 0. Тоді рівняння ах + by + с = 0 можна подати у вигляді:

1. y = 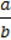ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИX – ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ.

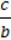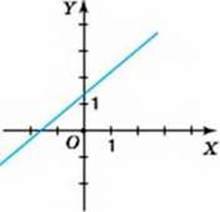
Дістали рівність, що задає лінійну функцію у(х). Її графіком, а значить, і графіком даного рівняння, є пряма, що не проходить через початок координат (мал. 67).

2. Нехай а ≠ 0, b ≠ 0, с = 0. Тоді рівняння ах + by + с = 0 набуває вигляду ах + by + 0 = 0, або у = 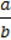ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИХ.

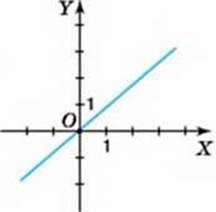
Дістали рівність, що задає пряму пропорційність у(х). Її графіком, а значить, і графіком даного рівняння, є пряма, що проходить через початок координат (мал. 68).

3. Нехай a ≠ 0, b = 0, с ≠ 0. Тоді рівняння ах + by + с = 0 набуває вигляду ах + 0 ∙ у + с = 0, або х = –ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Maл. 67

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Мал. 68

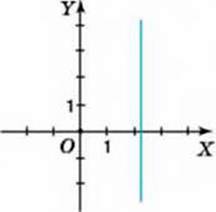
Дістали рівність, що не задає функцію y(). Цю рівність задовольняють такі пари чисел (х; у), у яких х = ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ, а у – будь-яке число. На координатній площині ці точки лежать на прямій, паралельній осі OY. Отже, графіком даного рівняння є пряма, паралельна осі ординат (мал. 69).

4. Нехай a ≠ 0, b = 0, с = 0. Тоді рівняння ах + by + с = 0 набуває вигляду ах + 0 ∙ у + 0 = 0, або х = 0.

Цю рівність задовольняють такі пари чисел (x; у), у яких х = 0, а у – будь-яке число. На координатній площині ці точки лежать на осі OY. Отже, графіком даного рівняння с пряма, що збігається з віссю ординат.

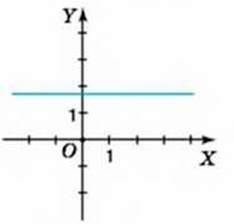
5. Нехай а ≠ 0, b ≠ 0, с ≠0. Тоді рівняння ах + bу + с = 0 набуває виглядy 0 ∙ х + by + с = 0, або у = –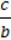ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ. Ця рівність задає функцію y(x), що набуває тих самих значень для будь-яких значень x, тобто є сталою. Її графіком, а значить, і графіком даного рівняння, є пряма, паралельна осі абсцис (мал. 70).

6. Нехай а = 0, b ≠ 0, с = 0. Тоді рівняння ах + by + с = 0 набуває вигляду 0 ∙ х + by + 0 = 0, або у = 0. Отримали сталу функцію у(х), у якої кожна точка графіка лежить на осі ОХ. Отже, графіком даного рівняння є пряма, що збігається з віссю абсцис.

7. Нехай a = 0, b = 0, с ≠ 0. Тоді рівняння ах + by + с = 0 набуває вигляду 0 ∙ х + 0 ∙ у + с = 0, або 0 ∙ х + 0 ∙ у = с. А таке лінійне рівняння не має розв’язків, тому його графік не містить жодної точки координатної площини.

8. Нехай а = 0, b = 0, с = 0. Тоді рівняння ах + by + с = 0 набуває вигляду 0 ∙ х + 0 ∙ y + 0 = 0, або 0 ∙ x + 0 ∙ у = 0. А таке лінійне рівняння має безліч розв’язків, тому його графіком с вся координатна площина.

Можемо підсумувати отримані результати.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Мал. 69

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Мал. 70

Графік лінійного рівняння з двома змінними ах + bу +с = 0:

– є прямою, якщо або а ≠ 0, або b ≠ 0;

– є всією площиною, якщо а = 0, b = 0 і с = 0;

– не містить жодної точки координатної площини, якщо а = 0, b = 0 і с ≠ 0.

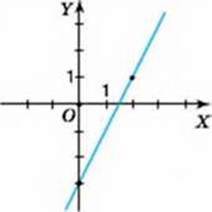
Задача. Побудуйте графік рівняння 2х – у – 3 = 0

Розв’язання. Рівняння 2х – у – 3 = 0 є лінійним. Тому його графіком є пряма у = 2х – 3. Для її побудови достатньо задати дві точки, що належать цій прямій. Складемо таблицю значень у для двох довільних значень х, наприклад, для х = 0 і х = 2(табл. 27).

Таблиця 27

X

0

2

Y

-3

1

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Мал. 71

На координатній площині позначимо точки з координатами (0; -3) і (2; 1) та проведемо через них пряму (мал. 70). Ця пряма – шуканий графік рівняння 2х – у – 3 = 0.

? Чи можна ототожнювати графік лінійного рівняння з двома змінними і графік рівняння першого степеня з двома змінними? Ні, оскільки існують лінійні рівняння, що не є рівняннями першого степеня. Наприклад, такими є рівняння 0 ∙ х + 0 ∙ у + с = 0 і 0 ∙ х + 0 ∙ у + 0 = 0.

Зверніть увагу:

– графік лінійного рівняння з двома змінними може бути прямою, всією площиною або не містити жодної точки координатної площини;

– графік рівняння першого степеня з двома змінними завжди є прямою.

Дізнайтеся більше

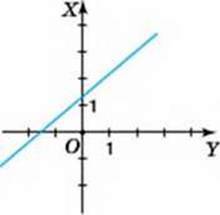
1. Нехай а ≠ 0. Тоді загальний розв’язок рівняння можна подати ще й у такому вигляді: Х = –ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ у –ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ. Дістали лінійну функцію х(у). Її графіком є пряма. Для побудови такого графіка треба по-іншому упорядкувати осі координат: першою координатною віссю (незалежної змінної) вважати вісь ОУ, а другою (залежної змінної)

– вісь ОХ. Тоді вісь ОY зручно розташувати горизонтально, а вісь ОХ

– вертикально (мал. 72). Графік рівняння у цьому випадку теж буде по-різному розміщуватися на координатній площині, залежно відзначень коефіцієнтів b і с. Дослідіть це самостійно.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

Мал. 72

2. Микола Миколайович Боголюбов (1909-1992) – видатний вітчизняний математик і механік, фізик-теоретик, засновник наукових шкіл з нелінійної механіки і теоретичної фізики, академік АН УРСР (від 1948) і АН СРСР (від 1953). Народився в м. Нижній Новгород Російської імперії. У 1921 р. сім’я переїхала до Києва. Після закінчення семирічної школи Боголюбов самостійно вивчав фізику та математику і з 14-ти років уже брав участь у семінарі кафедри математичної фізики Київського університету під керівництвом академіка Д. О. Граве. У 1924 р. в 15-річному віці Боголюбов написав першу наукову працю, а наступного року був прийнятий до аспірантури АНУРСР до академікам. М. Крилова, яку закінчив у 1929 р., отримавши у 20 років ступінь доктора математичних наук.

У 1929 p. М. М. Боголюбов став науковим співробітником Української академії наук, у 1934 почав викладати в Київському університеті (від 1936 р. – професор). Із кінця 40-х років XX ст. одночасно працював у Росії. Був директором Об’єднаного інституту ядерних досліджень, а згодом – директором Математичного інституту імені В. А. Стєклова в Москві, викладав у Московському державному університеті імені Михайла Ломоносова. У 1966 р. став першим директором створеного ним Інституту теоретичної фізики АН УРСР у Києві, одночасно (1963-1988) він – академік – секретар Відділу математики АН СРСР.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

М. М. Боголюбов – двічі Герой Соціалістичної Праці (1969,1979), нагороджений Ленінською премією (1958), Державною премією СРСР (1947.1953,1984), Золотою медаллю ім. М. В. Ломоносова АН СРСР (1985).

21 вересня 2009 р. на фасаді Червоного корпусу Київського національного університету імені Тараса Шевченка була відкрита меморіальна дошка геніальному вченому-академіку Миколі Боголюбову на честь століття від дня його народження.

У 1992 р. Національною академією наук України була заснована Премія НАН України імені М. М. Боголюбова, яка вручається Відділенням математики НАН України за видатні наукові роботи в галузі математики і теоретичної фізики. На честь вченого була названа мала планета “22616 Боголюбов”.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Що є графіком лінійного рівняння з двома змінними?

2. У якому випадку графіком рівняння з двома змінними є пряма; площина?

3. У якому випадку графік лінійного рівняння з двома змінними проходить через початок координат?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

1078. На якому з малюнків 73-74 зображено графік лінійного рівняння з двома змінними? Відповідь поясніть.

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

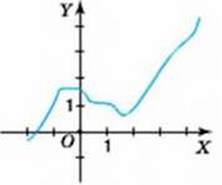
Мал. 73

ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ

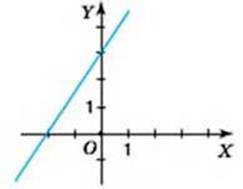
Мал. 74

1079. За яких значень коефіцієнтів а, b і с пряма ах + bу + с =0.

1) проходить через початок координат;

2) паралельна осі абсцис;

3) паралельна осі ординат;

4) збігається з віссю абсцис;

5) збігається з віссю ординат?

1080. Не виконуючи побудови, з’ясуйте, чи належить графіку лінійного рівняння з двома змінними 6х – 2у + 1 = 0 точка:

1)А(-1;2,5); 2)В(0;3,5); 3) С(-2; 5,5); 4)D(1,5;5).

1081. Не виконуючи побудови, з’ясуйте, чи належить графіку лінійного рівняння з двома змінними 3х + 3у – 5 = 0 точка:

1) A (-1; ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ); 2) B (0; 1ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ).

1082. Для даного лінійного рівняння з двома змінними знайдіть значення у, що відповідає заданому значенню х:

1) 2х + у – 4 = 0, якщо х = 0; 3) 3х + 3у – 1 = 0, якщо х = 2;

2) 4х – 2y + 5 = 0, якщо х = 0; 4)-5х – у + 6 = 0, якщо х = 2.

1083. Для даного лінійного рівняння з двома змінними знайдіть значення у, що відповідає заданому значенню х:

1)3х – у + 2 = 0, якщо х = 0; 2) 6х – 5y – 7 = 0, якщо х = 2.

1084. Побудуйте графік лінійного рівняння з двома змінними:

1) 2х + у – 4 = 0; 4) – х + 2у + 8 = 0; 7) 5х – 10 = 0;

2) 6х – 2y + 12 = 0; 5)-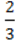ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИХ – 2у + 4 = 0; 8)-2у + 4 = 0;

3) 5х – 10y = 0; 6)х – ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИУ = 0; 9) х – у = 0.

1085. Побудуйте графік лінійного рівняння з двома змінними:

1) 4х + у – 3 = 0; 4) 10х – 5у – 1ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ = 0;

2) 9х – 3у + 12 = 0; 5) 2х + 6 = 0;

3)-4х – 8у = 0; 6) у – 3 = 0.

1086. Знайдіть координати точки перетину графіка лінійного рівняння з двома змінними 2х – 3у – 18 = 0 з віссю:

1) абсцис; 2) ординат.

1087. Знайдіть координати точки перетину графіка лінійного рівняння з двома змінними 5х + 4у – 20 = 0 з віссю:

1) абсцис; 2) ординат.

1088. На прямій, що є графіком рівняння 0,5х + 2у – 4 = 0, позначено точку. Знайдіть ординату цієї точки, якщо її абсциса дорівнює:

1)4; 2)-2.

1089. На прямій, що є графіком рівняння 4х + у – 1 =0, позначено точку, ордината якої дорівнює -3. Знайдіть абсцису цієї точки.

1090. Доведіть, що графіки рівнянь 4х – 3у – 11 = 0, 5х + 2у – 8 = 0 і 0,5х – у – 2 = 0 проходять через точку А (2; -1).

1091. Доведіть, що графіки рівнянь 2x – 5у + 11 = 0 i – x + 2у – 5 = 0 проходять через точку В (-3; 1).

1092. Побудуйте графік рівняння:

1) 2(х + 1) = у + 4;

2) 2(3y – 1,5) – 3(1 – 2х) = 0;

3) (x – y) + 2(x + y) = 5;

4) 3(х – 1) = 4у – 3;

5) 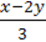ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ = -2;

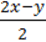6) ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ – 1 = y – 2;

7) х – 4 = 2(у + 0,5х);

8) 2у – х + 2(4х – у) = 6.

1093. Побудуйте графік рівняння:

1) х + 1 = 5(2у – 1);

2) 4(х – 2) = 2 – (y + 10);

3) 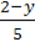ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ = x – 1;

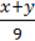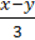4) ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ – ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ = -20;

5) 4(х – у) = 4 – 4у;

6) 7х – 2у = 2(1 + 3,5х).

1094. Графік лінійного рівняння з двома змінними проходить через точку А(3; -2). Знайдіть невідомий коефіцієнт рівняння:

1) ах + 3у – 3 = 0;

2) 2х – by + 8 = 0;

3)-х + 3у – с = 0.

1095. Визначте вид чотирикутника, вершинами якого є точки перетину графіків рівнянь:

Х – y + 4 = 0, х – у – 4 = 0, – х – у + 4 = 0, – х – у – 4 = 0

1096. Побудуйте графік рівняння:

1) а – 4b + 1 = 0; 3) 3a + 0 ∙ b – 12 = 0;

2) 0 ∙ а + 2b + 6 = 0; 4) 0 ∙ a + 0 ∙ b + 5 = 0.

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

1097. Складіть лінійне рівняння з двома змінними за такими даними: 1) 3 кг цукерок і 2 кг печива коштують 120 грн; 2) 2 ручки дорожчі за 5 олівців на 20 грн. Побудуйте графік складеного рівняння.

1098. Побудуйте графік рівняння до задачі про: 1) кількість дівчат і хлопців у вашому класі; 2) покупку зошитів у лінійку й у клітинку.

ЗАДАЧІ НА ПОВТОРЕННЯ

1099. Турист пройшов 12 км за З год. За скільки годин турист подолає відстань 20 км із такою самою швидкістю руху?

1100. Якою має бути швидкість поїзда за новим розкладом, щоб він міг проїхати відстань між двома станціями за 2,5 год, якщо відповідно до старого розкладу, рухаючись зі швидкістю 100 км/год, він долав її за 3 год?


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...

  2. Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...

  3. Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...

  4. Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...

  5. Лінійне рівняння з двома змінними і його графік Урок № 71 Тема. Лінійне рівняння з двома змінними і його графік Мета: вдосконалювати уміння перетворювати лінійні рівняння з двома змінними та знаходити їх розв’язки, а також будувати графіки лінійних рівнянь із двома змінними (залежно від значень а, b, с), працювати з графіками; здійснити діагностику засвоєння основних понять і вмінь, передбачених програмою за темою “Рівняння […]...

  6. Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...

  7. Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...

  8. Рівняння із двома змінними та його розв’язок Урок № 69 Тема. Рівняння із двома змінними та його розв’язок Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати […]...

  9. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &21. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що рівняння можуть бути як з однією змінною, так і з двома змінними. Наприклад, 5(2х + у) = 15 – це рівняння з двома змінними х і у. На відміну від рівняння з однією змінною, рівняння з двома змінними може […]...

  10. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...

  11. Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...

  12. Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...

  13. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...

  14. Лінійне рівняння з двома змінними Розв’яжіть задачі. 1055. 1) 2; 3; -16, вільний член 16; 2) 5; -1; 12; вільний член 12; 3) 1; -2; -1; вільний член -1; 4) 5; -15; вільний член 0. 1056. 1) так; 2) ні; має тільки одну змінну у; 3) так; 4) ні; має тільки одну змінну 1057. 1) -2 – 3 + 5 […]...

  15. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...

  16. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...

  17. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...

  18. Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...

  19. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...

  20. Підсумковий урок з теми “Системи рівнянь з двома змінними” УРОК № 37 Тема. Підсумковий урок з теми “Системи рівнянь з двома змінними” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Системи рівнянь з двома змінними вищих степенів” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. Провести корекційну роботу з метою усунення причин найтиповіших […]...

  21. Розв’язування систем рівнянь з двома змінними УРОК № 33 Тема. Розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про різні способи розв’язування систем рівнянь з двома змінними та випадки їх застосування. Закріпити вміння: за видом системи визначати оптимальний спосіб її розв’язування, описувати дії відповідно до обраного способу розв’язування системи рівнянь з двома змінними, а також виконувати дії відповідно […]...

  22. Рівняння із вдома змінними 870. Рівняння із двома змінними: б) x + 2у = 7; г) х – у = 1; д) 12x + 10у = 0; е) 0x – 2у = 3; ж) 3x + 0у = 0; ж) 0x + 0у = 0; з) 0x + 0y = 1. 871. 2х – у = 3. А) x […]...

  23. Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...

  24. Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...

  25. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &24. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, що систему лінійних рівнянь із двома змінними можна розв’язати графічно. Проте існують інші, більш точні способи розв’язування таких систем – аналітичні способи. У цьому параграфі ви дізнаєтесь про два з них. До аналітичних способів розв’язування […]...

  26. Системи рівнянь з двома змінними УРОК 64 Тема. Системи рівнянь з двома змінними Тестові завдання 1. Яка з пар чисел є розв’язком рівняння 3х2 – 2ху +1 = 0 ? А) (1; 2); б) (2; 2); в) (0; 3); г) (0;0)? 2. Яка з пар чисел є розв’язком системи А) (3; 0); б) (2; 1); в) (1; 2); г) (0; […]...

  27. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...

  28. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...

  29. Системи лінійних рівнянь із двома змінними Урок № 82 Тема. Системи лінійних рівнянь із двома змінними Мета: перевірити рівень опанування учнями навчального матеріалу та вироблених умінь і навичок з теми, передбачених програмою з математики. Тип уроку: контроль засвоєння знань, умінь, навичок. Хід уроку І. Організаційний момент 1. Перевірка готовності до уроку. 2. Зібрати зошити з домашньою контрольною роботою. II. Умова тематичної […]...

  30. Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...

  31. Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...

  32. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...

  33. Лінійна функція Розв’яжіть задачі 882. мал. 40. 883. 1) ні; 2) ні; 3) так. 884. 1) так; 2) ні; 3)так. 885. 1) ні; 2) ні; 3) так. 886. 1) ні; 2) ні; 3) так. 887. 1) ні; 2) ні; 3) так. 888. 1) 4; 2) -6; 3) 2/3. 889. 1) 3; 2) -0,5; 3) %. 890. 1) […]...

  34. Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  35. Лінійна функція, її графік і властивості 849. Лінійною функцією є: 850. Прямою пропорційністю є функції: 851. y = 6x – 5 X -3 -2 -1 0 1 2 3 У -23 -17 -11 -5 1 7 13 852. 1) y = -2x + 5 Якщо x = -4, то у = -2 • (-4) + 5 = 13. Якщо x = […]...

  36. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  37. Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...

  38. Лінійна функція, її графік та властивості Урок № 65 Тема. Лінійна функція, її графік та властивості Мета: ознайомити учнів із “особливими випадками” лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (див. попередній урок) […]...

  39. Розв’язування текстових задач складанням систем рівнянь з двома змінними УРОК № 36 Тема. Розв’язування текстових задач складанням систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про загальну схему розв’язування текстових задач складанням систем рівнянь з двома змінними; доповнити ці знання уявленням про спосіб міркувань при розв’язуванні задач на відсотковий склад речовин. Працювати над виробленням навичок розв’язувати за загальною схемою текстові задачі різного […]...

  40. Аналітичні способи розв’язування систем лінійних рівнянь із двома змінними Розв’яжіть задачі 1121. 1) х = 2y + 3; 2); х = -3у – 9; 3) х = 2у – 2,5; 4) х = 2y – 3. 1122. 1) у = 15 – 5х; 2) у = 4х + 6; 3) у = 6 – 2х; 4) у = 2 + 1,5х. 1123. 1) 2y […]...

Ви зараз читаєте: ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ
«
»