Ідеальний газ. Основне рівняння МКТ
ВЛАСТИВОСТІ ГАЗІВ, РІДИН, ТВЕРДИХ ТІЛ*
Урок № 5
Тема. Ідеальний газ. Основне рівняння МКТ
Мета: ознайомити учнів із рівнянням, що описує властивості речовин у газоподібному стані.
План уроку
1. Модель ідеального газу.
2. Тиск газу в МКТ.
3. Основне рівняння МКТ ідеального газу.
ХІД УРОКУ
I. Актуалізація опорних знань
1. Як сили взаємодії між молекулами залежать від відстані між ними?
2. Чому гази легко стискуються?
3. Чому стиснути тверді тіла, так само, як і рідини важко?
II. Вивчення нового матеріалу
1.
Ідеальний газ – це газ, у якому молекули можна вважати матеріальними точками, а силами притягання і відштовхування можна знехтувати.
У природі такого газу не існує, але близькими за властивостями можна вважати реальні розріджені гази, тиск у яких
2. Нехай газ міститься в закритій посудині. Манометр показує тиск газу р0. Але яка природа цього тиску? Кожна з молекул газу, ударяючись об стінку, протягом малого проміжку часу діє на неї з певною силою. Унаслідок безладних ударів об стінку, сила, що діє з боку всіх молекул на одиницю площі стінки,- це тиск. Дії, спричинені ударом окремих молекул, настільки малі, що манометр їх не реєструє. Манометр фіксує середню за часом силу, що діє на кожний квадратний сантиметр його чутливого елемента – мембрани. Середнє значення тиску р0 – практично цілком певна величина, бо ударів об стінку дуже багато, а маси молекул надзвичайно малі.
3. Нехай усередині посудини, площа стінки якої S, міститься ідеальний одноатомний газ, маса кожної молекули m0, вони хаотично рухаються зі швидкостями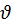 
.
Загальна кількість молекул у посудині N, а через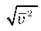 
позначимо середню квадратичну швидкість їх руху:
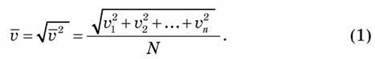
Експеримент свідчить, що у випадку незмінної температури посудини і газу, швидкість молекул газу також є сталою і визначається за формулою (1).
Квадрат вектора швидкості пов’язаний з його компонентами таким співвідношенням:
Повна хаотичність руху дозволяє стверджувати, що рух за всіма напрямами відбувається з однаковою швидкістю, тому
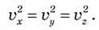
Тому формула 2 матиме вигляд:
Припустімо, що молекули газу рухаються від однієї грані до іншої без зіткнень.
Це спрощення внаслідок великої кількості молекул N і хаотичності їх руху не впливає на точність розрахунків. Під час зіткнення зі стінками посудини молекули ідеального газу взаємодіють з ними за законами механіки як абсолютно пружні тіла. Молекула діє на стінку із силою F2, що дорівнює, за третім законом Ньютона, силі F1, з якою стінка посудини діє на молекулу і протилежна їй за напрямом.
Нехай молекула масою т0 рухається в напрямку стінки посудини, площа якої S.
Пружно вдарившись об стінку, вона передає їй імпульс:
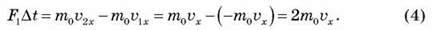
За час? t стінки посудини можуть досягти лише ті молекули, які містяться в об’ємі:
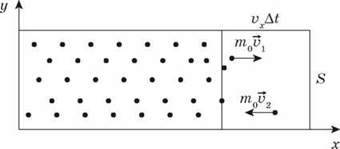
Оскільки в цьому об’ємі половина молекул рухається до стінки, а половина від неї, то кількість молекул Z, які вдаряться об стінку за час? t, дорівнюватиме:
Де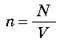 
– концентрація молекул, [n] = м-3. Підставивши значення об’єму V із рівняння (5) в рівняння (6) одержимо:
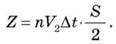
Усі ці молекули передають стінці посудини імпульс, що, згідно з другим законом Ньютона, дорівнює імпульсу сили:
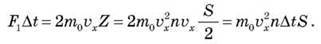
Після спрощення сила F, з якою діють молекули на стінку S, дорівнює:
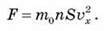
Оскільки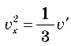 
, а тиск 
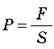, то одержимо вираз основного рівняння МКТ газів:
Врахуємо те, що квадрат модуля швидкості руху молекул дорівнює середньому значення квадрата швидкості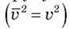 
, тож рівняння (7) матиме вигляд:
Це і є основне рівняння МКТ.
Тиск молекул на стінки посудини дорівнює 1/3 добутку концентрації молекул на масу однієї молекули і на середній квадрат швидкості руху молекул.
Основне рівняння МКТ пов’язує макроскопічні величини – тиск, який можна виміряти манометром, з мікроскопічними величинами, що характеризують молекули, і є ніби мостом між двома світами – макроскопічним та мікроскопічним.
Якщо через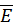 
0 позначимо середню кінетичну енергію поступального руху молекул
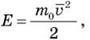
То рівняння (8) набуде такого вигляду:
Тиск молекул ідеального газу пропорційний добутку кількості молекул в одиниці об’єму на середню кінетичну енергію поступального руху молекул.
Оскільки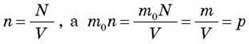 
, рівняння (8) набуде такого вигляду:
Де? – густина газу.
III. Закріплення вивченого матеріалу
Задача. Густина газу в балоні газопаливної електричної лампочки? = 0,9 кг/м3. Коли лампочка світиться, тиск газу зростає з р1 = 8-104 Па до р2 = 1,1-105 Па. На скільки збільшилась при цьому середня швидкість молекул газу?
Дано: р = 0,9 кг/м3, р1 = 8-104 Па, р2 = 1,1-105 Па.
Знайти: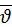 
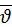2 – 1 – ?
Розв’язання
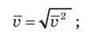
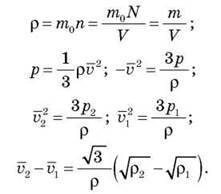
IV. Домашнє завдання
Вивчити конспект.
Задача. Під яким тиском перебуває газ у посудині, якщо середній квадрат швидкості його молекул 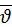2 = 106 м2/c2. Концентрація молекул n = 3-1025 м-3, маса кожної молекули m0 = 5-10-26 кг.
(1 votes, average: 5.00 out of 5)
Loading...