Коло, вписане в трикутник
Урок № 50
Тема. Коло, вписане в трикутник
Мета: домогтися засвоєння учнями змісту поняття кола, що вписане в трикутник, теореми про це коло, схеми її доведення та наслідку з неї.
Сформувати вміння:
– відтворювати формулювання означення і теореми про вписане в трикутник коло;
– за описом об’єктів розрізняти ті, в яких мова йде про коло, вписане в трикутник, та його елементи;
– виконувати побудову кола, вписаного в даний трикутник, та його елементів;
– розв’язувати задачі, спираючись на вивчений на уроці теоретичний
Тип уроку: засвоєння знань, умінь та навичок.
Наочність та обладнання: набір демонстраційного креслярського приладдя; таблиця “Коло, вписане в трикутник”.
ХІД УРОКУ
І. Організаційний момент
ІІ. Перевірка домашнього завдання
На цьому етапі слід звернути особливу увагу учнів на задачу № 1 (технологія побудови кола, описаного навколо трикутника) та опорну задачу. Для цього вчитель може або сам пояснити хід розв’язання задач, або викликати до дошки учнів з високим рівнем навчальних досягнень для презентації ними розв’язань цих задач.
Під час підготовки частини
Самостійна робота
1. Закінчіть речення: “Точка O – центр кола…” (див. рис.).
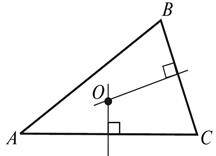
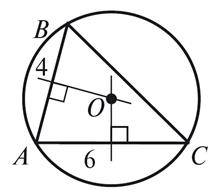
2. Дано: PABC = 30 (див. рис.). Знайдіть BC.
ІІІ. Мотивація навчальної діяльності. Формулювання мети й завдань уроку
Завдання. Який рисунок зайвий?
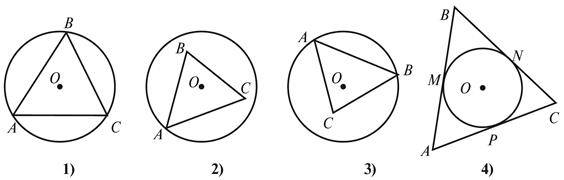
Чому? Опишіть це взаємне розташування кола і трикутника.
Виконавши пропоноване завдання, учні доходять висновку, що, окрім випадків взаємного розташування кола і трикутника, розглянутих на минулому уроці, потребує вивчення випадок, коли коло лежить у внутрішній області трикутника і сторони трикутника дотикаються до кола.
Учитель формулює основну мету уроку.
IV. Актуалізація опорних знань
Виконання усних вправ
1. На рисунку 1 CA – дотична до кола. Знайдіть кут BAO.
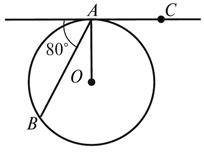
2. На рисунку 2 CA і CB – дотична до кола. Знайдіть:
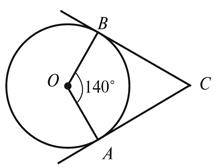
А) CB, якщо CA =10 см;
Б) кут C, якщо 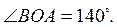
3. Що є ГМТ, рівновіддалених від:
А) двох точок;
Б) трьох точок, що не лежать на одній прямій;
В) сторін кута?
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Уявлення про коло, вписане в трикутник.
2°. Означення кола, вписаного в трикутник. Властивості центра та радіуса кола, вписаного в трикутник, та відрізків сторін, що виходить з однієї вершини.
3°. Теорема про вписане коло та її доведення.
4°. Наслідок з теореми про вписане коло.
Методичний коментар
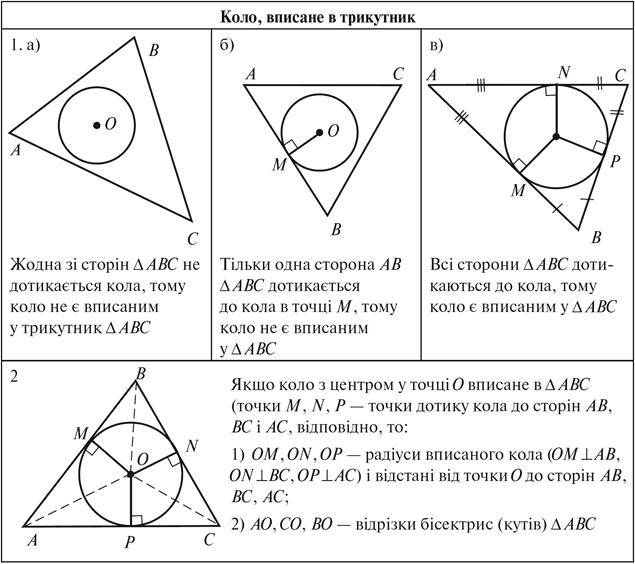
Так само як і під час вивчення кола, описаного навколо трикутника, розгляд питання уроку можна почати з контр прикладів 1а, 1б (див. таблицю), які демонструють, що не будь-яке коло, яке знаходиться у внутрішній області трикутника, буде називатися вписаним у цей трикутник колом.
Давши означення кола, вписаного в трикутник, слід звернути увагу учнів на властивості центра та радіуса вписаного кола, які широко застосовуються в задачах, а саме:
– центр вписаного в трикутник кола є точкою, рівновіддаленою від усіх сторін трикутника;
– радіус вписаного кола показує відстань (тобто довжину перпендикуляра) від центра кола до будь-якої сторони трикутника;
– виходячи із властивості відрізків, проведених до одного кола з даної точки, точки дотику вписаного в трикутник кола поділяють сторони трикутника на відрізки, з яких утворюються три пари рівних (рис. 3).
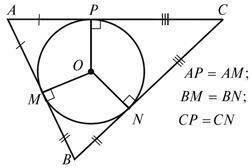
На закріплення зазначеної властивості можна запропонувати усно виконати завдання.
Завдання. На рисунку 3 AP = 5 см, CN = 2 см, BM = 3,5 см. Знайдіть периметр трикутника ABC.
Слід також звернути увагу на відомості про розташування центра вписаного кола відносно внутрішньої області трикутника.
VI. Первинне усвідомлення нового матеріалу
Виконання усних вправ
1. Дано трикутник і коло. Визначте, чи є дане коло описаним навколо трикутника або вписаним у нього, якщо:
А) центр кола рівновіддалений від усіх сторін трикутника;
Б) центр кола рівновіддалений від усіх вершин трикутника;
В) усі сторони трикутника – хорди кола;
Г) усі сторони трикутника дотикаються до кола.
2. Точка O – центр кола, вписаного в трикутник ABC. Чи означає це, що:
А) OA = OB;
Б) 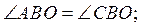
В) точка O може лежати поза даним трикутником?
3. Навколо трикутника описано коло, і в нього вписано коло. Чи можуть ці кола мати рівні радіуси; спільний центр?
Виконуючи усні вправи, звертаємося до таблиць “Коло, описане навколо трикутника”, “Коло, вписане в трикутник”.
Таблиця
Виконання письмових вправ
Рівень А
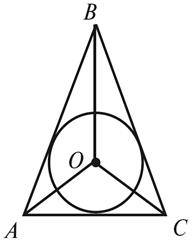
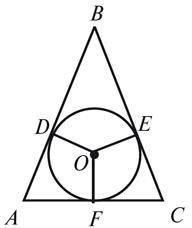
1. У рівнобедрений трикутник ABC (AB = BC) вписане коло з центром O (рис. 4).
А) Доведіть, що трикутник AOC рівнобедрений.
Б) Знайдіть кут ABC, якщо 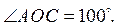
2. Побудуйте коло, вписане в даний трикутник.
3. Точка O – центр кола, вписаного в трикутник ABC. Знайдіть кут BAO, якщо 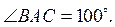
Рівень Б
У рівнобедреному трикутнику ABC з основою AC вписане коло дотикається до сторін трикутника в точках D, E і F (рис. 5). Знайдіть периметр трикутника, якщо AF = 5 см, BD = 6 см.
VII. Підсумки уроку
VIII. Домашнє завдання
Розв’язати задачі.
1. У трикутнику ABC бісектриси кутів A і C перетинаються в точці O. Знайдіть кут BAC, якщо 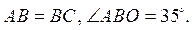
2. Точка дотику вписаного кола ділить бічну сторону рівнобедреного трикутника на відрізки 3 см і 5 см, починаючи від основи. Знайдіть периметр трикутника.
3 (опорна задача). У прямокутному трикутнику з катетами a, b і гіпотенузою c радіус вписаного кола обчислюється за формулою
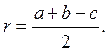
Доведіть.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.