Головна ⇒ 📌Довідник з геометрії ⇒ Конус

Конус

Геометрія

Тіла обертання

Конус

Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса.
Конус називається Прямим (далі просто “конус”), якщо пряма, що сполучає вершини конуса з центром основи, перпендикулярна до площини основи.
Прямий круговий конус можна розглядати як тіло, утворене

в результаті обертання ­прямокутного трикутника навколо його катета як осі.
Висота конуса – перпендикуляр, опущений із його вершини на площину основи.
Віссю прямого кругового конуса називається пряма, яка містить його висоту.
Зверніть увагу на рисунок нижче. Так звані “контурні твірні” SA i SB є дотичними до еліпса, який зображує основу конуса, точки A і B не є кінцями великої осі еліпса. Переріз конуса площиною, яка проходить через його вершину, – рівнобедрений трикутник, у якого бічні сторони є твірними конуса, а основою є хорда основи.
Конус
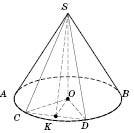
Розглянемо переріз CSD.
Він перетинає основу конуса по хорді CD.
Хорду CD видно з центра основи під кутом COD, а з вершини конуса – під кутом CSD.
Сам переріз – рівнобедрений 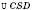Конус з основою CD, де 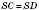Конус – твірні конуса. Його ортогональною проекцією на площину основи конуса є рівнобедрений 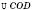Конус з основою CD і 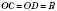Конус. Відрізок OK є бісектрисою, медіаною, висотою 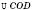Конус, відстанню від точки O до хорди CD. Відрізок SK є бісектрисою, медіаною, висотою 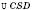Конус та відстанню від вершини конуса S до хорди CD. 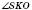Конус є лінійним кутом двогранного кута між площиною перерізу й площиною основи. Отже, 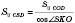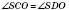Конус, Конус– кути нахилу твірної конуса до його основи.
Площа бічної поверхні конуса обчислюється за формулою 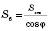Конус, де Sосн – площа основи, 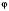Конус – кут нахилу твірної конуса до його основи.




Related posts:

  1. Зрізаний конус Геометрія Тіла обертання Зрізаний конус Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса. Така площина відтинає від конуса менший конус. Частина, що залишилась, називається Зрізаним конусом (див. рисунок): ; Зверніть увагу на осьовий переріз зрізаного конуса. Це рівнобічна трапеція, в якої основи – […]...
  2. Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
  3. Конус і зрізаний конус 983. Нехай дано конус, твірна якого AM = l, і нахилена до площини основи під кутом ∠MAO = α. А) ΔAMO – прямокутний. OM – висота, OM = l × sin α; Б) AO – радіус основи конуса. AO = l × cos α; В) ΔAMB – осьовий переріз; Г) площа основи конуса – площа […]...
  4. Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
  5. Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
  6. Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
  7. Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у па­ралельних […]...
  8. ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...
  9. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
  10. Куля Геометрія Тіла обертання Куля Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, […]...
  11. Конуси 1050. ΔSAPO: ∠АОР = 90°, ОЕ = АЕ = ЕР = 6,5 см → АР = 13 см. АО = 5 см. R = AO, L = АР = 13 см, r = 5 см. Sп. к. = πrl + πr2 = π(5 × 13 + 52) = 90π. S = 90π см2. 1051. ΟΑ […]...
  12. Куб, конус. Креслення розгорток куба, конуса УРОК 2 Тема. Куб, конус. Креслення розгорток куба, конуса Мета: навчити креслити розгортки куба, конуса; вдосконалювати уміння та навички роботи з папером; розвивати конструкторські уміння та навички; прищеплювати любов до праці; виховувати охайність, посидючість, працьовитість, правила естетики. Обладнання: папір, ножиці, клей, пензлик, олівець, гумка, серветка, таблиця для гри “Вгадайте слово”, циркуль. ХІД УРОКУ І. Організаційний […]...
  13. Зрізаний конус – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Зрізаний конус...
  14. Прямий круговий конус – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Прямий круговий конус...
  15. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...
  16. Кут між прямою та площиною Геометрія Стереометрія Кут між прямою та площиною Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину. Якщо пряма перпендикулярна до площини, то кут між нею й площиною вважається таким, що дорівнює , а між паралельними прямою та площиною таким, що дорівнює . Кут між прямою та площиною і […]...
  17. Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з да­ної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
  18. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...
  19. Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
  20. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...
  21. Геометричні побудови Урок № 52 Тема. Геометричні побудови Мета: продіагностувати рівень засвоєння учнями знань та вмінь, передбачений програмою під час вивчення теми “Геометричні побудови”. Тип уроку: перевірка і корекція знань, умінь та навичок. ХІД УРОКУ І. Організаційний момент ІІ. Перевірка домашнього завдання Зібрати зошити з домашньою контрольною роботою ІІІ. Умова контрольної роботи Варіант 1 Початковий рівень 1. […]...
  22. Існування площини, яка проходить через три дані точки УРОК 4 Тема. Існування площини, яка проходить через три дані точки Мета уроку: вивчення теореми про існування єдиної площини, яка проходить через три дані точки, які не лежать на одній прямій. Обладнання: стереометричний набір, моделі куба і тетраедра. Хід уроку 1. Один із учнів відтворює розв’язування задачі № 10, решта класу пише математичний диктант. 2. […]...
  23. Об’єм конуса і зрізаного конуса 1295. Нехай SA – твірна конуса, ∠SAO = α, SA = l. З ΔSAO : SO = SA × sin ∠SAO = I sin α, AO = AS × cos ∠SAO = І × cos α. Отже, об’єм конуса V дорівнює: Відповідь: 1296. Нехай радіус основи свинцевого конуса дорівнює r, а висота циліндра – H. […]...
  24. Побудова перерізів многогранників Урок 20 Тема. Побудова перерізів многогранників Мета уроку: формування вмінь учнів застосовувати властивості паралельних площин до розв’язування вправ, побудови перерізів. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Три учні відтворюють розв’язування задач № 28, 30, 31 на дошці, в цей час клас пише математичний диктант. 2. Математичний диктант. Через вершини А, В, […]...
  25. Кут між прямою і площиною Урок 54 Тема. Кут між прямою і площиною Мета уроку: формування поняття кута між прямою і площиною, а також умінь учнів знаходити кути між прямою і площиною. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Дайте означення кута між мимобіжними прямими. 2) Чи залежить кут між мимобіжними прямими від вибору прямих, які […]...
  26. Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...
  27. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
  28. Циліндр 940. Нехай дано циліндр, ABCD – осьовий переріз циліндра, AO = r – радіус циліндра, AC = d – діагональ осьового перерізу: А) ΔABC — прямокутний. BC – висота циліндра; Б) SABCD – площа діагонального перерізу. В) Площа бічної поверхні: Г) Площа поверхні циліндра 941. Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює D і […]...
  29. Многогранник Геометрія Многогранники Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників. Многогранник називається Опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Спільна частина такої площини й поверхні опуклого многокутника називається Гранню. На рисунку нижче зліва зображений не­опук­лий многогранник; на рисунку справа – опуклий. […]...
  30. Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
Ви зараз читаєте: Конус
«
»