КООРДИНАТНА ПЛОЩИНА. ГРАФІК ФУНКЦІЇ
РОЗДІЛ 4 ФУНКЦІЇ
&16. КООРДИНАТНА ПЛОЩИНА. ГРАФІК ФУНКЦІЇ
Із кypcу математики 5-6 класів ви знаєте, що таке шкала, координатна пряма і координатна площина. Пригадаємо основні відомості.
Щоб увести прямокутну систему координат на площині, треба: провести дві координатні прямі з рівними одиничними відрізками так, щоб вони перетиналися під прямим кутом у початку їх відліку (початку координат); стрілками вказати додатний напрямок на кожній з осей; визначити, яку з осей вважати першою координатною віссю (віссю абсцис), а яку – другою
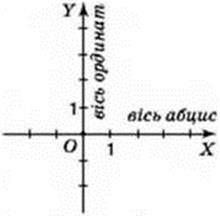
Мал. 9
Площина з уведеною на ній системою координат називається координатною площиною.
Координатні осі позначають так: ОХ (вісь абсцис) і OY (вісь ординат).
Кожній точці на площині можна поставити у відповідність пару чисел, взятих у певному порядку, і навпаки, кожній парі чисел відповідає єдина точка координатної площини. Така упорядкована пара чисел називається координатами точки в даній системі координат. На малюнку 10 точка А має координати: х = 3,у = 2.
Коротко записують: А (3; 2). Читають: “Точка А з координатами 3 і 2”.
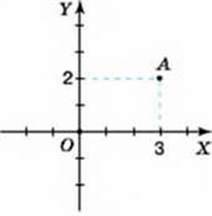
Maл.
Зверніть увагу:
Щоб визначити координати точки в даній системі координат:
1) через дану точку проведіть прямі, паралельні осям координат;
2) на координатних осях відмітьте числа, які відповідають точкам перетину цих прямих з осями;
3) з отриманих чисел утворіть упорядковану пару – координати точки.
Якщо точка лежить на осі абсцис, то ЇЇ ордината дорівнює 0. Якщо точка лежить па осі ординат, то її абсциса дорівнює 0. І навпаки, якщо абсциса (ордината) точки дорівнює нулю, то точка лежить на осі ординат (абсцис). Початок координат О має координати (0; 0).
Задача 1. На координатній площині побудуйте точку В (-3;2).
Розв’язання. Уведемо систему координат на площині (мал. 11). На осі абсцис відмітимо число -3, що є першою координатою даної точки, а на осі ординат – число 2, яке є другою її координатою. Через ці точки на осях координат проведемо дві прямі, паралельні осям (мал. 11).
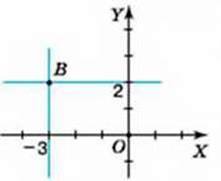
Мал. 11
Точка перетину побудованих прямих – шукана точка В (-3; 2).
Координатні осі розбивають координатну площину на чотири частини. їх називають координатними чвертями і позначають так: І чверть, II чверть, ІІІ чверть, IV чверть (мал. 12).
Подивіться на малюнки 13 і 14. Ви бачите ту саму лінію, яку зображено як геометричну фігуру на площині (мал. 13) і як грaфік на координатній площині (мал. 14). За першим малюнком можна з’ясувати геометричні властивості даної лінії – яка її форма, розміри, взаємне розміщення її частин тощо. За другим малюнком можна з’ясувати не лише геометричні, а й алгебраїчні властивості цієї лінії. Наприклад, її точкам властиве таке:
1) абсциси змінюються від -4 до 4, а ординати від -16 до 16;
2) кожній абсцисі відповідає єдина ордината;
3) якщо х = 0, то у = 0;
4) якщо значення х додатне (від’ємне), то і значення у додатне (від’ємне);
5) зі збільшенням абсциси ордината збільшується, а зі зменшенням – зменшується;
6) абсциси й ординати точок пов’язані певною залежністю. Якщо цю залежність подати формулою, то дістанемо: у = 0,25х3, де -4 ≤ х ≤ 4.
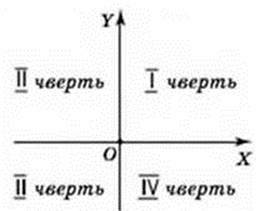
Мал. 12
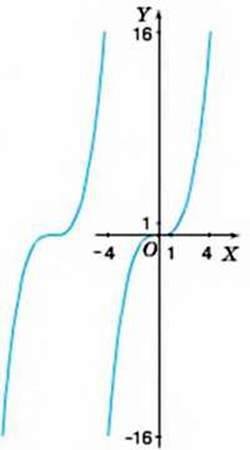
Мaл. 13 Мал. 14
? Чи є отримана залежність функцією? Так, оскільки залежність у = 0,25 х3 задовольняє означення функції, причому для будь-яких чисел.
Виходить, що па малюнку 14 зображено лише частину графіка функції у = 0,25х3 (тільки для -4 < х < 4). Якщо надавати х інших значень із області визначення даної функції, зокрема менших від -4 або більших за 4, то зображену лінію можна продовжити, причому нескінченно.
Запам’ятайте!
Графіком функції у = f(x) називається зображення на координатній площині всіх точок, абсциси яких є значеннями аргументу, а ординати – відповідними значеннями даної функції.
? На малюнку зображають лише частину графіка функції, а говорять: “Графік функції”.
Задача 2. Побудуйте графік функції у = х2 – 1.
Розв’язання. Область визначення даної функції – будь-які числа. Складемо таблицю її значень для -2 ≤ х ≤ 2 із кроком 0,5 (табл. 18).
Таблиця 18
Х | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
У(х) | 3 | 1,25 | 0 | -0,75 | -1 | -0,75 | 0 | 1,25 | 3 |
Пари значень х і у у таблиці 18 є координатами точок шуканого графіка. На координатній площині побудуємо ці точки (мал. 15).
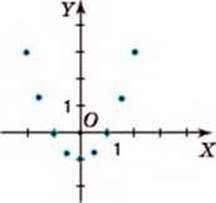
Мал. 15
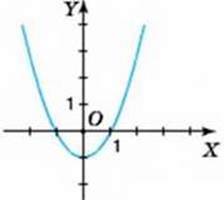
Мал. 16
Оскільки область визначення даної функції – усі числа, то її графіку належать й інші точки. Щоб їх побудувати, треба взяти менший крок для абсцис. Якщо крок буде досить маленьким, то отримаємо майже суцільну лінію. Це простіше зробити, скориставшись комп’ютером. Ми ж будемо вважати, що побудовані точки можна з’єднати плавною лінією (мал. 16). Отриманий графік – шуканий.
Зверніть увагу:
Щоб побудувати графік функції:
1) знайдіть її область визначення;
2) складіть таблицю значень функції для кількох значень аргументу;
3) на координатній площині побудуйте точки за їх координатами з таблиці;
4) з’єднайте ці точки плавною лінією, якщо це допускає область визначення функції.
? Чи може графік функції складатися лише з окремих точок? Так. Наприклад, графік функції у = 3n + 2, де n – натуральні непарні одноцифрові числа, містить лише 5 точок (мал. 17).
Задача 3. Чи належить графіку функції у = – х + 2 точка:
1)А (-3; 5); 2) Б (1; 3)?
Розв’язання. 1. Підставимо координати точки А у формулу, що задає функцію, та виконаємо обчислення: 5 = -(-3) + 2, або 5 = 5. Дістали правильну числову рівність, тому точка А належить графіку даної функції.
2. Підставимо координати точки В у формулу, що задає функцію, та виконаємо обчислення: 1 ≠ -3 + 2, або 1 ≠ -1. Дістали неправильну числову рівність, тому точка В не належить графіку даної функції.
Мал. 17
Зверніть увагу:
– якщо координати точки задовольняють формулу, якою задано функцію, то ця точка належить графіку функції.
– якщо точка належить графіку функції, то її координати задовольняють формулу, якою задано функцію.
? Чи будь-яка лінія, яку побудовано в прямокутній системі координат XOY, задає функцію? Ні. Наприклад, коло на малюнку 18 не може задавати функцію, оскільки існують такі значення незалежної змінної х (зокрема -2 < х < 2), яким на даному зображенні відповідає більше ніж одне значення залежної змінної у.
Загалом уважають, що функцію задано графічно у прямокутній системі координат, якщо в цій системі зображення містить принаймні одну точку і на ньому немає двох точок
З рівними абсцисами, але різними ординатами. Звідси випливає, що будь-яка пряма, перпендикулярна до осі ОХ, перетинає графік функції не більше, ніж в одній точці.
Подивіться на малюнок 19. Ви бачите графік функції у = -0,25х3. Порівняємо його з графіком функції у = 0,25х3 (див. мал. 14). Для функції у = 0,25×3 характерна така властивість: що більшими є абсциси точок, то більшими є їх ординати. Таку функцію називають зростаючою. У функції у = -0,25×3 властивість інша: що більшими є абсциси точок, то меншими є їх ординати. Таку функцію наливають спадною.
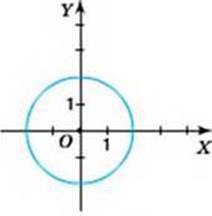
Мал. 18
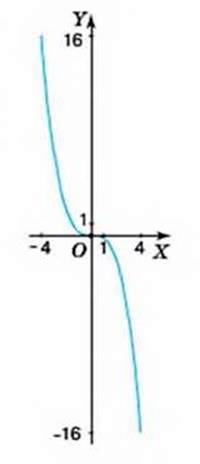
Мал. 19
Дізнайтеся більше
1. Рене Декарт (1596 – 1650) – французький філософ, фізик, математик, засновник аналітичної геометрії – розділу геометрії, в якому геометричні фігури та їх властивості досліджуються засобами алгебри. У математиціДекарт, крім декартової системи координат, дав поняття змінної величини і функції, увів багато алгебраїчних означень. У фізиці він сформулював закон збереження кількості руху, запровадив поняття імпульсу сили. У психології вчений відкрив поняття про рефлекс і принцип рефлекторної діяльності.
2. Уперше прямокутну систему координат увів Рене Декарт у своїй роботі “Міркування про метод”, яка побачила світ у 1637 р. Тому прямокутну систему координат називають також прямокутною декартовою системою координат. Координатний метод опису геометричних об’єктів поклав початок аналітичній геометрії. Значний вклад у розвиток координатного методу також вніс П’єр Ферма (1601 – 1665).
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Поясніть, як побудувати прямокутну систему координат на площині.
2. Яку назву мають осі координат? Точка їх перетину?
3. Що називають координатною площиною?
4. Поясніть, як визначити координати точки.
5. Які координати має початок координат?
6. Які координати має точка, що лежить на осі абсцис; на осі ординат?
7. На скільки координатних чвертей розбивають площину координатні осі?
8. Що називається графіком функції?
9. Чи будь-яка геометрична фігура може бути графіком функції?
10. Як побудувати графік функції?
11. Як визначити, чи належить точка графіку функції?
12. Поясніть, яка функція називається зростаючою; спадною.
РОЗВЯЖІТЬ ЗАДАЧІ
824. Дано точку А(-3; 7). Чи правильно, що:
1) абсциса точки A дорівнює: а)-3; б)3; в)-7; г)7;
2) ордината точки A дорівнює: а) -3; б) 3; в)-7; г)7?
825. Не виконуючи побудови, з’ясуйте, у якій координатній чверті міститься точка:
А(-1.5; 2,3), В(5,19; -4,72), С (1 
;), D (5 
;4,77), E (6 
;108), F(-102; -203), K(-3,345; 1,032), L (-45 
;47,85).
826 . Чи може бути графіком деякої функції лінія, зображена:
1) на малюнку 20; 2) на малюнку 21; 3) на малюнку 22?
Мал. 20
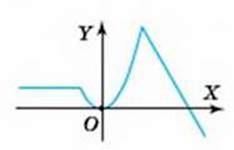
Мал. 21
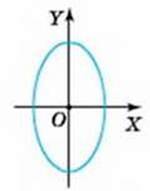
Мал. 22
827. Чи правильно, що точка О (0; 0) належить графіку функції:
1) y = 3х – 3; 2)у = х2 + 1; 3)y = – x2
828. Чи правильно, що графік функції у = х2 проходить через точку:
1)А(1; 1); 2)5 (-2; -4); 3)С(0; 0)?
829. Які з даних точок А(-4,5; 0), Б(8,03; 1,05), С(0,6; 3,1), D(0; -1,77), Е (5 
;0), F(0,3; 0), К (0; -1 
;0), L(0,33; 0,66), М(0; 0) лежать на осі: 1) абсцис; 2) ординат?
830. Накресліть систему координат. На осі ОХ позначте точку з абсцисою: 1) 2,5; 2)-3,5; 3) 5; 4)-1,5. Запишіть координати цих точок.
831. Накресліть систему координат На осі OY позначте точку з ординатою: 1)3; 2) -0,5; 3) 3,5; 4) -4. Запишіть координати цих точок.
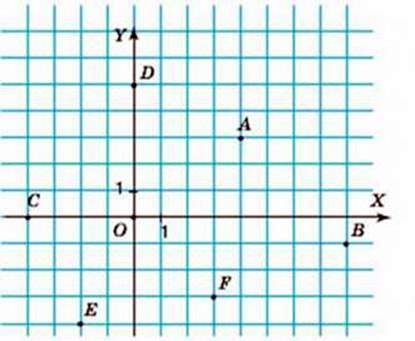
Мал. 23
Мал. 24
832. Визначте координати точок, зображених на малюнку 23.
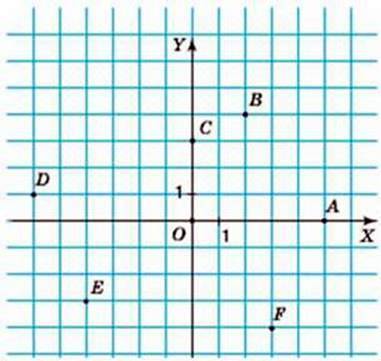
833. Визначте координати точок, зображених на малюнку 24.
834. Задайте прямокутну систему координат на площині та позначте на ній точки: А (2; 1), В (2; -1), С (-1,5; 3,5), D (3; -2,5), Е (3; 3), F (4; 3), G (-3; -4), Н (-4; -3). Побудуйте прямі АС, DG. EH, BF.
835. Задайте прямокутну систему координат на площині та позначте на ній точки: K(-1,4; -1,2), L(-1,4; 0,6), М(-1,6; -0,8), N(0,6; -1). Побудуйте прямі КМ, LM, LN.
Мал. 25
Мал. 26
Мал. 27
Мал. 28
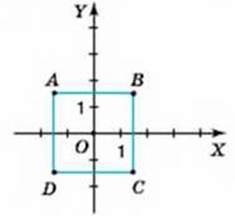
836. Визначте координати вершин квадрата, зображеного:
1) на малюнку 25; 2) на малюнку 26.
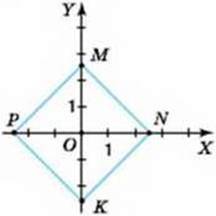
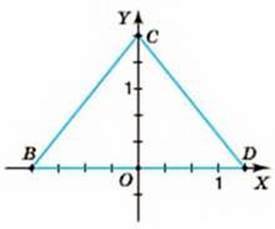
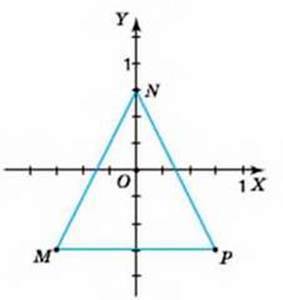
837. Визначте координати вершин трикутника, зображеного:
1) на малюнку 27; 2) на малюнку 28.
838 На малюнку 29 зображено графік деякої функції. Користуючись графіком, знайдіть:
1) область визначення функції;
2) область значень функції;
3) значення у, якщо х = -2; 0; 1; 3,5;
4) значення х, за яких у = 0;
5) три значення аргументу, за яких значення функції додатне;
6) три значення аргументу, за яких значення функції від’ємне;
7) значення аргументу, за яких функція зростає;
8) значення аргументу, за яких функція спадає.
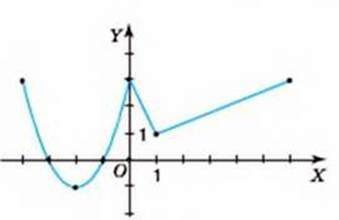
Мал. 29
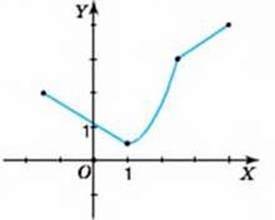
Maл. 30
839. На малюнку 30 зображено графік деякої функції. Користуючись графіком, знайдіть:
1) область визначення функції;
2) область значень функції;
3) значення у, якщо х = -1,5; 1; 2,5; 4;
4) значення х, за яких у = 0;
5) три значення аргументу, за яких значення функції додатне;
6) три значення аргументу, за яких значення функції від’ємне;
7) значення аргументу, за яких функція зростає;
8) значення аргументу, за яких функція спадає.
840. Функцію задано формулою: у = – х2 + 2. Перемалюйте в зошит і заповніть таблицю 19.
Таблиця 19
X | -2 | -1 | 0 | 1 | 2 |
Y |
Користуючись даними таблиці, побудуйте графік функції.
841. Функцію задано формулою: у = 2х2 – 1. Перемалюйте в зошит і заповніть таблицю 20.
Таблиця 20
X | -2 | -1 | 0 | 1 | 2 |
Y |
Користуючись даними таблиці, побудуйте графік функції.
842. Складіть таблицю значень функції, заданої формулою у = х(3х – 1), де -2 ≤ х ≤ 2, з кроком 0,5. Користуючись даними таблиці, побудуйте графік даної функції.
843. Чи належить графіку функції у = – х2 – З точка:
1)A(-1;-4); 2)B (1; 4); 3)С(0; 3); 4)D(-2;-5)?
844. Яка з точок М (-1; -2), N (1; -2), Р (2; -7), R (-2; 7) належить графіку функції у = – х3 – 1 ?
845. Назвіть будь-які чотири точки, які належать графіку функції:
1) у = -2х2 + 1; 2) у = 0,5х3 – 1.
846. Чи належить графіку функції у = 4 – х2 точка:
1)K(-1; 3); 2) L (1; -3); 3)M(2; 0); 4) N(-2; 6)?
847. Чи проходить через початок координат графік функції:
1) y = 5х2; 2) у = -3х2 + 4; 3) у = 
Х?
848. Чи перетинає вісь абсцис графік функції:
1) у = 2х2 + 3; 2) у = -3х2 – 4; 3) y =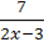 
?
849. У якій точці перетинає вісь ординат графік функції:
1)у = 4х – 4; 2) у = -3х2 + 3; 3) y = – 
X + 
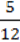Y?
850. У якій точці перетинає вісь абсцис графік функції:
1) y = 5х – 15; 2)у = – х2 + 9; 3) y = –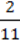 
X +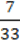 
?
851. Графік функції у = х2 + n проходить через точку N (-2; 6). Знайдіть значення n.
852. Графік функції у = k – 2х2 проходить через точку К (1; 2). Знайдіть значення k.
853. Графік функції у = х2 – m проходить через точку М (-1; -4). Знайдіть значення m.
854. Графік функції у = ах – 1 проходить через точку A (-1; -1). Знайдіть значення а.
855. Графік функції у = 4 – сх проходить через точку C (2; 2
). Знайдіть значення с.
856. Графік функції у = bх – 1 проходить через точку B (2; 
). Знайдіть значення b.
857. Запишіть координати точки М, якщо з точкою N(-5,5; 4,2) вона має:
1) рівні абсциси, але протилежні ординати;
2) рівні ординати, але протилежні абсциси;
3) протилежні абсциси і протилежні ординати;
4) рівні абсциси і рівні ординати.
858. Дано точку D(4,8; -1,5). Запишіть координати точки С, якщо її абсциса й ордината:
1) протилежні до відповідних координат точки D;
2) утричі менші від абсциси й ординати точки D відповідно;
3) на 1,3 більші за абсцису й ординату точки D відповідно.
859. Дано точку K (-3; 2
). Запишіть координати точки L, якщо її абсциса й ордината:
1) відповідно дорівнюють півсумі та піврізниці абсциси й ординати точки К;
2) у 5 разів менші від абсциси й ординати точки К відповідно;
3) на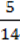 
більші за абсцису й ординату точки К відповідно.
860. Побудуйте пряму MN, якщо М(1; 1), N(-3; -3). Визначте координати ще чотирьох точок цієї прямої. Яку закономірність ви помітили?
861. Побудуйте пряму PQ, якщо Р(-3,5; 3,5), Q(2; -2). Визначте координати ще чотирьох точок цієї прямої. Яку закономірність ви помітили?
862. Кожному натуральному числу поставили у відповідність суму його потроєного квадрата та числа, протилежного до числа 3. Задайте цю функцію формулою та побудуйте її графік.
863. Побудуйте графік функції у = (х – 2)2 – 1, якщо -1 ≤ х ≤ 4.
Користуючись графіком, знайдіть:
1) значення у, якщо х = 0; 1,5; 2,5;
2) значення х, за яких у = -0,75; 0; 3;
3) значення аргументу, за яких значення функції додатне;
4) значення аргументу, за яких значення функції від’ємне;
5) значення аргументу, за яких функція зростає;
6) значення аргументу, за яких функція спадає.
864. Побудуйте графік функції у = (х + 1 )2 + 1, якщо -3 < х < 1. Користуючись графіком, знайдіть:
1) значення у, якщо х = -2,5; -1; 0;
2) значення х, за яких у = 1; 2; 3,25;
3) значення аргументу, за яких значення функції додатне;
4) значення аргументу, за яких значення функції від’ємне;
5) значення аргументу, за яких функція зростає;
6) значення аргументу, за яких функція спадає.
865. Побудуйте графік функції:
1) y = 0,5х2 – 1,5, якщо -3 < х < 3;
2) y =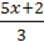 
, якщо -2 ≤ х ≤1;
3) y = X2 –, якщо -2 ≤ х ≤ 2;
4) y =0,2×2 – 1,2, якщо -4 ≤ х ≤ 4;
5) y = 
+ 1, якщо -7 ≤ х ≤ 7;
6) y = 
X2 + 
, якщо -3 ≤ х ≤ 3;
866. Побудуйте графік функції:
1) y = – 1,5х2 + 3, якщо -2 < х < 1;
2) y =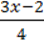 
, якщо -2 ≤ х ≤3;
3) y = 
X2 – 
, якщо -1 ≤ х ≤ 2;
867. В одній системі координат побудуйте графіки функцій у = х2 та у = – х. Знайдіть координати точок перетину цих графіків. Укажіть, за яких значень аргументу графік функції у = х2 лежить вище, ніж графік функції у =-х.
868. В одній системі координат побудуйте графіки функцій у = – х3 та у = х. Знайдіть координати точок перетину цих графіків. Укажіть, за яких значень аргументу графік функції у = – х3 лежить нижче, ніж графік функції у= х.
869. Побудуйте множину точок М(х; у), якщо:
1) -3 < х< 1, у =2; 3)-3,5 < х < 0,5, у = 2,5;
2) -2 < у< 2, х=1; 4) -6 < y <3, х = .
870. Побудуйте множину точок Q(x; у), якщо:
1) -2 < х < 1,5, -2 < у < 1,5; 3) -0,5 < х < 0,5, -3 < у < 3;
2) -4 < у <-2, -3 < х < -1; 4) -2,5 < у <-0,5, -3,5 < х < 0.
871. Побудуйте всі точки Р(х; у) такі, що | х | < 2, | у | < 5 і:
1) ордината точки Р протилежна до її абсциси;
2) модуль ординати точки Р дорівнює її абсцисі;
3) абсциса точки Р удвічі менша від її ординати.
872. Побудуйте графіки функцій у = | х | та у = – х2 + 2. Знайдіть координати точок перетину цих графіків.
873. Побудуйте графіки функції:
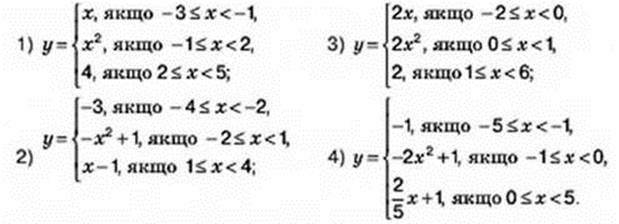
874. Побудуйте графік функції, якщо її область визначення – множина всіх чисел, а кожне значення функції дорівнює найбільшому цілому числу, що не перевищує відповідного значення аргументу.
875. Побудуйте графік функції, якщо її область визначення – множина всіх чисел, а кожне значення функції дорівнює різниці між значенням аргументу та найбільшим цілим числом, що не перевищує відповідного значення аргументу.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
876. У понеділок до магазину завезли 5 ящиків цукерок “Ромашка” по 10 кг у кожному. Щодня магазин продає 6,5 кг цукерок. Запишіть у вигляді формули залежність маси цукерок, що залишились в магазині, від дня тижня. Визначте, скільки цукерок залишиться у магазині в середу, п’ятницю та неділю. Побудуйте графік отриманої функції.
877. Побудуйте графік зміни температури за будь-який день тижня, знімаючи покази через кожні 2 години. З’ясуйте:
1) у який час дня температура була найвищою;
2) у який час дня температура була найнижчою;
3) коли в цей день температура знижувалась;
4) коли в цей день температура підвищувалась.
ЗАДАЧІ НА ПОВТОРЕННЯ
878. Обчисліть, не використовуючи калькулятор:
1) 262 – 162; 2) 1172 – 172; 3) 2062; 4) 1982.
879. Одна сторона трикутника дорівнює 2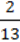 
м, друга – у 
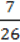раза менша від першої, а третя – у 
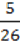раза більша за другу.
Знайдіть периметр трикутника.
880. Знайдіть найбільший спільний дільник чисел:
1)225 і 400 ; 2) 144 і 360; 3)630 і 780.
881. Андрій поклав у банк 3000 гривень на два роки під 15 % річних. Скільки грошей отримає Андрій через два роки?
(1 votes, average: 5.00 out of 5)
Loading...