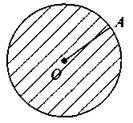
Круг. Площа круга
Урок № 5 7
Тема. Круг. Площа круга
Мета: сформувати уявлення учнів про геометричну фігуру круг та поняття площі круга; навчити користуватися формулою S = nR2 для розв’язування задач.
Тип уроку: засвоєння знань, умінь та навичок.
Хід уроку
I. Перевірка домашнього завдання
Математичний диктант
Варіант 1 [2]
1. Запишіть формулу, за якою обчислюється довжина кола, якщо відомий його радіус [діаметр].
2. Обчисліть довжину кола, якщо довжина діаметра [радіуса] його 10 м [5 дм], число? округліть до сотих.
3. Довжина кола 9,42 дм.
4. Діаметр кола більший за радіус кола на 7 см. [Радіус кола менший від його діаметра на 14 дм]. Яка довжина кола? Число? виразіть звичай ним неправильним дробом.
II. Актуалізація опорних знань
1. Під час перевірки результатів виконання диктанту повторюємо основний зміст матеріалу попереднього уроку (уявлення про коло, радіус, діаметр кола; довжина кола і число я у вигляді десяткового та звичайного дробу).
2. Окрім цього, слід ще повторити деякі поняття. Для цього виконуємо усні вправи:
1) Назвіть геометричні фігури, які ви бачите на рисунку:
Яка з них зайва?
2) Якою величиною характеризується будь-який відрізок? Які одиниці вимірювання довжини ви знаєте?
3) Якою величиною характеризується частина площини, що обмежена сторонами квадрата? прямокутника? Які одинці вимірювання площі ви знаєте?
4) Обчисліть площу і периметр:
А) квадрата зі стороною 7 см;
Б) прямокутника зі сторонами 7,5 см і 6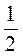
См.
III. Засвоєння знань
@ Як і на попередньому уроці, розпочати треба з того, що повторити зміст поняття “круг” і показати різницю між цим поняттям і поняттям “кола”, тільки після цього знайомимо учнів з формулою площі кола і показуємо її застосування для розв’язування задач.
1. Круг. Елементи круга
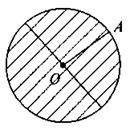
Накреслимо коло с центром в т. О і радіусом ОА = R = 3 см. Це коло поділить площину (аркуш) на 2 частини, одна з яких лежить зовні, а інша – всередині кола.
Тоді частина площини, що знаходиться всередині кола разом із колом – круг, О – центр і R = OA – радіус.
2. Площа круга.
@ Досвід автора показує, що виведення формули площі круга через площу вписаного і описаного квадратів шестикласникам не дуже зрозуміло. Тому, на розсуд учителя, або “виводимо” формулу, як це робиться традиційно в підручниках з математики для 6 класу, або пояснюємо, що ця формула буде виведена нами у 9 класі, коли ми навчимося це робити, спираючись на відповідні геометричні відомості, і записуємо формулу S = nR2. Наприкінці пояснень, маємо записати в зошитах учнів (конспект 27).
Конспект 27 | ||
Круг. Площа круга | ||
Круг з центром О, Радіус ОА = R; S = nR2 – площа круга |
| Приклади 1) Якщо R = 2 см, То S = nR2 = n-22 = 4n (см2). 2) Якщо D = 2 см, То R = D : 2 = 2 : 2 = 1см. S = nR2 = n (см2) |
IV. Засвоєння вмінь
Усні вправи
1. Обчисліть: 12; 32; 0,12;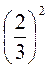 
; 1,12.
2. Знайдіть площу круга радіуса 1 м; 10 дм.
3. Від геометричної фігури площею 10 дм2 відрізали частину площею 2 дм2; 15 см2. Яка площа тієї частини, що залишилась?
Письмові вправи
1. Знайдіть площу круга: а) радіуса 5 см; 11 см; 0,2 м; б) діаметра 0,5 м; 8 м.
2. Довжина кола арени цирку дорівнює 47,1 м. Знайдіть площу арени (результат округліть до м2).
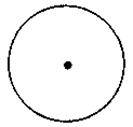
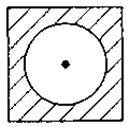
3. Зробіть необхідні вимірювання та знайдіть площі заштрихованих фігур, зображених на рисунку.
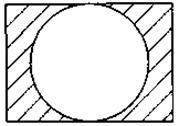
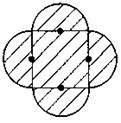
Перед виконанням задачі 3 бажано розглянути додаткові задачі.
Додаткові задачі
Задача 1. Знайдіть площу заштрихованих фігур 1-3, якщо площа даної фігури S (од. кв.)
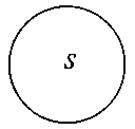
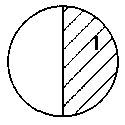
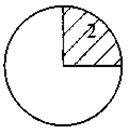
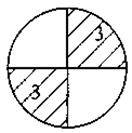
Задача 2. Як Знайдіть площу заштрихованих фігур 4-6 :
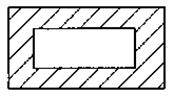
4)
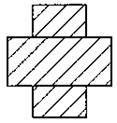
5)
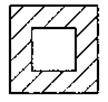
6)
V. Підсумки уроку
VI. Домашнє завдання
Задача 1. Знайдіть площу круга:
А) радіуса 8 см; 14 дм; 3,5 м; б) діаметра 1,6 м; 5 дм.
Задача 2. Знайдіть площу круга, якщо довжина його кола дорівнює 25,12 см.
Задача 3. Треба пофарбувати круг радіуса 3 м. Скільки потрібно для, цього фарби, якщо на кожний квадратний метр витрачається 120 г фарби (результат округліть до десятків грамів)?
Задача 4. Клумба має форму круга. Довжина кола, що обмежує клумбу, дорівнює 31,4 м. На клумбі висаджують кущі троянд, відводячи під кожний кущ 0,8 м2 землі. Яку найбільшу кількість кущів троянд можна висадити на клумбі?
(1 votes, average: 5.00 out of 5)
Loading...