Квадратична функція – Функції та графіки
Математика – Алгебра
Функції та графіки
Квадратична функція
Квадратним тричленом називається многочлен виду 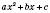 , де x – змінна, a, b і c – деякі числа, причому
, де x – змінна, a, b і c – деякі числа, причому 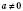 .
.
Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння 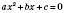 .
.
Теорема. Якщо 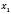 і
і 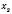 – корені квадратного
– корені квадратного
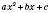 , то
, то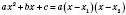 .
.Приклади
1)
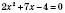 ,
,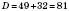 ,
,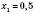 ;
; 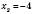 .
.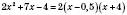 або
або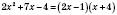 .
.2) Скоротити дріб.
а)
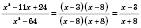 ;
;б)
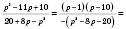
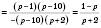 ;
;в)
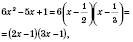
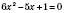 ,
, 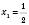 ;
; 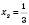 .
.Квадратичною функцією називається функція, яку можна задати формулою виду
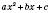 , де x – незалежна змінна, a, b, c – довільні числа, причому
, де x – незалежна змінна, a, b, c – довільні числа, причому 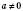 .
.Графіки функцій
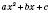 і
і 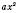 – рівні параболи, які можна сумістити паралельним перенесенням.
– рівні параболи, які можна сумістити паралельним перенесенням.Будь-яку функцію
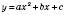 можна представити у вигляді
можна представити у вигляді 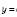 , де m і
, де m і 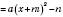 , n – деякі дійсні числа. А це означає, що графік функції
, n – деякі дійсні числа. А це означає, що графік функції 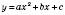 можна дістати за допомогою двох паралельних перенесень графіка функції
можна дістати за допомогою двох паралельних перенесень графіка функції 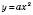 .
.Приклад
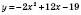 ;
;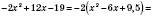
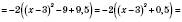
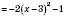 .
.Отже, щоб дістати графік функції
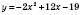 , треба зробити з графіком функції
, треба зробити з графіком функції 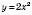 такі перетворення:
такі перетворення:1) відобразити симетрично осі Ox;
2) зробити паралельне перенесення на три одиничних відрізка в напрямі осі Ox;
3) зробити паралельне перенесення на один одиничний відрізок униз.
Зробимо всі ці перетворення й отримаємо графік функції
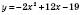 :
: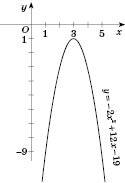
При побудові параболи користуються такими загальними формулами та властивостями квадратичної функції.
1. Координати вершини параболи
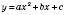 :
:xв=
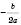 ; yв=
; yв= 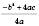 або yв= y(xв).
або yв= y(xв).Зручніше знаходити ординату вершини як значення функції, що відповідає значенню аргументу x = xв.
2. Точки перетину параболи з осями координат є такими:
Абсциса точки перетину параболи з віссю Oy дорівнює 0, тоді
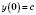 ,
, 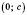 .
.Ордината точок перетину параболи з віссю Ox дорівнює 0, тоді, щоб знайти абсциси цих точок, треба розв’язати квадратне рівняння
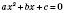 .
.Якщо це рівняння має два різних корені
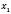 і
і 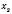 , графік перетинає вісь Ox у точках
, графік перетинає вісь Ox у точках 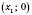 ,
, 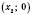 .
.Якщо це рівняння має один корінь (тобто
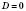 ), то цей корінь
), то цей корінь 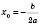 .
.Це означає, що вершина параболи лежить на осі Ox і має координати
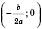 .
.Якщо це рівняння не має коренів
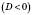 , парабола не перетинає вісь Ox.
, парабола не перетинає вісь Ox.3. Напрям віток параболи залежить від знака коефіцієнта a.
Якщо
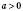 , вітки параболи напрямлені вгору.
, вітки параболи напрямлені вгору.Якщо
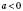 , вітки параболи напрямлені вниз.
, вітки параболи напрямлені вниз.4. Парабола є симетричною відносно прямої
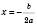 .
.На рисунках, поданих нижче, наведені ескізи розміщення параболи на координатній площині в деяких випадках.
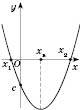
1)
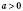 ;
; 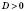 ;
;
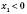 ;
; 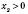 ;
;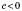 ; xв
; xв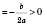 .
.2)
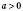 ;
; 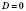 ;
;x1 = x2 = xв=
=
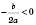 ;
;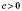 .
.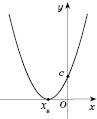
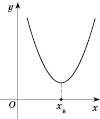
3)
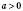 ;
; 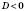 ;
;xв> 0;
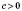 .
.
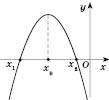
4)
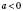 ;
; 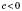 ;
;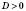 ;
;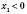 ,
, 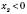 ;
;xв=
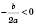 .
.
5)
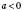 ;
; 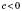 ;
;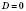 ;
;x1= x2= xв=
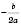 <0.
<0.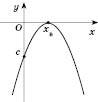
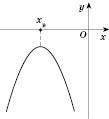
6)
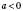 ;
; 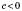 ;
;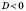 ;
;xв=
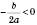 .
.
Приклад
Побудувати графік функції
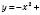
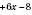 .
. 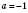 – вітки параболи напрямлені вниз.
– вітки параболи напрямлені вниз.xв=
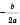 ; xв=
; xв= 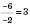 ;
;yв=
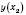 , yв=
, yв= 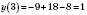 .
.Вершина: (3; 1).
Точка перетину з віссю Oу:
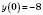 ; (0; –8).
; (0; –8).Точки перетину з віссю Ox:
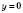 ;
; 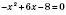 ;
;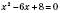 ;
; 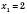 ,
, 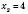 .
.(2; 0); (4; 0).
На прикладі цієї функції покажемо, як аналізувати її властивості.
1.
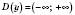 .
.2.
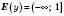 ;
; 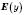 – множина значень функції, тобто множина всіх значень y.
– множина значень функції, тобто множина всіх значень y.3.
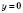 при
при 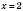 і при
і при 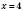 .
.4. Точки перетину графіка з осями координат.
(0; -8); (2; 0); (4; 0).
5.
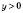 при
при 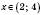 ;
; 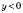 при
при 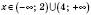 .
.6. Функція зростає при
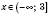 , функція спадає при
, функція спадає при 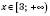 .
.7. Найбільше значення функції –
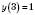 , найменшого значення функції немає.
, найменшого значення функції немає.8. Графік функції – парабола (див. рисунок нижче), що дорівнює параболі
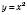 , вітки якої напрямлені вниз, яка має вершину в точці (3; 1) і симетрична відносно прямої
, вітки якої напрямлені вниз, яка має вершину в точці (3; 1) і симетрична відносно прямої 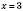 .
.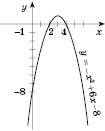
Зверніть увагу: будь-яка парабола має один проміжок зростання й один проміжок спадання, причому вісь Ox розбивається на ці проміжки точкою, яка відповідає точці xв.
Розв’язування квадратних нерівностей за допомогою графіків
Якщо лівою частиною нерівності є вираз виду 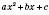 , де
, де 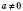 , b, c – дані числа, а правою – нуль, то таку нерівність називають Квадратною нерівністю.
, b, c – дані числа, а правою – нуль, то таку нерівність називають Квадратною нерівністю.
Квадратні нерівності зручно розв’язувати за допомогою графіків квадратичних функцій.
Для цього треба:
1) знайти корені тричлена 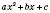 або з’ясувати, що їх немає;
або з’ясувати, що їх немає;
2) зобразити схематично графік функції 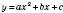 , звертаючи увагу тільки на точки перетину з віссю Ox і напрям віток параболи залежно від знака коефіцієнта а;
, звертаючи увагу тільки на точки перетину з віссю Ox і напрям віток параболи залежно від знака коефіцієнта а;
3) знайти на осі Ox проміжки, для яких виконується дана нерівність.
Приклади
1) 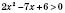 ,
, 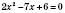 ,
, 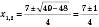 ,
,
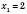 ,
, 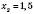 .
.
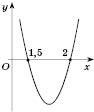
На ескізі графіка функції 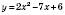 (див. рисунок) знайдемо проміжки, на яких
(див. рисунок) знайдемо проміжки, на яких 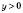 .
.
Відповідь: 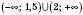 .
.
2) 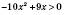 ,
,
 ,
,
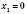 ,
, 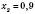 .
.
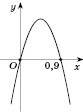
Вітки параболи графіка напрямлені вниз (див. рисунок).
Відповідь: (0; 0,9).
3) 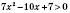 ,
,
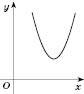
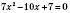 ,
,
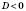 – коренів немає.
– коренів немає.
Графік функції не перетинає вісь абсцис (див. рисунок).
Відповідь: 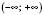 .
.
4) 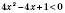 ,
,
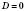 ,
, 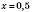 .
.
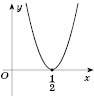
Графік перетинає вісь абсцис в одній точці (див. рисунок).
Відповідь: 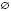 .
.
5) 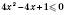 .
.
Відповідь: 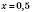 .
.
6) 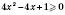 .
.
Відповідь: 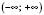 .
.
7) 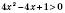 .
.
Відповідь: 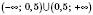 .
.
Дуже зручно користуватися таким простим правилом: квадратний тричлен із додатним першим коефіцієнтом набуває додатних значень “за коренями”, а від’ємних – “між коренями”; і навпаки: квадратний тричлен з від’ємним першим коефіцієнтом набуває додатних значень “між коренями”, а від’ємних – “за коренями”.
Рівняння, що зводяться до квадратних
Рівняння виду 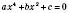 , де
, де 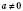 , називається Біквадратним.
, називається Біквадратним.
Для його розв’язання вводять нову змінну:
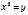 ,
, 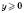 .
.
Приклади
1) 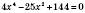 .
.
Нехай 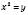 ,
, 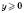 .
.
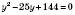 . Розв’язавши це квадратне рівняння, знайдемо:
. Розв’язавши це квадратне рівняння, знайдемо:
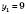 ,
, 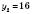 .
.
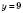 ,
, 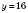 ,
,
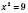 ,
, 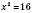 ,
,
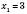 ,
, 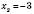 .
. 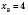 ;
; 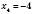 .
.
Відповідь: 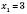 ,
, 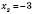 ,
, 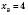 ,
, 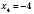 .
.
2) 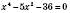 .
.
Нехай 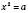 ,
, 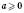 .
.
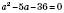 ,
,
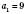 ,
, 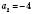 не задовольняє умову
не задовольняє умову 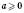 .
.
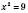 ,
,
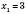 ,
, 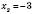 .
.
Відповідь: 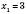 ,
, 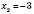 .
.
3) 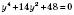 .
.
Нехай 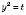 ,
, 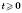 .
.
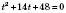 ,
,
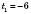 ;
; 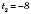 .
.
t1 і t2 не задовольняють умову 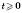 .
.
Відповідь: коренів немає.
Введення нової змінної дає можливість звести до квадратних і деякі інші види рівнянь.
Приклади
1. 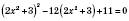 .
.
Нехай 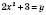 ,
, 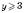 .
.
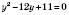 ,
,
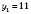 ,
, 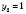 не задовольняє умову
не задовольняє умову 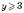 .
.
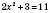 ,
,
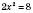 ,
,
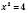 ,
,
 .
.
Відповідь: 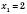 ,
, 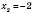 .
.
2. 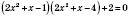 .
.
Нехай 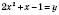 .
.
Тоді 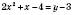 ,
,
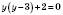 ,
,
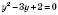 ,
,
Відповідь: 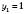 ,
, 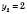 .
.
а) 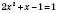 .
.
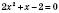 ,
,
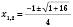 ,
,
Відповідь: 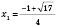 ,
, 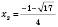 .
.
б) 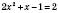 .
.
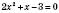 ,
, 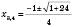 ,
,
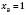 ;
; 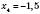 .
.
Відповідь: 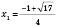 ,
, 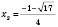 ,
, 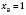 ,
, 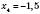 .
.