Лінійна функція, її графік і властивості
849. Лінійною функцією є:
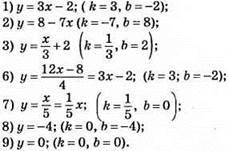
850. Прямою пропорційністю є функції:
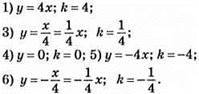
851. y = 6x – 5
X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
У | -23 | -17 | -11 | -5 | 1 | 7 | 13 |
852. 1) y = -2x + 5
Якщо x = -4, то у = -2 • (-4) + 5 = 13.
Якщо x = 3,5, то у = -2 • 3,5 + 5 = -2.
Якщо x = 0, то у = -2 • 0 + 5 = 5.
2). y = 9; -2х + 5 = 9; -2x = 9 – 5; -2x = 4; х = 4 : (-2); х = -2;
У = -5; -2х + 5 = -5; -2x = -5 –
Y = 0; -2х + 5 = 0; -2х = -5; х = -5 : (-2); x = 2,5.
853. y = 0,3х – 2
1) Якщо х = 5, то у = 0,3 • 5 – 2 = -0,5.
Якщо x = -2, то у = 0,3 • (-2) – 2 = -2,6.
Якщо х = 0, то у = 0,3 • 0 – 2 = -2.
2) у = 1; 0,3x – 2 = 1; 0,3x = 3; x = 10;
Y = -11; 0,3x – 2 = -11; 0,3x = -11 + 2; 0,3x = -9; x = -30;
У = 0,8; 0,3x – 2 = 0,8; 0,3x = 0,8 + 2; 0,3x = 2,8; x = 9•1/3.
854. 1) y = x – 5
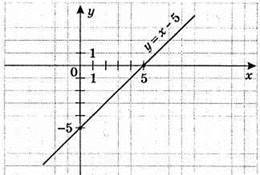
X | 0 | 5 |
У | -5 | 0 |
2) y = 3x + 1
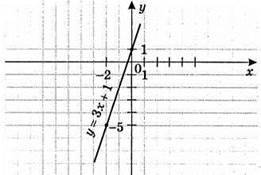
X | 0 | -2 |
Y | 1 | -5 |
3)
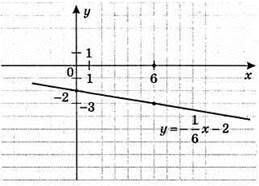
X | 0 | 6 |
Y | -2 | -3 |
4) y = 0,4x + 3
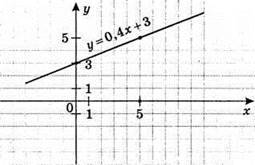
X | 0 | 5 |
Y | 3 | 5 |
855. Розв’язання. Складемо таблицю значень даної функції для двох довільних значень аргументу:
1) y = 4 – х
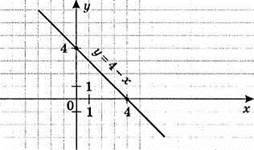
X | 0 | 4 |
Y | 4 | 0 |
2) у = -4x + 5
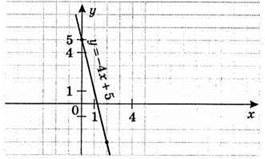
X | 0 | 1 |
Y | 5 | 1 |
3) у = 0,2x – 3
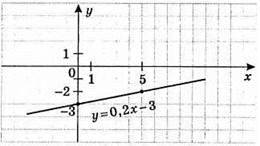
Х | 0 | 5 |
Y | -3 | -2 |
856. 1) y = 1/3x
X | 6 | -3 | -3,2 |
Y | 2 | -1 | -16/15 |
2) x = 3у
Х | -6 | 1 | 36 |
Y | -2 | 1/3 | 12 |
857. 1) y = 1,2x
X | 10 | 0,6 | -5 | -4 |
Y | 12 | 0,72 | -6 | -4,8 |
2) х = у : 1,2
X | 3 | -2 | 5 |
Y | 3,6 | -2,4 | 6 |
858. 1) у = 3x
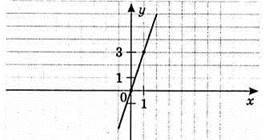
X | 1 |
Y | 3 |
2) у = -2х
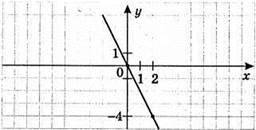
X | 2 |
Y | -4 |
3) у = -0,6x
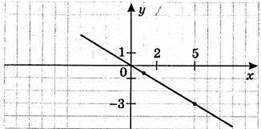
X | 5 |
Y | -3 |
4) y = 1/7x
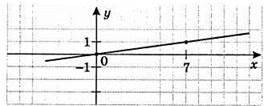
X | 7 |
Y | 1 |
859. 1) y = 5x
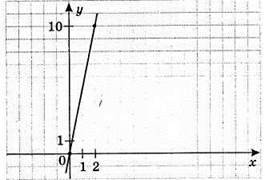
X | 2 |
Y | 10 |
2) у = 0,8х
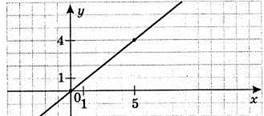
X | 5 |
Y | 4 |
3) у = -1/6х
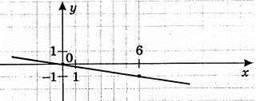
X | 6 |
Y | -1 |
860. 1)
X | 8 | 6 | 2 | 1 | 1/2 | 0 | -1 | -2 | -3 | -4 |
Y | 4 | 3 | 1 | 1/2 | 1/4 | 0 | -1/2 | -1 | -1,5 | -2 |
2) y = 1/2x.
3)
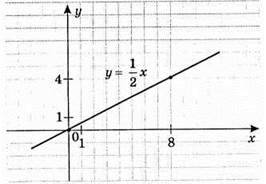
861.
862. у = 2х – 3
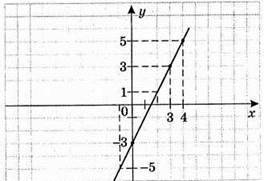
X | 0 | 3 |
Y | -3 | 3 |
1) якщо х = 4, то у = 5; якщо х = -1, то у = -5; якщо х = 0,5, то у = -2;
2) у = 1 при х = 2; у = -1 при х = 1; у = 0 при х = 1,5;
3) функція набуває додатних значень при х > 1,5.
863. у = 2 – 4х
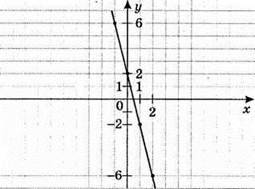
X | 0 | 1 |
Y | 2 | -2 |
1) якщо х = 1, то у = -2; якщо х = 0, то у = 2; якщо х = -2, то у = 10;
2) у = -4 при х = 1,5; у = -2 при x = 1; y = 2 при х = 0;
3) функція набуває від’ємних значень при х > 0,5.
864. y = 0,5x
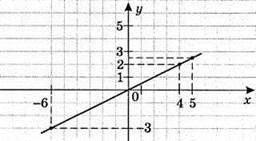
X | 4 |
Y | 2 |
1) якщо х = 4, то у = 2; якщо х = -6, то у = -3; якщо х = 3, то у = 1,5;
2) у = 2,5 при х = 5; y = -2 при х = -4; у = 1 при х = 2;
3) функція набуває від’ємних значень при х < 0.
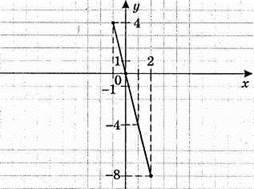
865. y = – 4х
X | 2 |
Y | -8 |
1) якщо х = 2, то у = -8; якщо х = -1, то у = 4; якщо х = 0,5, то у = -2;
2) y = -4 при х = 1; у = 2 при х = -0,5;
3) функція набуває додатних значені, при х < 0.
866. y = 1,8х – 3
Через А(-2; -6,6) графік проходить, бо -6,6 = 1,8 • (-2) – 3 – правильна рівність;
Через В(1; 1,2) графік не проходить, бо 1,2 = 1,8 • 1 – 3 – неправильна рівність;
Через С(0; -3) графік проходить, бо -3 = 1,8 • 0 – 3 – правильна рівність;
Через D(5; 7); графік не проходить, бо 7 = 1,8 • 5 – 3 – неправильна рівність.
867. y = 8х – 14
1) А(-1; -6) не належить графіку даної функції, бо -6 = 8 • (-1) – 14 – неправильна рівність;
2) В(2; 2) належить графіку даної функції, бо 2 = 8 • 2 – 14 – правильна рівність;
868. у = х – 1
X | 0 | 4 |
У | -1 | 3 |
Y = 1/4x + 2
X | 4 | 0 |
Y | 3 | 2 |
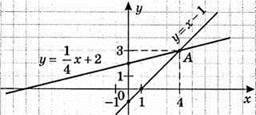
А(4; 3) – точка перетину графіків даних функцій.
869. у = 5x – 6
X | 0 | 2 |
Y | -6 | 4 |
У = -2x + 1
X | 0 | -2 |
Y | 1 | 5 |
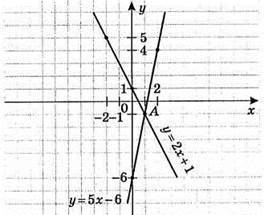
А(1; -1) – точка перетину графіків даних функцій.
870. 1) y = 2,5x + 10
Точка перетину з віссю x: 2,5x + 10 = 0; 2,5x = -10; x = -10 : 2,5; x = -4; (-4; 0).
Точка перетину з віссю у: (0; 10).
2) у = 6x – 4
Точка перетину з віссю x: 6x – 4 = 0; 6x = 4; x = 4 : 6; x = 2/3; (2/3; 0).
Точка перетину з віссю у: (0; -4).
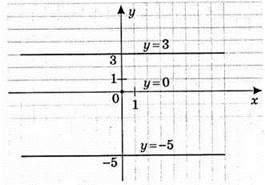
871. 1) 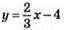
X = 0: у = -4; (0; -4) – точка перетину графіка функції з віссю у;
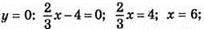 (6; 0) – точка перетину графіка функції з віссю x.
(6; 0) – точка перетину графіка функції з віссю x.
2) у = 7 – 3x
X = 0: у = 7; (0; 7) – точка перетину графіка функції з віссю у;
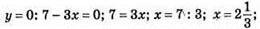
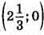 – точка перетину графіка функції з віссю х.
– точка перетину графіка функції з віссю х.
872. у = 2х – 9
1) x = у; 2x – 9 = x; 2x – x = 9; x = 9; (9; 9).
2) у = х + 6; 2x – 9 = x + 6; 2x – x = 6 + 9; x = 15; y = 15 + 6 = 21; (15; 21).
873. у = -7x + 8
У = – x; – x = -7x + 8; – x + 7x = 8; 6x = 8; x = 4/3; y = -4/3; (4/3; -4/3), або 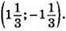
874. 1) y = 3,7x +10 і у = 1,4x – 13;
3,7x + 10 = 1,4x – 13; 3,7x – 1,4x = -13 – 10;
2,3x = -23; x = -23 : 2,3; x = -10; у = 3,7 • (-10) + 10 = -37 + 10 = -27.
(-10; -27) – точка перетину графіків даних функцій.
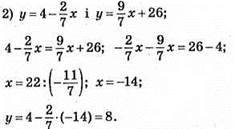
(-14; 8) – точка перетину графіків даних функцій.
875. у = 4x – 7 і у = -2х + 11;
4x – 7 = -2x + 11; 4x + 2x = 11 + 7; 6x = 18; x= 18 : 6; x = 3;
У = 4 • 3 – 7 = 5; (3; 5) – точка перетину графіків даних функцій.
876. f(x) = 4x – 3 і g(x) = 3x – 2; 4x – 3 = 3x – 2; 4x – 3x = -2 + 3; x = 1.
F(x) = 4 • 1 – 3 = 1. При x = 1 функції набувають різних значень.
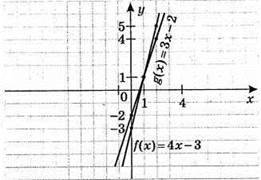
F(x) = 4x – 3
X | 0 | 2 |
Y | -3 | 5 |
G(x) = 3x – 2
X | 0 | 2 |
У | -2 | 4 |
1) f(x) > g(x) при x > 1; 2) f(x) < g(x) при x < 1.
877. f(x) = 5 – 2х і g(x) = 2x – 3
5 – 2х = 2х – 3; -2х – 2х = -3 – 5; -4х = -8; х = -8 : (-4); х = 2.
При х = 2 функції набувають рівних значень.
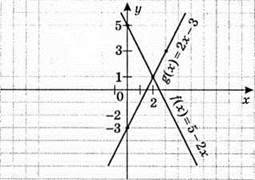
F(x) = 5 – 2х
X | 0 | 2 |
У | 5 | 1 |
G(x) = 2x – 3
X | 0 | 3 |
Y | -3 | 3 |
1) f(x) < g(x) при х > 2;
2) f(x) > g(x) при х < 2.
878. y = kx. M(2; -5), 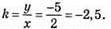
Отже, функція задається формулою у = -2,5х.
879. 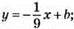 А(-27; 4) – лежить на графіку.
А(-27; 4) – лежить на графіку.
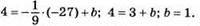
Отже, 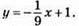
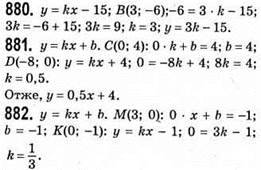
Отже, 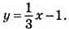
883. у = kx + b. y = -6, тоді при x = 0 у = -6. Звідси b = -6.
Y = kx – b, у = -6 при будь-яких x.
Тоді kx – 6 = -6; kx = 0; ft = 0.
Отже, і/ = -6, тобто ft = 0, b = -6.
884. Якщо графік паралельний осі абсцис, то всі точки графіка мають однакову ординату. Оскільки т. А(-2; 3) лежить на графіку, то всі точки мають ординату 3. Тоді b = 3. у = kx + 3; оскільки у = 3, то kx + 3 = 0; k = 0.
Отже, у = 0х + 3, або у = 3. k = 0; b = 3.
885. Розв’язання.
1) 36 а) – процес витікання;
36 б) – процес наповнення бака водою.
2) а) 50 л; б). 10 л;
3) а) 40 л; б) 15 л;
4) а) через 4 хв; б) через 8 хв.;
5) наливається щохвилини 2,5 л води, виливається щохвилини 5 л води;
6) у = 50 – 5х; у = 10 + 2,5х.
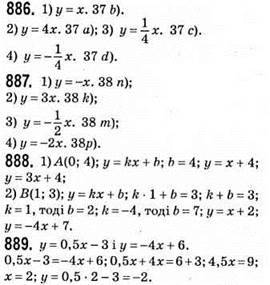
(2; -2) – точка перетину графіків.
У = kх; -2 = k • 2; k = -1; у = – х
890. 1,5х – 3 = 2,5х + 1. – х = 4; х = -4; у = 1,5 • (-4) – 3 = -9.
(-4; -9) – точка перетину графіків.
У = 5х + b проходить через точку (-4; -9).
5 • (-4) + b = -9; b = -9 + 20; b = 11; у = 5х + 11; b = 11.
891.
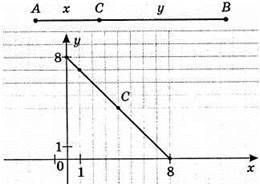
У = 8-х
Точка С відповідає випадку, коли С – середина АВ.
892. Р = 12, тоді АВ + AD = 6. у = 6 – х. Точка А відповідає випадку, коли ABCD – квадрат, тобто х = у.
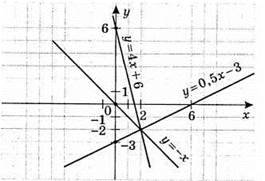
893. Побудуємо графіки функцій:
1)
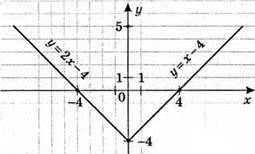
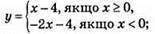
2)
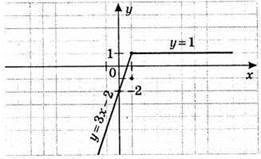
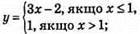
3)
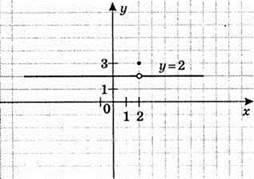
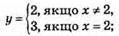
4)
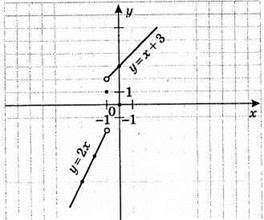
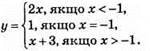
894. 1) 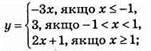
2) рис.
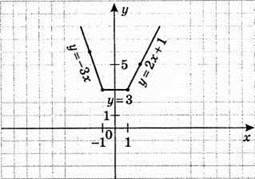
895. 1) y = |х|.
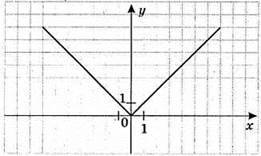
Якщо х ≥ 0, то у = х; якщо х < 0, то у = – х.
2) у = |х| + x.
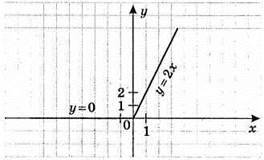
Якщо х ≥ 0, то у = 2х; якщо х < 0, то у = 0.
3) у = 4x – |х| + 2.
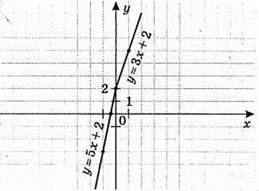
Якщо х ≥ 0, то у = 3х + 2; якщо х < 0, то у = 5х + 2.
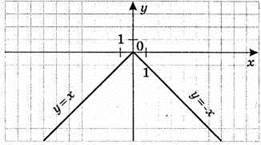
896. 1) у = -|х|. Якщо х ≥ 0, то у = – х; якщо х < 0, то у = х.
3) у = 3x + 2|x|.
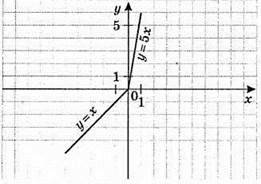
Якщо х ≥ 0, то у = 5х; якщо х < 0, то y = х.
897. 1) Пряма a: у = х + 3.
2) Пряма b: у = -0,5х – 1.
898. 1) Пряма m: у = -2/3х.
2) Пряма n: у = 2,5х – 5.
899. f(х) = х – [х].
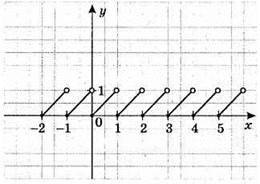
900. 1) Якщо а = -1,5, то 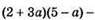
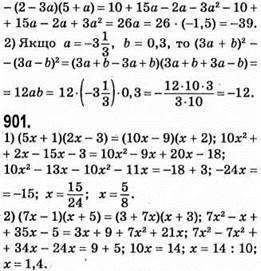
902. Нехай х, х + 1, х + 2 – шукані числа. Тоді
X3 + (x + 1)3+ (x + 2)3 = x3 + x3 + 3×2 + 3x + 1 + x3 + 6×2 + 12x + 8 = 3×3 + 9×2 + 15x + 9 = 3 • (x3 + 3×2 + 5x + 3); ділиться наділо на 3, бо 3 ділиться на 3.
903. Нехай у І і у II бочках було по х л води. Тоді у І бочці після збільшення стало 1,1x л води, після зменшення стало 1,1x – 0,1 • 1,1х = 1,1х – 0,11х = 0,99х л води. У II бочці після зменшення стало 0,9x л води, після збільшення стало 0,9x + 0,1 • 0,9x = 0,99x л води. 0,99x = 0,99x. Отже, в обох бочках води стало порівну.
904. х4 + х2у2 + у4 = x4 + 2х2у2 + у4 – х2у2 = (x2 + у2)2 – (ху)2 = а2 – b2.
905. |x| ≥ x при будь-якому значенні x, тоді |x| – x ≥ 0.
2х – x2 – 2 = – х2 + 2х – 1 – 1 = -(x2 – 2x + 1) – 1 = -(x – 1)2 – 1.
-(x – 1)2 – 1 < 0 при будь-якому значення x, тоді |x| – x > -(x – 1)2 – 1 при будь-якому значенні x, бо будь-яке додатне число більше будь-якого від’ємного.
906. 1) Якщо x = -4, у = 0,6, то 0,1x + 5y = 0,1 • (-4) + 5 • 0,6 = -0,4 + 3 = 2,6.
2) Якщо x = 6, у = -2, то х2 – 3y + 7 = 62 – 3 • (-2) + 7 = 36 + 6 + 7 = 49.
3) Якщо x = -10, у = 2, то |x| + |у – 6| = |-10| + |2 – 6|= 10 + 4 = 14.
4) Якщо x = -4, у = 1,5, то (2у – 3)2 – (x + 4)2 = (2y – 3 – x – 4)(2у – 3 + x + 4) = (2у – х – 7)(2у + x + 1) = (2 • 1,5 + 4 – 7)(2 • 1,5 – 4 + 1) = 0 • 0 = 0.
907. 1) x = -3; у – довільне число;
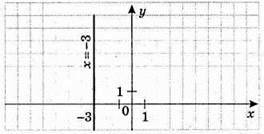
2) у = 2; х – довільне число;
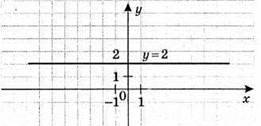
3) x = 0; у – довільне число.
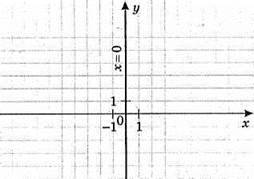
Цій умові відповідають усі точки, які лежать на осі у.