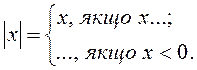Лінійне рівняння з двома змінними та його графік
Урок № 70
Тема. Лінійне рівняння з двома змінними та його графік
Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння виконувати рівносильні перетворення рівнянь із двома змінними.
Тип уроку: засвоєння знань, умінь та навичок.
Хід уроку
I. Організаційний
II. Перевірка домашнього завдання
@ Під час самоперевірки за зразком з’ясовуємо основні моменти в розв’язаннях завдань № 2; 3; 4.
Бажаючі учні готують презентацію складених ними алгоритмів. Після презентації проводиться перевірка та корекція.
III. Формулювання мети й завдань уроку
@ Можна залучати до цього учнів, якщо звернутись до спостережень, що були здійснені у ході виконання № 4 з домашнього завдання, а саме: рівняння із двома змінними мають дуже схожий вигляд (як описати його?), графіки їх рівнянь також мають однаковий вид – прямі (ми знаємо, що пряма є також графіком лінійної
IV. Актуалізація опорних знань
Запитання до класу (“Мікрофон” або ігровий момент “Найрозумніший”)
1. Що називається розв’язком рівняння з двома змінними?
2. Чи є пара чисел (4; 1) розв’язком рівняння х – 2у = 2?
3. Що називається графіком рівняння з двома змінними? Чи завжди таке рівняння має графік?
4. Які рівняння із двома змінними називаються рівносильними? Яку властивість мають графіки рівносильних рівнянь?
5. Серед даних рівнянь із двома змінними виберіть пари таких, що мають однакові графіки, та поясність, чому ви так вважаєте:
1) х + у = 2;
2) у = х + 2;
3) у =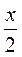 
;
4) 2у = х;
5) у = – х + 2.
V. Вивчення нового матеріалу
@ Узагальнивши вид рівнянь із двома змінними, що подаються в № 4 домашнього завдання, формулюємо означення лінійного рівняння з двома змінними (звертаємо увагу на фразу “рівняння виду”, що означає рівняння, яке можна записати в такому вигляді).
Після цього з’ясуємо вид графіка лінійного рівняння: якщо хоча б один з коефіцієнтів а або b рівняння ax + by + c = 0 не дорівнює 0, шляхом тотожних перетворень лінійне рівняння приводимо до вигляду y = kx + b і робимо висновок: графік лінійного рівняння збігається в цьому випадку із графіком лінійної функції, тобто є прямою. Розглядаючи приклади на побудову графіків лінійних рівнянь із двома змінними, звертаємо увагу учнів на те, що графік лінійного рівняння (якщо хоча б один із коефіцієнтів а або b не дорівнює 0) можна будувати за двома точками. Іноді за такі точки беруться точки перетину графіка з координатними осями (якщо ці точки не дуже віддалені від початку координат або, навпаки, не дуже близько розташовані від початку координат).
VI. Закріплення знань. Вироблення вмінь
Виконання усних вправ
1. Серед поданих рівнянь назвіть лінійні рівняння з двома невідомими:
1) ху = 3;
2) х + 2у = 7;
3) х + у2 = 4;
4) х – у = 1;
5) 12х + 10у = 0;
6) 0х – 2у = 3;
7) 3х + 0у = 0;
8) 0х + 0у = 0;
9) 0х + 0у = 1.
2. Назвіть кілька розв’язків лінійного рівняння 0,5х – у = 1.
3. Як на координатній площині розташований графік рівняння:
1) х = -2;
2) у = 7;
3) 5 – х = 0;
4) 2х – 1 = 0?
Виконання письмових вправ:
1. Які з пар чисел (2; 2); (1; 3); (1; 3,5); (4; -1);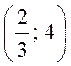 
Є розв’язками рівняння 3х + 2у = 10?
2. Виразіть у через х у рівняннях та знайдіть два які-небудь розв’язки рівнянь:
1) х – у = 7; 2) 3х + 2у = 5.
3. Які з точок К(2; 0,5); L(0; 2); M(2; 4); N(3; 0,25) не належать графіку рівняння -3х + 4у = 8?
4. Побудуйте графік рівняння:
1) x – 3у = 6;
2) x – 2у = 0;
3) 1,5х = 6;
4) -0,3у = 0,6;
5) 5х – 6у = 4;
6) 8х + 16у = 24.
5. На прямій, яка є графіком рівняння 4х + 9у = 1, узяли точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.
6. Знайдіть значення коефіцієнта а в рівнянні ах + 3у = 4, якщо відомо, що графік рівняння проходить через точку (1; 2). Побудуйте графік рівняння.
VII. Підсумки уроку
Контрольні запитання
1. Яке рівняння з двома змінними називається лінійним? Наведіть приклад такого рівняння.
2. Яка фігура є графіком лінійного рівняння ах + bу = с, в якому хоча один з коефіцієнтів а чи b не дорівнює сумі? Як розташований в координатній площині графік рівняння х = m; у = n?
VII. Домашнє завдання
№ 1. Вивчіть зміст нових понять уроку.
№ 2. Виразіть у через х у рівнянні та знайдіть два будь-які розв’язки рівняння:
1) 5х – 2у = 8;
2) 2х – 5у = 7;
3) 3х + 2у = 10.
№ 3. (Пара чисел) точка (є розв’язком рівняння) належить графіку рівняння 2х + bу = 12. Знайдіть b та побудуйте графік рівняння.
№ 4. В одній системі координат побудуйте графіки рівнянь:
1) х + у = 2;
2) – х – у = -2;
3) 2х + 7у = 4.
Чому графіками цих рівнянь є одна й та сама пряма?
№ 5. Повторіть означення модуля числа. Закінчіть запис:
(1 votes, average: 5.00 out of 5)
Loading...