Логарифмічна функція, її графік і властивості
УРОК 56
Тема. Логарифмічна функція, її графік і властивості
Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком.
І. Перевірка домашнього завдання
1. Три учні відтворюють розв’язування вправ № 13, 15, 20.
2. Розв’язування вправ, аналогічних домашнім.
А) Обчисліть: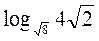 
; 
.
=
=
=
=
=
–
=
=
==
=–
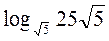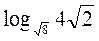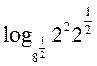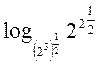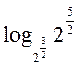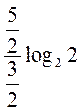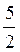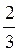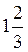
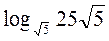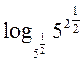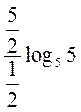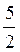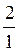= 5.
Б) Обчисліть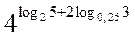 
.
=
=
=
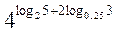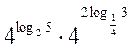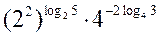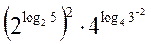= 52 – 3-2 = 25 – 
= 
= 
.
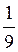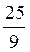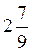II. Аналіз самостійної роботи, проведеної на попередньому уроці
III. Засвоєння властивостей логарифмічної функції та її графіка
Функція виду у = loga x, де а – задане число, а > 0, а? 1 називається логарифмічною функцією.
Логарифмічна
1) Область визначення функції – множина всіх додатних чисел. Ця властивість випливає із означення логарифма, оскільки вираз loga х має смисл тільки при х > 0.
2) Область значень логарифмічної функції – множина R усіх дійсних чисел. Ця властивість випливає з того, що для будь-якого дійсного числа b є таке додатне число х, що loga x = b, тобто рівняння loga x = b має єдиний корінь. Такий корінь існує і дорівнює х = аb, оскільки loga аb = b.
3) Логарифмічна функція на всій області визначення зростає (при а > 1) або спадає (при 0 < а < 1). Нехай а > 1. Доведемо, що якщо x2 > х1 > 0, то
Loga х2 > loga x1. Користуючись основною логарифмічною тотожністю, умовою x2 > х1, можна записати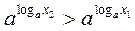 
. З останньої нерівності за властивістю степеня з основою а > 1 маємо, що loga х2 > loga x1.
Нехай 0 < а < 1. Доведемо, що якщо x2 > х1 > 0, то loga х2 < loga x1. Записавши умову x2 > х1 у вигляді 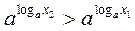одержуємо loga х2 < loga x1, оскільки 0 < а < 1.
4) Якщо а > 1, то функція у = loga x приймає додатні значення при х > 1, від’ємні – при 0 < х < 1. Якщо 0 < а < 1, то функція у = loga x приймає додатні значення при 0 < х < 1, від’ємні – при х > 1.
Ця властивість випливає з того, що функція у = loga x приймає значення, рівне нулю, при х = 1 і є зростаючою на проміжку х > 0, якщо а > 1, і спадною, якщо 0 < а < 1. Спираючись на доведені властивості, неважко побудувати графік функції у = loga x (рис. 163).
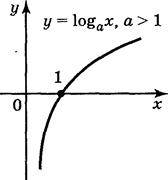
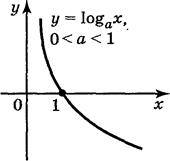
Рис. 163
Графіки показникової функції і логарифмічної функції, які мають однакові основи, симетричні відносно прямої у = х (рис. 164), бо функції у = 0х і у = loga x є взаємнооберненими.
IV. Осмислення властивостей логарифмічної функції
1. Усне виконання вправ № 37-39, 40.
2. Письмове виконання вправ № 46, 50.
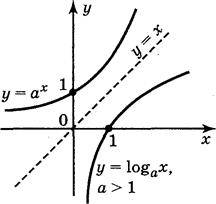
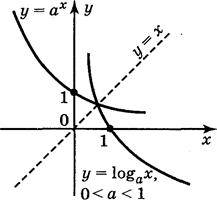
Рис. 164
V. Систематизація вивченого матеріалу
Повторення властивостей логарифмічної функції і заповнення таблиці 23.
1. D(y) = …. 2. Е(у) = …. | |
A > 1 3. Якщо х1 < x2 то ………………….. 4. loga x > 0, якщо….. Loga х = 0, якщо….. Loga x < 0, якщо….. | 0 < а < 1 3. Якщо х1 < x2 то ………………….. 4. loga x > 0, якщо….. Loga х = 0, якщо….. Loga x < 0, якщо….. |
VI. Підведення підсумків уроку
VII. Домашнє завдання
Розділ V § 2. Запитання і завдання для повторення до розділу V № 15-25. Вправи № 44, 49.
(1 votes, average: 5.00 out of 5)
Loading...