Медіана, бісектриса і висота трикутника
Урок № 24
Тема. Медіана, бісектриса і висота трикутника
Мета: домогтися засвоєння учнями:
– змісту понять “медіана трикутника”; “бісектриса трикутника”; “висота трикутника”;
– уявлення про положення висот у різних видах трикутника.
Сформувати вміння:
– зображати медіани, висоти та бісектриси трикутника;
– розрізняти ці відрізки, виходячи з умови задачі.
Тип уроку: застосування знань, умінь та навичок.
Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця
Таблиця
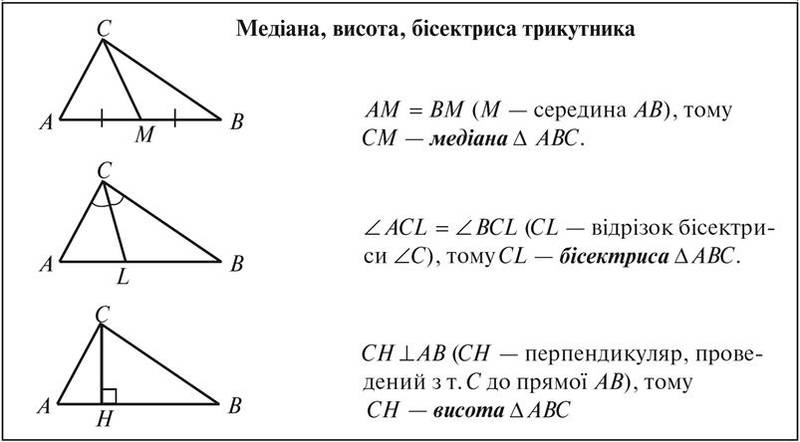
ХІД УРОКУ
I. Організаційний момент
II. Перевірка домашнього завдання
Самостійна робота
Варіант 1
1. Основа рівнобедреного трикутника в 2 рази менша від його бічної сторони, а периметр дорівнює 15 см. Знайдіть сторони трикутника.
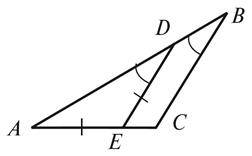
2. У трикутнику ABC (рис. 1) AE = DE;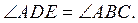 
Доведіть, що Δ ABC – рівнобедрений.
Варіант 2
1. Периметр рівнобедреного трикутника дорівнює 14 см, а його бічна сторона в 3 рази більша за основу. Знайдіть сторони трикутника.
2. У трикутнику
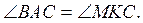Доведіть, що ΔKMC – рівнобедрений.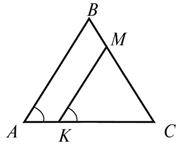
Відповіді:
Варіант 1. 1. Основа 3 см; бічні сторони по 6 см.
Варіант 2. 1. Основа 2 см; бічні сторони по 6 см.
III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку
На цьому етапі вивчення геометрії єдино можливим варіантом мотивації можуть бути слова вчителя про існування деяких інших (окрім сторін та кутів) елементів трикутника та важливість їхніх властивостей для розв’язування задач.
Виходячи зі сказаного вчителем, основну мету формулюємо як вивчення означень та формування вмінь використовувати означення нових елементів для розпізнавання та побудови “нових” елементів трикутника.
IV. Актуалізація опорних знань
Виконання усних вправ
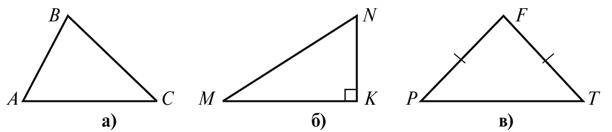
На рисунку 3:
А) назвіть елементи кожного з трикутників;
Б) визначте вид трикутників за сторонами;
В) вкажіть найбільший кут у кожному трикутнику, визначте його вид.
Як тепер можна назвати кожний з трикутників?
V. Засвоєння нових знань
План вивчення нового матеріалу
1°. Означення медіани трикутника. Властивості медіан.
2°. Означення бісектриси трикутника. Властивості бісектрис.
3°. Означення висоти трикутника. Властивості висот.
4°. Положення висоти в різних видах трикутників.
5°. Взаємне розташування висоти, медіани та бісектриси, проведених з однієї вершини трикутника.
VI. Первинне усвідомлення нового матеріалу
Виконання усних вправ
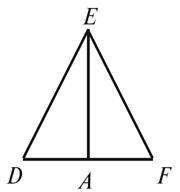
1. У трикутнику DEF проведено відрізок EA (рис. 4). Визначте, чи є цей відрізок медіаною, бісектрисою або висотою даного трикутника, якщо:
А) DA = FA;
Б)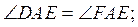 
В)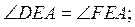 
Г) DE = FE і DA = FA.
2. Чи може лежати всередині трикутника тільки одна з трьох його висот; тільки дві з трьох його висот?
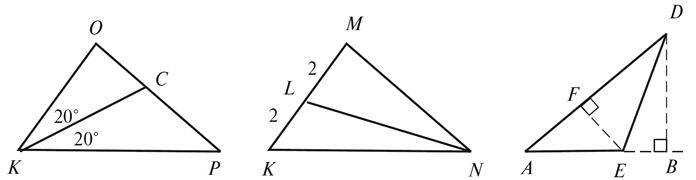
3. Назвіть, чим є відрізки KC, NL, EF і DB для зображених на рисунку 5 трикутників KOP, MNK і ADE.
4. У трикутнику ABC проведено бісектрису BK та медіану BM. Відомо, що AC = 8 см;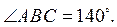 
Знайдіть довжину відрізка AM та градусну міру кута ABK.
Виконання графічних вправ
1. Накресліть три трикутники – гострокутний, тупокутний і прямокутний. Використовуючи косинець, проведіть у кожному з них висоту з вершини гострого кута.
2. Накресліть довільний трикутник. Скільки медіан можна в ньому провести? Побудуйте їх, використовуючи лінійку з поділками.
Виконання письмових вправ
Рівень А
1. У рівнобедреному трикутнику ABC відрізок BD-медіана, проведена до основи. Знайдіть периметр трикутника ABC, якщо PΔ ABD =12 см, BD = 4 см.
2. У трикутнику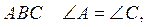 
BD – бісектриса трикутника. Доведіть, що AD = CD.
Рівень Б
Доведіть, що в рівнобедреному трикутнику медіани, проведені до бічних сторін, рівні.
Рівень В
Доведіть рівність трикутників за стороною, прилеглим кутом і бісектрисою, проведеною з вершини цього кута.
Письмову задачу 2 можна розв’язати вже на цьому уроці як пропедевтичну для теореми про властивість медіани рівнобедреного трикутника, що проведена до основи, а потім розв’язати її на наступному уроці після ознайомлення учнів з теоремою і порівняти розв’язання задачі з доведенням теореми.
VII. Підсумки уроку
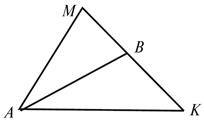
Зробіть необхідні позначки на рисунку, щоб відрізок AB був зображенням:
А) медіани;
Б) висоти;
В) бісектриси трикутника.
VIII. Домашнє завдання
1. Накресліть нерівнобедрений трикутник ABC.
А) Позначте точку M – середину сторони BC. Проведіть відрізок AM. Як він називається?
Б) Проведіть бісектрису кута B і позначте точку L її перетину зі стороною AC. Як називається відрізок BL?
В) Проведіть із точки C перпендикуляр CH до прямої AB. Як називається побудований відрізок у трикутнику ABC?
2. У рівнобедреному трикутнику ABC відрізок BD-медіана, проведена до основи. Знайдіть периметр трикутника BDC, якщо PΔ ABC = 18 см, BD = 5 см.
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.
(1 votes, average: 5.00 out of 5)
Loading...