Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Метод геометричних місць

Метод геометричних місць

Урок № 48

Тема. Метод геометричних місць

Мета: домогтися засвоєння учнями схеми дій, що покладено в основу методу геометричних місць.

Сформувати вміння:

– відтворювати схему, що лежить в основі методу геометричних місць;

– виконувати дії, що передбачені цією схемою.

Тип уроку: засвоєння знань, умінь та навичок.

Наочність і обладнання: набір демонстраційного креслярського приладдя.

ХІД УРОКУ

I. Організаційний момент

II. Перевірка домашнього завдання

Виконання усних вправ перевіряємо під час фронтальної

бесіди, письмових вправ – за зразком.

III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку

Для мотивації пропонуємо учням виконати завдання:

1) знайдіть ГМТ, рівновіддалених від точок A і B;

2) знайдіть ГМТ, віддалених від точок A і B на певну відстань a;

3) знайдіть ГМТ, рівновіддалених від точок A, B, C (точки A, B, C не лежать на одній прямій).

Порівняння умов запропонованих завдань приводить до формулювання проблеми, яку треба розв’язати: як побудувати геометричне місце точок, які задовольняють одночасно дві (а не одну) умови?

Пошук відповіді на це питання і є основною дидактичною

метою уроку.

IV. Засвоєння нових знань

Міркування, що лежать в основі методу геометричних місць є досить простими і зрозумілими учням. Викладення цих міркувань учитель може проводити індуктивним або дедуктивним методом, тобто на прикладі однієї із запропонованих на третьому етапі задач продемонструвати хід міркувань, а потім узагальнити ці міркування або навпаки-сформулювавши загальні твердження, потім розглянути приклади його застосування.

VI. Первинне усвідомлення нового матеріалу

Виконання письмових вправ

В умовах наступних задач усно виділити дві умови, які повинні задовольняти шукане ГМТ.

1. Точки A, B, C не лежать на одній прямій. Побудуйте точку, рівновіддалену від точок A, B, C.

Відповідь. Шукана точка, по-перше, рівновіддалена від точок A і B, по-друге, рівновіддалена від точок B і C.

2. Дано точки A, B, C. Побудуйте точку, яка рівновіддалена від точок A і B і лежить на заданій відстані від точки C.

3. Побудуйте точку, рівновіддалену від сторін даного кута, яка лежить на відстані d від його вершини.

4. Точка A лежить на колі радіуса R. Побудуйте точки даного кола, віддалені від точки A на відстань R.

Після виконання такого аналізу умов задач, починаємо письмове розв’язання задач № 1 і № 3.

VII. Підсумки уроку

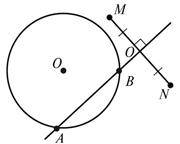
За рисунком сформулюйте задачу, розв’язком якої є точки A і B.

Метод геометричних місць

VIII. Домашнє завдання

Розв’язати задачі № 2, 4 класної роботи.

Розв’язати методом геометричних місць задачу.

Задача. Знайдіть геометричне місце центрів кіл радіуса R, що проходять через дану точку A.

Джерела:

1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Розв’язування задач геометричного змісту Урок № 126 Тема. Розв’язання задач геометричного змісту 1. На координатній прямій позначте точку D(-3) і точку С, щоб довжина CD дорівнювала 2,5 одиничних відрізки. Визначте координату точки С. Скільки розв’язків має задача? 2. Знайдіть площу і периметр чотирикутника ABCD, якщо A(-1; 2); B(3; 2); С(3; -4); D(-1; -4). 3. Знайдіть площі заштрихованих фігур, зображених […]...

  2. Тематичне оцінювання № 5 Урок 52 Тема. Тематичне оцінювання № 5 Мета уроку: перевірити навчальні досягнення учнів з теми “Декартові координати у просторі”. Хід уроку Тематичне оцінювання № 5 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 5 Варіант А 1. Чи лежать точки А, В, С на одній прямій, якщо А(1;1;-3), В (-1;3;5), С […]...

  3. Прямокутна система координат на площині УРОК № 22 Тема. Прямокутна система координат на площині Мета уроку: узагальнення та систематизація матеріалу про декартову прямокутну систему координат. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують прямокутну систему координат. Застосовують вивчені означення до розв’язування задач. Хід уроку I. Перевірка домашнього завдання […]...

  4. ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 19. ГЕОМЕТРИЧНЕ МІСЦЕ ТОЧОК Щоб розв’язувати складніші задачі на побудову, потрібно знати, що таке геометричне місце точок. Геометричним місцем точок (ГМТ) називають фігуру, яка складається з усіх точок, що мають певну властивість. Розглянемо кілька геометричних місць точок площини. Коло – геометричне місце точок, рівновіддалених від даної точки. […]...

  5. Перпендикулярні та паралельні прямі. Координатна площина Урок № 119 Тема. Перпендикулярні та паралельні прямі. Координатна площина Мета: перевірити й оцінити рівень знань та вироблених умінь і навичок, які є обов’язковими для опанування теми. Тип уроку: контроль і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Збираємо зошити з домашньою контрольною роботою для перевірки. III. Умова […]...

  6. Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...

  7. Відстань між двома точками із заданими координатами УРОК № 24 Тема. Відстань між двома точками із заданими координатами Мета уроку: виведення формули для знаходження відстані між двома точками, заданими координатами, і застосування формул до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і доводять формулу для знаходження відстані […]...

  8. Відрізки Урок № 4 Тема. Відрізки Мета: домогтися засвоєння учнями: – змiсту аксiоми вiдкладання вiдрiзкiв та сфери її застосування; – мiсту поняття вiдстанi мiж двома точками та властивостей рiвних вiдрiзкiв i властивостей порiвняння вiдрiзкiв. Сформувати вмiння: – вiдтворювати аксiому вiдкладання вiдрiзкiв; – застосовувати названу аксiому для розв’язування вiдповiдних задач; – застосовувати властивостi порiвняння вiдрiзкiв разом iз […]...

  9. Координатна площина Урок № 113 Тема. Координатна площина Мета: відпрацювати навички “читати” готові рисунки з точкам на координатній площині та будувати точки із заданими координатами; здійснити діагностику знань і вмінь з теми. Тип уроку: застосування знань, умінь, навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання @ Бажано звернути увагу на задачу 4 – повторити спосіб […]...

  10. Тематичне оцінювання № 1 Урок 12 Тема. Тематичне оцінювання № 1 Мета уроку: перевірка навчальних досягнень учнів з тем “Вступ до стереометрії” та “Взаємне розміщення прямих у просторі”. Хід уроку Тематичне оцінювання № 1 можна провести, враховуючи результати ви­конання самостійної роботи на уроці № 6 та результати контрольної роботи. 1. Тематична контрольна робота № 1 Варіант А Варіант 1 […]...

  11. Відстань між двома точками простору Урок 45 Тема. Відстань між двома точками простору Мета уроку: виведення формул для знаходження відстані між двома точками, заданих координатами, та застосування формули до розв’язування задач. Обладнання: схема “Відстань між двома точками”, модель куба. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Ребро куба дорівнює 10: варіант 1 […]...

  12. Промiнь (пiвпряма) Урок № 2 Тема. Промiнь (пiвпряма) Мета: домогтися засвоєння учнями означення променя, доповняльних пiвпрямих та поняття “означення деякого об’єкта”; домогтися оволодiння учнями вмiнням позначати й розрiзняти на рисунку променi, доповняльнi променi, виконувати рисунок за описом ситуацiї з використанням вивченої термiнологiї. Тип уроку: засвоєння знань, умiнь та навичок. Форма проведення: фронтальна бесiда. Наочнiсть та обладнання: таблиця […]...

  13. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  14. Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  15. Вступ. Точка і пряма. Властивості точок і прямих Урок № 1 Тема. Вступ. Точка і пряма. Властивості точок і прямих Мета: ознайомити учнiв з предметом вивчення геометрiї, планiметрiї та iз поняттям найпростiших фiгур у геометрiї, домагатися вiд учнів свiдомого засвоєння термiнологiї, що описує взаємне розташування точок та прямих на площинi, формулювання основних властивостей розташування точок та прямих; виробити первиннi вмiння позначати точки та […]...

  16. Паралельне перенесення УРОК № 37 Тема. Паралельне перенесення Мета уроку: формування поняття паралельного перенесення та вивчення властивостей паралельного перенесення; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують паралельне перенесення; будують фігури, у які переходять дані фігури при паралельному […]...

  17. ОЗНАЙОМЛЕННЯ З НАЗВАМИ ГЕОМЕТРИЧНИХ ТІЛ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ З НАЗВАМИ ГЕОМЕТРИЧНИХ ТІЛ; ЗАКРІПЛЮВАТИ ВМІННЯ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА РУХ; РОЗВИВАТИ ОБЧИСЛЮВАЛЬНІ НАВИЧКИ I. Перевірка домашнього завдання Фронтально з’ясувати, за якими правилами обчислили невідомі величини у вправі 518. У задачі 519 пояснити вибір дій. II. Актуалізація та корекція опорних знань учнів 1. Завдання для опитування. 1) За таблицею знайти невідомі значення […]...

  18. Властивість точки, рівновіддаленої від сторін многокутника Урок 36 Тема. Властивість точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, вписане в многокутник” Хід уроку 1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку. Нехай ABCD […]...

  19. Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...

  20. Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...

  21. Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...

  22. Розв’язування задач на застосування властивості точки, рівновіддаленої від сторін многокутника Урок 37 Тема. Розв’язування задач на застосування властивості точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір. Хід уроку 1. Два учні відтворюють розв’язування задач № 46, 47, а в цей час клас пише математичний диктант. 2. Математичний диктант. З центра […]...

  23. Паралельне перенесення в просторі Урок 49 Тема. Паралельне перенесення в просторі Мета уроку: формування знань учнів про паралельне перенесення в просторі; вивчення його властивостей та застосування їх до розв’язування задач. Обладнання: схеми “Відстань між двома точками” (див. урок 46) і “Координати середини відрізка” (див. урок 47), моделі куба і прямокутного паралелепіпеда. Хід уроку І. Перевірка домашнього завдання 1. Перевірити […]...

  24. Паралельні прямі. Властивості паралельних прямих Урок № 110 Тема. Паралельні прямі. Властивості паралельних прямих Мета: закріпити знання учнів про властивості паралельних прямих; відпрацювати навички розв’язування задач, що передбачають застосування набутих з теми знань; продовжувати роботу з повторення вивченого у 6 класі матеріалу. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Математичний диктант […]...

  25. Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530) Тема. Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530). Мета. Узагальнити зв’язки між відстанню, часом і швидкістю; закріплювати вміння учнів розв’язувати задачі на обчислення згаданих величин, виконувати дії над іменованими числами; ознайомити з назвами геометричних тіл. Обладнання. Таблиця усних обчислень; […]...

  26. Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...

  27. Побудова перерізів многогранників Урок 20 Тема. Побудова перерізів многогранників Мета уроку: формування вмінь учнів застосовувати властивості паралельних площин до розв’язування вправ, побудови перерізів. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Три учні відтворюють розв’язування задач № 28, 30, 31 на дошці, в цей час клас пише математичний диктант. 2. Математичний диктант. Через вершини А, В, […]...

  28. Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...

  29. ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ФІГУР БУКВАМИ ЛАТИНСЬКОГО АЛФАВІТУ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ Урок 18. ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ФІГУР БУКВАМИ ЛАТИНСЬКОГО АЛФАВІТУ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. (Розглядання двох задач, які мають спільну частину умови) Мета: вчити учнів позначати геометричні фігури буквами латинського алфавіту; розглянути і порівняти задачі, які мають спільну частину умови; […]...

  30. Існування площини, яка проходить через три дані точки УРОК 4 Тема. Існування площини, яка проходить через три дані точки Мета уроку: вивчення теореми про існування єдиної площини, яка проходить через три дані точки, які не лежать на одній прямій. Обладнання: стереометричний набір, моделі куба і тетраедра. Хід уроку 1. Один із учнів відтворює розв’язування задачі № 10, решта класу пише математичний диктант. 2. […]...

  31. Перетворення подібності та його властивості. Гомотетія УРОК № 38 Тема. Перетворення подібності та його властивості. Гомотетія Мета уроку: формування понять перетворення подібності й гомотетії; вивчення властивостей перетворення подібності; формування вмінь застосовувати вивчені властивості й означення до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення подібності” [13]. Вимоги до рівня підготовки учнів: описують перетворення подібності й гомотетію; будують фігури, у […]...

  32. Геометричне місце точок Урок № 47 Тема. Геометричне місце точок Мета: – сформувати в учнів уявлення про зміст поняття “геометричне місце точок”, властивість і ознаку точок, що належать ГМТ ; – сформувати знання змісту та схеми доведення теореми про ГМТ. Сформувати вміння: – відтворювати означення властивості та ознаки ГМТ, теорем про ГМТ; – використовувати ці твердження під час […]...

  33. СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА МАЛЮНКОМ І СХЕМОЮ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 55. СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА МАЛЮНКОМ І СХЕМОЮ. ДОПОВНЕННЯ РІВНОСТЕЙ І НЕРІВНОСТЕЙ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР Мета: навчати учнів складати і розв’язувати задачі на збільшення і зменшення числа на кілька одиниць за малюнком і схемою; закріплювати вміння доповнювати рівності і нерівності, розпізнавати геометричні фігури; вдосконалювати обчислювальні […]...

  34. Норматив робочих місць для працевлаштування інвалідів Норматив робочих місць для працевлаштування інвалідів – передбачена законодавством кількість робочих місць для працевлаштування інвалідів. Н. р. м. в Україні становить не менше 4 відсотків від загального числа працюючих; якщо працює від 15 до 20 громадян – встановлюється норматив у кількості одного робочого місця. Підприємства, установи, організації, що не забезпечують виконання Н. р. м. для […]...

  35. Перетин прямої з площиною. Перерізи многогранників УРОК 3 Тема. Перетин прямої з площиною. Перерізи многогранників Мета уроку: ознайомлення учнів із взаємним розташуванням прямої і площини у просторі. Вивчення теореми про належність прямої до площини. Формування поняття перерізу многогранника. Обладнання: моделі многогранників, схема “Взаємне розташування прямої і площини”, стереометричний набір. 1. Фронтальне опитування. 1) Скільки площин визначають дві прямі, які перетинаються? 2) […]...

  36. Координатна площина. Графіки залежності Урок № 117 Тема. Координатна площина. Графіки залежності Мета: вдосконалити вміння учнів, вироблені в ході вивчення теми шляхом розв’язування задач підвищеної складності; відпрацьовувати обчислювальні навички. Тип уроку: застосування знань, умінь та навичок. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Під час аналізу виконання задачі 1 звертаємо увагу на те, що для відповіді на […]...

  37. Паралельне проектування та його властивості. Зображення просторових фігур на площині Урок 21 Тема. Паралельне проектування та його властивості. Зображення просторових фігур на площині Мета уроку: формування знань про паралельне проектування. Вивчення властивостей паралельного проектування. Дати уявлення про зображення просторових фігур на площині. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Відповісти на запитання, які виникли в учнів при розв’язуванні до­машньої задачі. 2. Самостійна […]...

  38. Розв’язування вправ. Самостійна робота УРОК 4 Тема. Розв’язування вправ. Самостійна робота Мета уроку: формування умінь будувати графіки функцій за до­помогою геометричних перетворень. І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування вправи № 3 (4; 5; 6), дру­гий – № 3 (7; 8; 9), третій – № 3 (18). 2. Математичний диктант. Запишіть формулою функцію, графік якої одержано в […]...

  39. Найпростіші геометричні фігури та їх властивості Урок № 14 Тема. Найпростіші геометричні фігури та їх властивості Мета: перевірити та оцінити рівень засвоєння знань та вмінь учнів з теми, передбачених програмою; виявити прогалини в знаннях та вміннях учнів для подальшого їх усунення. Тип уроку: перевірка та корекція знань, навичок та вмінь. ХІД УРОКУ І. Умова тематичної контрольної роботи Варіант 1 Початковий рівень […]...

  40. Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...

Ви зараз читаєте: Метод геометричних місць
«
»