МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ
“МЕХАНІЧНІ КОЛИВАННЯ І ХВИЛІ”
Заліковий урок-гра “Краф”
Мета. Навчити учнів розв’язувати задачі різного типу за допомогою групової форми роботи; виховувати толерантність та вміння співпрацювати.
Тип уроку. Урок контролю та корекції знань.
Методичні поради. Одним із найважливіших завдань учителя фізики є навчити учнів розв’язувати задачі різного типу складності. Проте проконтролювати якість уміння розв’язувати задачі інколи доволі складно. У такому разі в пригоді можуть стати нетрадиційні форми і методи
Якщо клас не ознайомлений із груповою формою роботи, то за кілька уроків до проведення гри його слід
Гра складається з чотирьох етапів, кожний із яких розрахований не менш як на 10 хв., тому оптимальним варіантом було б проведення її протягом спареного уроку. Напередодні проведення гри вчитель готує інформаційний лист, на якому написані прізвища учнів класу, є 7 вертикальних колонок, кожна з яких позначена вгорі відповідним номером: 1 – подача розв’язку; 2 – захист задачі; 3 – правильність розв’язання; 4 – рецензія задачі; 5 – власна задача; 6 – сума балів; 7 – оцінка за дванадцятибальною шкалою. Під час проведення гри асистент (лаборант) допомагає вчителеві вести калькуляцію балів і наклеювати папірці з позначенням кількості балів на інформаційний лист.
Хід уроку
I етап
Гра починається із жеребкування між керівниками груп для визначення номера кожної групи. Отримавши пакети завдань (відповідно до номера групи), керівники приєднуються до учнів своєї групи і починають розв’язувати задачі. Кожний пакет містить 4 задачі, дві з яких розв’язують керівники груп (вони позначені зеленими кружечками), а інші дві (вони позначені червоними кружечками) – інші члени груп. На розв’язування всіх завдань відводиться 10 хв. Протягом цього часу кожен учень (в середньому) має розв’язати одну задачу і записати розв’язання на аркуші паперу під копіювальний папір. (Орієнтовні задачі додаються). Завірену підписом керівника групи (що свідчить про згоду останнього з розв’язанням) копію оформленої задачі учні здають учителеві й отримують свої 5 балів. Учні, які не вклалися у 10 хв., втрачають по одному балу за кожну прострочену хвилину. Учитель звіряє розв’язання зі своїм і оцінює його за п’ятибальною шкалою, проте оцінка на цьому етапі на інформаційний лист не заноситься. Під час виконання завдання в класі може звучати тиха, спокійна музика. На цьому перший етап гри “КРАФ” завершується.
II етап
Після подання учнем розв’язання задачі він готується біля дошки до його захисту перед керівниками інших груп. Головним рецензентом розв’язання в цьому разі є керівник тієї групи, що розв’язувала дві такі ж задачі, але у якої вони були контрольні й позначені червоним, а не зеленим кольором. (Для того щоб кожен рецензент міг заздалегідь знати, захист якої групи він має слухати, номер рецензованої групи можна позначити в дужках безпосередньо на пакеті завдань, які отримують на початку гри керівники груп; в такому разі позначення 4 (5) означатиме: група № 4 рецензує групу № 5. (Див. також: табл. 1.)) Таким чином, будь-які дві задачі, позначені для однієї групи зеленим кольором, є контрольними для іншої групи. Кожна задача, що розв’язується одним членом групи, може бути перевірена керівником іншої групи. За захист задачі учень може отримати до 10 балів, а керівник групи, до якої він належить, – до 5 балів. Таким чином, кожний керівник групи на цьому етапі може отримати 10 балів лише в тому разі, якщо два члени його групи захистяться без втрати балів. Рецензент, звіряючи власне розв’язання з поданим, оцінює його. За вдалу рецензію учень (керівник групи) може отримати від 2 до 7 балів. Керівники інших груп і решта учнів класу, які до цього часу впоралися зі своїми задачами (а таких гіпотетично має бути переважна більшість), також слухають запропоноване розв’язання задачі і, за бажання, можуть висловити свою думку, внести корективи чи доповнення. Захист задачі разом із рецензією триває до 5 хв. Учням, які не братимуть участі у захисті, і, таким чином, не зможуть набрати собі в такий спосіб бали, пропонується працювати над розв’язком двох додаткових задач і подати їх у кінці уроку на оцінку вчителю. Після того як розв’язання задачі захистив кожний бажаючий, другий етап гри “КРАФ” завершується
III етап
Квінтесенцією гри є складання учнями умови власної задачі за даною темою для розв’язування її іншими учнями класу. За вдало запропоновану задачу відповідного ступеня складності учень отримує до 20 балів.
IV етап
Підбивання підсумків уроку і виставлення оцінок. Відповідно до кількості набраних балів учням виставляються оцінки (табл. 2).
Учень, який набрав найбільшу кількість балів, отримує звання “КРАФ” – кращий фізик класу – і заохочується (стає, наприклад, керівником групи).
Додатки
Таблиця 1
Розподіл задач між групами і схема рецензування відповідей керівниками груп
Номер групи (номер групи, що рецензується) | Задачі для рядових членів групи (позначені червоним кольором) | Задачі для керівників груп (позначені зеленим кольором) |
І (II) | 1,4 | 7,10 |
П (III) | 7,10 | 8,11 |
III (IV) | 8,11 | 3,6 |
IV (V) | 3,6 | 9,12 |
V(VI) | 9,12 | 2,5 |
VI (І) | 2,5 | 1,4 |
Таблиця 2
Оцінювання учасників гри “КРАФ”
Оцінка | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Бали | 0-2 | 3-4 | 5-6 | 7-10 | 11-14 | 15-18 | 19-21 | 22-24 | 25-27 | 28-30 | 31-33 | 34-36 |
Орієнтовні задачі для проведення заліку у формі гри “КРАФ” за темою “Механічні коливання і хвилі”
1. Годинник, період коливання маятника якого дорівнює 1 с (годинник із секундним маятником), на поверхні Землі йде точно. Наскільки відставатиме годинник за добу, якщо його підняти на висоту 200 м над поверхнею Землі!
Розв’язання. Нехай t1 i t2 – покази годинника на висоті h = 200 м і на поверхні Землі відповідно. Тоді відставання годинника за добу становитиме? t = t2 – t1 (1). Зрозуміло, що покази годинника пропорційні до кількості коливань його маятника t2/t1 = N2/N1. Звідки: 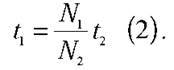 У свою чергу, кількості коливань маятника N1 i N2 пов’язані з його періодами коливань на висоті h і на поверхні Землі відповідно:
У свою чергу, кількості коливань маятника N1 i N2 пов’язані з його періодами коливань на висоті h і на поверхні Землі відповідно: 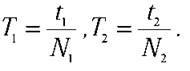
З останніх формул маємо: 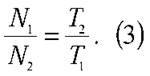
З іншого боку, 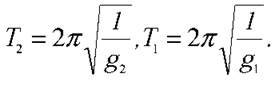
Тому 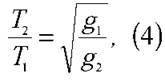 де g1 i g2 – прискорення вільного падіння на висоті h і на поверхні Землі відповідно.
де g1 i g2 – прискорення вільного падіння на висоті h і на поверхні Землі відповідно.
Відомо, що 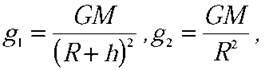 Де R – радіус Землі. Тоді
Де R – радіус Землі. Тоді 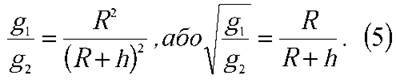
З формул (5) і (4) маємо: 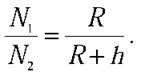
Останній вираз підставимо у (2): 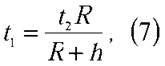 і, нарешті, з формул (7) і (1) маємо розрахункову формулу:
і, нарешті, з формул (7) і (1) маємо розрахункову формулу: 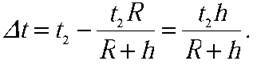
Перевіримо найменування: 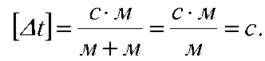
Підставимо числові значення і отримаємо відповідь: ?t = 2,71 c.
2. З яким прискоренням a і в якому напрямі має рухатися кабіна ліфта, щоб секундний маятник, який знаходиться в ній, за час t = 2 хв. 20 с зробив N = 100 коливань.
Розв’язання. Оскільки маятник перебуває в неінерційній системі відліку, то період його коливань можна визначити за формулою 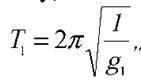 Де g1 – прискорення вільного падіння в неінерційній системі відліку, g1 = g ± a (знак “+” відповідає рівноприскореному рухові ліфта вгору; а знак “-” – униз). Звідси: a = g1 – g (1) (знак прискорення вкаже на напрям руху ліфта).
Де g1 – прискорення вільного падіння в неінерційній системі відліку, g1 = g ± a (знак “+” відповідає рівноприскореному рухові ліфта вгору; а знак “-” – униз). Звідси: a = g1 – g (1) (знак прискорення вкаже на напрям руху ліфта).
Оскільки маятник секундний (T = 1c), то його період коливань у ліфті, що рухається без прискорення (чи зберігає стан спокою), обчислюється за формулою 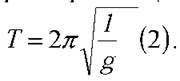 Звідси можна знайти його довжину:
Звідси можна знайти його довжину: 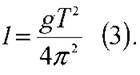
Період коливання маятника в неінерційній системі відліку можна обчислити, з одного боку, за формулою 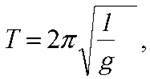 а з іншого – за формулою T1 = t/N. Отже, маємо:
а з іншого – за формулою T1 = t/N. Отже, маємо: 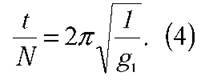
Підставивши (3) в (4), знайдемо, що 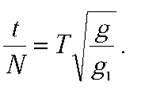
Звідси: 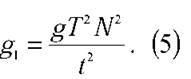
Останню формулу підставимо в (1): 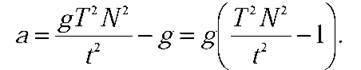
Перевіримо найменування: 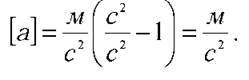
Підставивши числові значення величин, отримаємо: a? -4,8 м/c2.
Знак “мінус” показує, що ліфт рухався з прискоренням, напрямленим вниз.
3. На скільки відсотків потрібно змінити довжину математичного маятника, що знаходиться у вагоні, який рухається горизонтально з прискоренням a1 = 2,4 м/c2, щоб період його коливань дорівнював періоду коливань маятника, який рухається в кабіні ліфта вгору з прискоренням a = 4,2 м/c2?
Розв’язання. Нехай l, l1 – довжини маятників, що знаходяться у кабіні ліфта і вагоні відповідно. Тоді період коливань першого маятника визначається за формулою 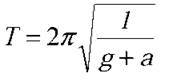 (див. задачу № 2). Другий маятник знаходитиметься в неінерційній системі відліку, в якій прискорення вільного падіння
(див. задачу № 2). Другий маятник знаходитиметься в неінерційній системі відліку, в якій прискорення вільного падіння 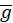 1 дорівнює сумі векторів
1 дорівнює сумі векторів 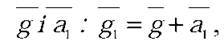 а модуль
а модуль 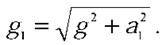 Отже, період коливань цього маятника
Отже, період коливань цього маятника 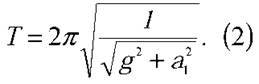
За умовою задачі періоди обох маятників однакові, тому 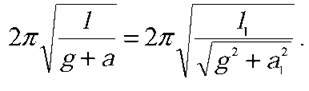
Після перетворень знаходимо: 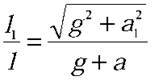
Шукану зміну довжини (у відсотках) визначимо за формулою 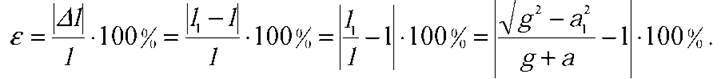
Після підстановки числових значень отримаємо: ? ? 28%..
4. Тіло, маса якого дорівнює 200 г, коливається за законом 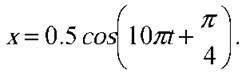 Знайти залежність сили, що діє на тіло, від часу. Чому дорівнює найбільше значення модуля сили? В які моменти модуль сили набуває найбільшого і найменшого значень?
Знайти залежність сили, що діє на тіло, від часу. Чому дорівнює найбільше значення модуля сили? В які моменти модуль сили набуває найбільшого і найменшого значень?
Розв’язання. За другим законом Ньютона: F = ma, де 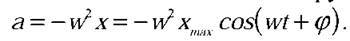 Отже,
Отже, 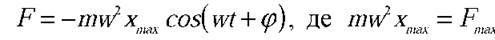 – найбільше значення сили, а w = 10
– найбільше значення сили, а w = 10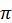 .
.
Найбільше значення модуль періодично діючої сили набуває в ті моменти часу, коли фаза її коливань дорівнює 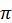 N.
N.
Отже, 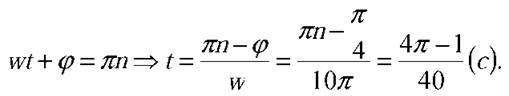
Найменшого значення модуля сила набуває в ті моменти часу, коли фаза її коливань дорівнює 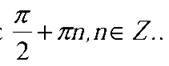 Отже, маємо:
Отже, маємо: 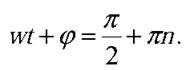
Звідси 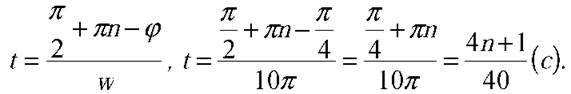
Підставляючи числові значення, отримаємо відповідь:
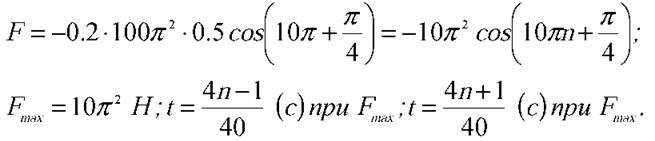
5. Амплітуда коливань математичного маятника дорівнює 5 мм, а довжина – 1 м. Як залежить зміщення кульки маятника від часу? За початок відліку прийняти: а) момент проходження нижнього положення зліва направо; б) момент проходження крайнього правого положення. Зміщення кульки вважатимемо додатним тоді, коли вона відхиляється вправо, коли ж кулька відхиляється вліво, зміщення вважатимемо від’ємним. Знайти максимальне значення модуля сили, що діє на маятник, якщо його маса дорівнює 40 г.
Розв’язання. Математичний маятник здійснює гармонічні коливання, тому зміщення кульки з часом відбуватиметься за законом синуса або косинуса, залежно від того, момент якого положення маятника прийняти за початок відліку часу. Для запису аналітичного виразу залежності x = x(f) потрібно знати циклічну частоту коливань маятника. Відомо, що
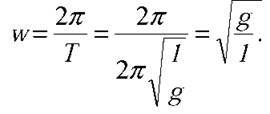
Якщо за початок відліку прийняти момент проходження кулькою нижнього положення (пункт а) умови задачі), то це означає, що коливання відбуваються за законом синуса: 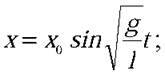 якщо ж за початок відліку прийняти момент проходження кулькою крайнього правого положення (пункт б) умови задачі), то коливання відбуваються за законом косинуса:
якщо ж за початок відліку прийняти момент проходження кулькою крайнього правого положення (пункт б) умови задачі), то коливання відбуваються за законом косинуса: 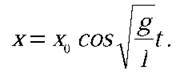
Максимальне значення модуля сили, що діє на кульку, обчислимо за формулою: 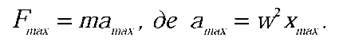
Тоді маємо: 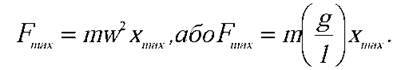
Перевіримо найменування: 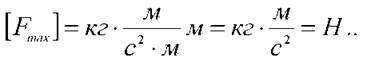
Підставляючи числові значення у розрахункові формули, отримуємо: 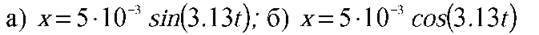
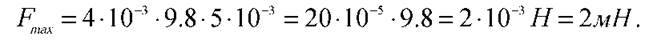
6. Циклічна частота вільних коливань осцилятора дорівнює w. Протягом якого найменшого часу максимальна кінетична енергія осцилятора зменшиться удвічі?
Розв’язання. Кінетична енергія осцилятора періодично змінюється з часом відповідно до швидкості тіла, що коливається. Нехай зміна швидкості з часом відбувається за законом косинуса: v = v0 cos wt. Тоді миттєве значення кінетичної енергії можна знайти за формулою 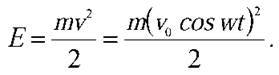 За умовою задачі кінетична енергія осцилятора протягом деякого шуканого часу t зменшилася вдвічі:
За умовою задачі кінетична енергія осцилятора протягом деякого шуканого часу t зменшилася вдвічі: 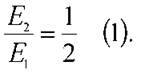
Але 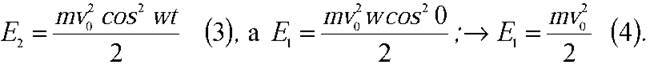
Підставляючи (3) і (4) в (1), маємо: 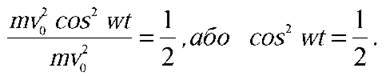
Звідси 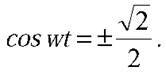 Найменше додатне значення аргументу, за якого косинус кута набуває таких значень, становить
Найменше додатне значення аргументу, за якого косинус кута набуває таких значень, становить 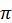 /4. Отже, wt =
/4. Отже, wt = 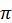 /4, звідси t =
/4, звідси t = 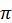 /4w.
/4w.
7. За якої швидкості потяга ресори вагонів найсильніше коливатимуться під дією поштовхів коліс на стиках рейок? Довжина рейок дорівнює l, навантаження на ресори – F, ресора прогинається на h за навантаження F1.
Розв’язання. Ресори коливатимуться найсильніше за умови виникнення резонансу, тобто тоді, коли період Т власних коливань ресор збігається з періодом 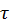 зовнішньої сили (з інтервалом часу між двома послідовними поштовхами на стиках рейок). Отже, T =
зовнішньої сили (з інтервалом часу між двома послідовними поштовхами на стиках рейок). Отже, T = 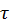 (1). Період власних коливань ресори
(1). Період власних коливань ресори 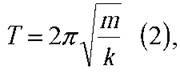 де k – її жорсткість, m – маса вантажу, яка спричиняє силу F.
де k – її жорсткість, m – маса вантажу, яка спричиняє силу F.
Оскільки F = mg, то m = F/g (3). Жорсткість ресор можна знайти із формули k = F1/h (4). Підставивши (3) і (4) у (2), маємо 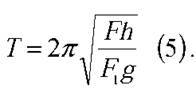 Оскільки рух потяга рівномірний, а довжина рейок дорівнює l, можна визначити час між двома послідовними поштовхами на стиках рейок:
Оскільки рух потяга рівномірний, а довжина рейок дорівнює l, можна визначити час між двома послідовними поштовхами на стиках рейок: 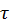 = 1/v (6). Підставимо (5) і (6) у (1):
= 1/v (6). Підставимо (5) і (6) у (1): 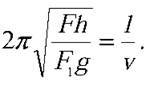 Звідки
Звідки
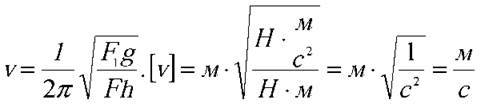
8. У вагоні потяга, який рухається зі швидкістю 67,5 км/год., висить маятник. Визначити довжину маятника, за якої він розгойдуватиметься найсильніше, якщо довжина рейок дорівнює 25 м. Скільки коливань здійснить такий маятник, коли потяг проїде 20 км?
Розв’язання. Під час удару коліс об стики рейок вагон отримує імпульс, що має вертикальну і горизонтальну складові. Маятник розгойдуватиметься найсильніше, якщо період його власних коливань збігатиметься з інтервалом часу проходження коліс вагона між двома послідовними стиками рейок: T = 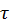 (1). Період коливань математичного маятника завдовжки l визначається за формулою:
(1). Період коливань математичного маятника завдовжки l визначається за формулою: 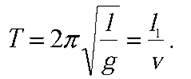
Звідси: 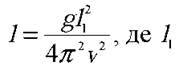 – довжина рейки.
– довжина рейки.
Для визначення кількості коливань N маятника скористаємося формулою N = vt (2), де t – час, протягом якого здійснювалися коливання, v – частота коливань маятника. Оскільки 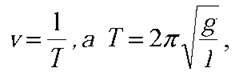 маємо:
маємо: 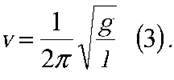 З кінематики відомо, що t = s/v (4). Формули (3) і (4) підставимо у формулу (2):
З кінематики відомо, що t = s/v (4). Формули (3) і (4) підставимо у формулу (2): 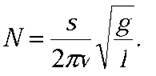
Перевіримо найменування: 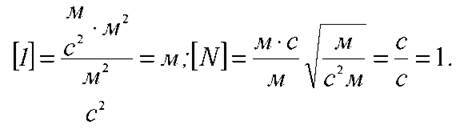
Підставивши числові значення, знайдемо l = 44 см, N = 801.
9. Хвилі поширюються зі швидкістю 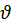 = 360 м/c за частоти v = 450 Гц. Чому дорівнює різниця фаз коливань двох точок, віддалених одна від одної на 20 см уздовж: хвильового променя? На скільки відсотків слід змінити період коливань джерела хвиль, щоб за тій ж різниці фаз відстань між ними зросла на 10 см?
= 360 м/c за частоти v = 450 Гц. Чому дорівнює різниця фаз коливань двох точок, віддалених одна від одної на 20 см уздовж: хвильового променя? На скільки відсотків слід змінити період коливань джерела хвиль, щоб за тій ж різниці фаз відстань між ними зросла на 10 см?
Розв’язання. Запишемо рівняння хвилі: 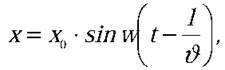 де x зміщення частинки, що перебуває на відстані l від джерела хвиль. Тоді кінематичні рівняння коливання частинок, розташованих від джерела на відстанях l1 і l2 (l1 > l2) матимуть вигляд:
де x зміщення частинки, що перебуває на відстані l від джерела хвиль. Тоді кінематичні рівняння коливання частинок, розташованих від джерела на відстанях l1 і l2 (l1 > l2) матимуть вигляд: 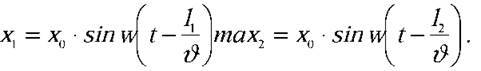 Звідси різниця фаз коливань частинок:
Звідси різниця фаз коливань частинок:
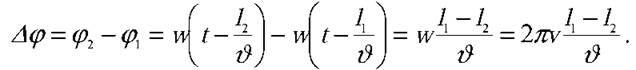
Для того, щоб відповісти на друге запитання задачі, перепишемо останню формулу так, щоб різниця фаз виражалася через період коливань джерела хвиль: 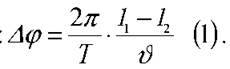 Згідно з умовою задачі, за умови зміни періоду коливань (від деякого значення T1, до деякого значення T2) відстань між точками, що коливаються з певною різницею фаз, має збільшитися на l = 10 см.
Згідно з умовою задачі, за умови зміни періоду коливань (від деякого значення T1, до деякого значення T2) відстань між точками, що коливаються з певною різницею фаз, має збільшитися на l = 10 см.
Отже, можна записати:
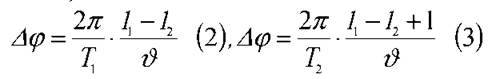
Звідси: 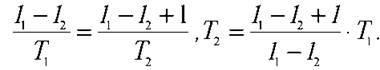
Знайдемо відносну зміну періоду коливань:
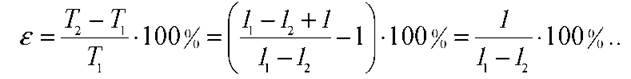
Після обчислень маємо: 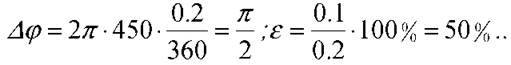
10. Швидкість поширення звуку у воді дорівнює 1450 м/с. На якій відстані перебувають найближчі точки, що здійснюють коливання у протифазі, якщо частота коливань становить 725 Гц?
Розв’язання. Скористаємося виведеною в попередній задачі формулою залежності різниці фаз коливань двох точок від відстані між ними: 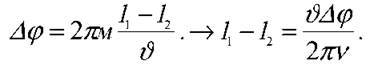
За умовою задачі коливання відбуваються у протифазі, тобто?? = 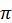 . Після обчислень маємо:
. Після обчислень маємо:
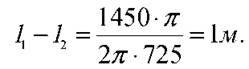
11. Визначити потенціальну енергію U математичного маятника масою m = 20 г у положенні, що відповідає куту відхилення нитки від вертикалі? = 100, якщо частота коливань маятника v = 0,5 c-1. Потенціальну енергію маятника в положенні рівноваги вважати такою, що дорівнює нулеві. Записати рівняння залежності зміщення від часу; якщо за початок відліку прийнято момент проходження крайнього правого положення, а амплітуда коливань становить 20 см.
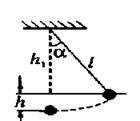
Мал. 1.
Розв’язання. Потенціальна енергія маятника дорівнює U = mgh, де h – висота, на яку піднялося тіло. Якщо довжина нитки дорівнює l, то h = l – h1 (див. мал. 1).
Оскільки 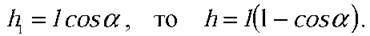 Довжину маятника визначимо з формули для періоду коливань
Довжину маятника визначимо з формули для періоду коливань 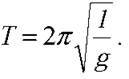
Врахувавши, що T = 1/v, маємо: 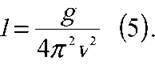
Тоді 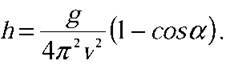
Тепер можна знайти потенціальну енергію маятника: 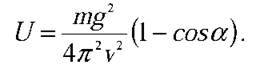
Перевіримо найменування: 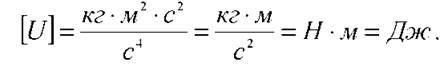
Після обчислень маємо, що U = 2,96 мДж. Проводячи міркування, аналогічні тим, що наведені у розв’язанні задачі № 6, можна записати: x = 0,2 cos(2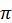 – 0,5t) = 0,2 cos
– 0,5t) = 0,2 cos 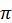 T.
T.
12. На шальку, підвішену на пружині жорсткості k, падає кулька масою m і залишається на шальці. Амплітуда коливань, які почала здійснювати пружина після падіння кульки, становить х0. Визначити, з якої висоти впала кулька, якщо масами шальки і пружини можна знехтувати.
Розв’язання. Нехай h – висота, з якої впала кулька, x – віддаль від положення рівноваги (рівень В), навколо якого відбуваються коливання до нижнього кінця пружини (рівень С) у момент падіння кульки, х0 – амплітуда коливань (див. мал. 2). У момент падіння кульки на шальку швидкість кульки дорівнює 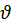 = 2gh. Після зіткнення з шалькою ця швидкість не змінилася. Це є наслідком закону збереження імпульсу і того, що маса шальки дорівнює нулю. Отже, втрат енергії системи не відбувається. Тому запишемо закон збереження енергії системи, беручи до уваги початковий момент (кулька перебуває на висоті А) і момент нижнього положення кульки.
= 2gh. Після зіткнення з шалькою ця швидкість не змінилася. Це є наслідком закону збереження імпульсу і того, що маса шальки дорівнює нулю. Отже, втрат енергії системи не відбувається. Тому запишемо закон збереження енергії системи, беручи до уваги початковий момент (кулька перебуває на висоті А) і момент нижнього положення кульки.
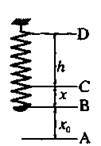
Мал. 2.
За нуль потенціальної енергії виберемо рівень А. Тоді: 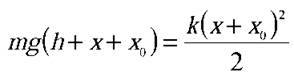 , де kx = mg. Звідки
, де kx = mg. Звідки