Многогранники
663.
А)
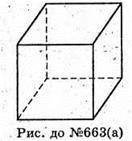
Грань – Г = 6; ребро – Р = 12; вершина – В = 8.
Теорема Ейлера:
В – Р + Г; 8 – 12 + 6 = 2.
Б)
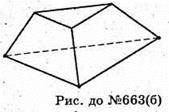
Г = 5;
Р = 9;
В = 6.
6 – 9 + 5 = 2
В)
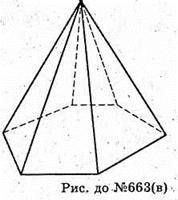
Г= 7;
Р = 12;
В = 7.
7 – 12 + 7 = 2.
Г)
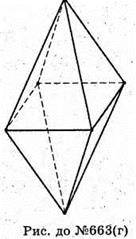
Р = 8;
Р = 12;
В = 6.
6 – 12 + 8 = 2.
664.
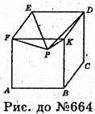
Многогранник неопуклий, а грані – опуклі многокутники:
Квадрати і трикутники: ΔFEP; ΔEPD; ΔDPK; ΔFPK.
665.
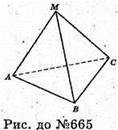
Многогранник
Тетраедр МАВС.
666.
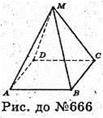
Многогранник має 5 граней і 5 вершин.
8 ребер має такий многогранник.
667.
Такий многогранник має 9 ребер.
668.
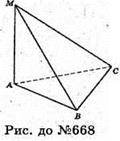
Такий многогранник існує.
Цей многогранник не є тетраедром.
669.
Нехай дано опуклий многогранник, в основі якого лежить многокутник.
Цей многокутник можна розбити на скінченну кількість трикутників, які будуть основами скінченної кількості трикутних пірамід. Отже, довільний опуклий многогранник можна розбити на скінченну кількість трикутних
670.
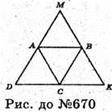
Розгортка правильного тетраедра, довжина ребра якого 2 см,
Складається з чотирьох правильних трикутників.
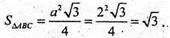
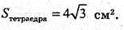
Відповідь: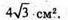 
671.
Площа поверхні правильного тетраедра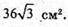 
Площа одного трикутника: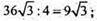 
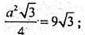а2 =36; а = 6 см.
Відповідь: 6 см.
672.
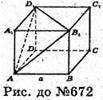
Від куба A1B1С1D1АBCD відрізали тетраедр A1AB1D1, залишився многогранник ABCDD1B1C1.
Граней: 7.
Ребер: 12.
Вершин: 7.
Найбільша грань має площу а2.
673.
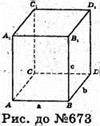
Нехай дано паралелепіпед із вимірами АВ = а, ВС = b, AB = с, тоді за умовою: ab = 2 м2; bс = 3 м2; ас = 4 м2;
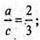
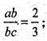
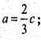
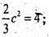2с2 = 12 ; с2 = 6;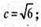 
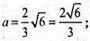
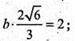
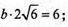
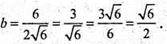
S поверхні = 2ab + 2bc + 2ac;
S поверхні = 2 × 2 + 2 × 3 + 2 × 4 = 4 + 6 + 8= 18 (м2).
Відповідь; 18 м2.
674.
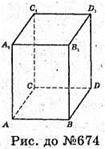
Нехай дано прямокутний паралелепіпед, довжина одного ребра АВ = a,
Sαα1ββ1 = S1, SABCD = S2.
Площа поверхні: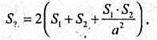 
Відповідь: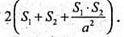 
675.
А)
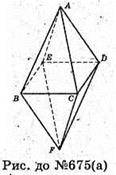
Гранями опуклого многогранника є тільки трикутники.
У нього 12 ребер, 6 вершин, 8 граней;
Б)
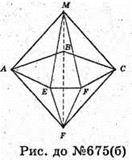
Опуклий многогранник, гранями якого є тільки трикутники.
У нього 15 ребер, 7 вершин, 10 граней.
676.
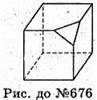
Для цього многогранника не виконується теорема Ейлера. Граней – 7.
677.
Якщо в основі піраміди опуклий многокутник, то її можна розбити на скінченну множину опуклих трикутників, із яких одержимо піраміди, основами яких будуть опуклі трикутники. Отже така піраміда є опуклий многогранник.
678.
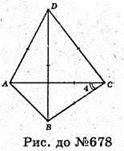
Нехай дано тетраедр ABCD, AD = BD = DC = ВС = АС = a, ∠ACB = φ.
α = 1,2 м, φ = 50°.
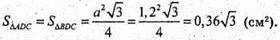
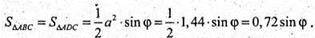
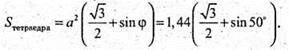
679.
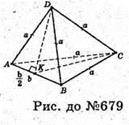
Нехай дано тетраедр ABCD, AD = BD = DC = BC = AC = a, AB = b.
ΔAKD – прямокутний. DK2 = AD2 – AK2;
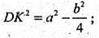
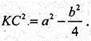Отже, DK = KC.
ΔADC = ΔDBC – рівносторонні. ΔADB – рівнобедрений.
AD + DB > AB; 2а > b,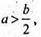 
B > 0, a > 0 але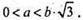 
Відповідь: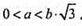 
680.
Проекція многогранника не може мати такий вигляд.
681.
Грані опуклого n-гранника при n = 5 не можуть бути п’ятикутниками,
Якщо він має 2,5n ребер.
682.
Якщо n = 3, то граней 4; n = 5, то граней 6.
683.
Якщо всі грані многогранника – чотирикутники,
То у нього ребер у 2 рази більше, ніж граней.
Наприклад: куб має 6 граней і 12 ребер.
684.
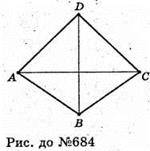
Нехай дано тетраедр ABCD. У тетраедра всі грані – трикутники і всі многогранні кути – тригранні.
Нехай є n-гранник, n = 4. Має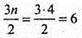 
ребер і n вершин, n = 4.
685.
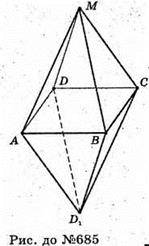
Таким многогранником є октаедр, у нього всі грані – трикутники
І всі многогранні кути – чотиригранні, у нього 8 граней.
686.
Розглядуваний семигранник має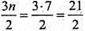 
ребер і
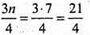– вершин, такого многогранника не існує.
687.
Якщо опуклий многогранник має л вершин, отже, він має n плоских кутів.
Сума всіх плоских кутів дорівнює 360°(n – 2).
688.
Круг, сфера, тригранний кут не є тілами.
(1 votes, average: 5.00 out of 5)
Loading...