Множення звичайних дробів. Властивості множення
Урок № 2 6
Тема. Множення звичайних дробів. Властивості множення
Мета: вдосконалити вміння учнів виконувати завдання, що передбачають виконання множення дробів (на обчислення, спрощення виразів) із урахуванням найраціональнішого способу дій (з використанням властивостей множення).
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань
@ Учитель вибірково перевіряє зошити учнів. “Слабкі” учні перевіряють домашнє завдання біля дошки.
1. Фронтальна
Запитання до класу
– Як виконати множення двох звичайних дробів?
– Як виконати множення натурального числа на звичайний дріб/мішане число?
– Як виконати множення мішаного числа на натуральне (звичайний/мішане) число (дріб / число)?
2. Виконайте дії (найтиповіші, як у домашньому завданні)
І ряд
| II ряд
| III ряд
|
II. Засвоєння знань
Запитання
– Чи можна виконувати множення не двох, а трьох, чотирьох і більше множників?
– Як виконати множення суми на число? (a(b+c) = ab+ ас)
– Чому дорівнює а•0? а•1? 1•а? 0•а?
@ Можливо, на запитання вчителя деякі учні дадуть правильні відповіді, тому вчителеві слід ще раз нагадати, записати закони множення і проілюструвати їх застосування для множення дробів на прикладах.
Конспект 16 | |
Властивості множення | |
1. 2. 3. 4. | Приклади 1. 4. 5. Спростіть: 6. Спростіть: |
@ Як і під час вивчення цього питання відповідно у 5 класі (робота з десятковими дробами), слід наголосити, що застосування законів множення не тільки допомагає виконувати обчислення більш зручним способом, але и допомагає спрощувати вирази
III. Засвоєння вмінь
@ На цьому уроці продовжується (і буде продовжена в інших темах) робота з вироблення стійких умінь учнів, розпочата ще в 5 класі спрощення буквених виразів із застосуванням як сполучної, так і розподільної властивостей множення Новим елементом є множення мішаного числа на натуральне із використанням розподільної властивості множення (це є досить важливим моментом з точки зору автора) Тому досить багато завдань уроку присвячені саме цьому питанню
Усні вправи
І рівень
1. Обчисліть усно, застосувавши розподільний закон множення:
А) 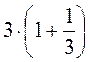 ,
, 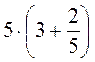 ,
, 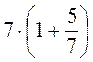 ; б)
; б) 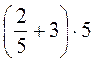 ,
, 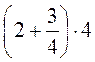 ,
, 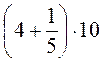 ; в)
; в) 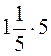 ,
, 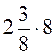 ,
, 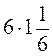 .
.
2. Обчисліть, використовуючи переставну і сполучну властивості множення: а) 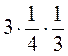 ; б)
; б) 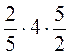 ; в)
; в) 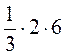 ; г)
; г) 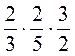 .
.
3. Обчисліть, використовуючи розподільну властивість множення: а) 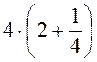 ; б)
; б) 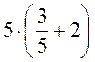 ; в)
; в) 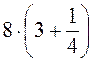 ; г)
; г) 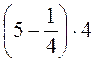 .
.
ІІ, III рівні
Письмові вправи
1. Обчисліть: а) 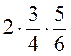 ; б)
; б) 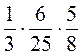 ; в)
; в) 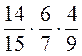 ; г)
; г) 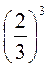 .
.
2. Знайдіть значення виразу: а) 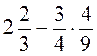 ; б)
; б) 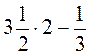 ; в)
; в) 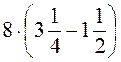 ; г)
; г) 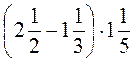 ; д)
; д) 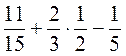 ; е)
; е) 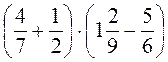 .
.
3. Спростіть вираз: а) 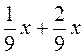 ; б)
; б) 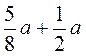 ; в)
; в) 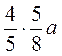 .
.
4. Обчисліть 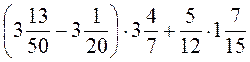 .
.
5. Знайдіть об’єм куба з ребром 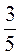 м.
м.
6. Обчисліть: а) 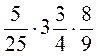 ; б)
; б) 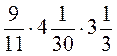 ; в)
; в) 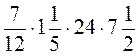 ; г)
; г) 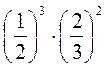 .
.
7. Обчисліть добутки: а) 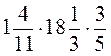 ; б)
; б) 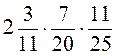 ; в)
; в) 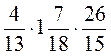 ; г)
; г) 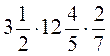 .
.
8. Обчисліть значення виразу: а) 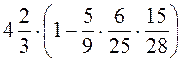 ; б)
; б) 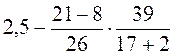 .
.
9. Згадайте, що таке куб числа (а3 = а – а – а). Піднесіть до куба дроби: 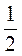 ;
;  ;
; 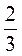 ;
; 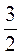 ;
; 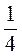 ;
; 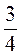 ;
; 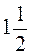 ;
; 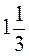 .
.
10. Обчисліть значення виразів а) 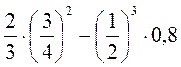 ; б)
; б) 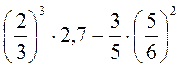 .
.
11. Обчисліть значення виразу: а) 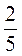 – 0,25х, якщо х =
– 0,25х, якщо х = 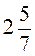 , б) 2 – 3,5 –
, б) 2 – 3,5 – 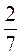 А, якщо а =
А, якщо а = 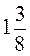 , в) 1
, в) 1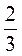 – 0,6х2, якщо х = 0,2.
– 0,6х2, якщо х = 0,2.
Додаткові вправи
1. Використовуючи розподільну властивість множення, знайдіть значення виразу а) 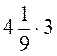 ; б)
; б) 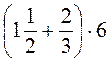 ; в)
; в) 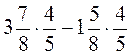 ; г)
; г) 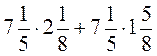 .
.
2. Спростіть вираз: а) 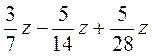 ; б)
; б) 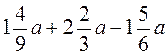 ; в)
; в) 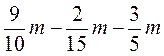 ; г)
; г) 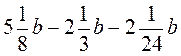 .
.
3. Спростіть вираз а) 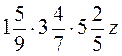 ; б)
; б) 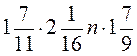 ; в)
; в) 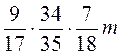 .
.
4. Доведіть, що значення виразу 3,75 – 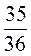 А – 0,75а –
А – 0,75а – 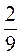 А не залежить від а.
А не залежить від а.
IV. Підсумки уроку
Учні зможуть підбити самі, якщо виконають бліцтест.
1) 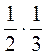 ; 2)
; 2) 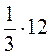 ; 3)
; 3) 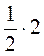 ; 4)
; 4) 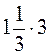 ; 5)
; 5) 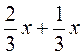 ; 6)
; 6) 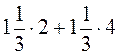 ; 7)
; 7) 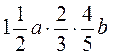 ; 8)
; 8) 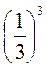 .
.
@ Правильні відповіді шифруються, і в разі правильного виконання завдання учень дістає ключове слово “молодець”.
Відповіді
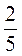
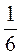
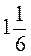
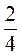
1
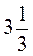
4
Х
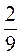 Х
Х
8
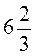
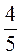 Ab
Ab
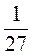
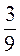
А
Ф
М
К
Н
Л
П
О
Д
Т
Е
X
Ц
Ь
Я
V. Домашнє завдання
1. Обчисліть (усно): а) 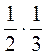 ; б)
; б) 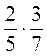 ; в)
; в) 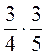 ; г)
; г) 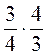 .
.
2. а) 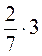 ; б)
; б) 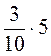 ; в)
; в) 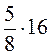 ; г)
; г) 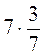 .
.
3. Обчисліть, використовуючи переставну і сполучну властивості множення (усно): а) 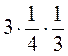 ; б)
; б) 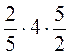 ; в)
; в) 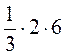 ; г)
; г) 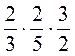 .
.
4. Обчисліть, використовуючи розподільну властивість множення: а) 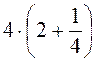 ; б)
; б) 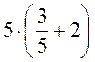 ; в)
; в) 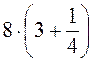 ; г)
; г) 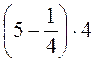 .
.
5. Знайдіть значення виразу: а) 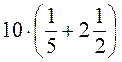 ; б)
; б) 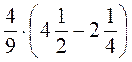 ; в)
; в) 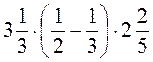 .
.
6. Спростіть вираз: а) 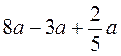 ; б)
; б) 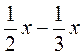 ; в)
; в) 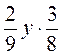 .
.
7. Розв’яжіть рівняння: 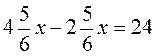 .
.
8. Обчисліть: а) 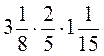 ; б)
; б) 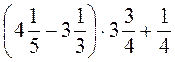 ; в)
; в) 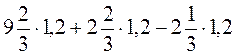 .
.
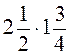
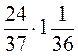
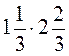
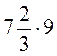
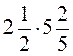
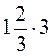
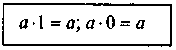
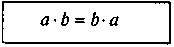
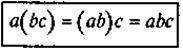
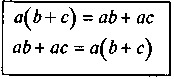
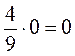 ; 2.
; 2. 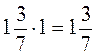 ; 3.
; 3. 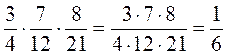 ;
;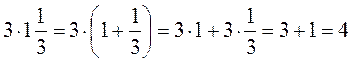 .
.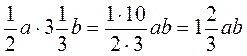 .
.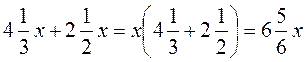 .
.