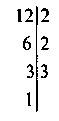Найбільший спільний дільник кількох чисел
Урок № 5
Тема. Найбільший спільний дільник кількох чисел
Мета: на основі знань про дільник числа сформувати поняття учнів про спільний дільник двох (трьох і т. д.) чисел і найбільший спільний дільник, а також розглянути алгоритм знаходження НСД кількох чисел; сформувати початкові вміння учнів виконувати базові завдання, що передбачають використання алгоритму знаходження НСД.
Тип уроку: засвоєння знань і формування початкових умінь.
Хід уроку
І. Перевірка домашнього завдання. Актуалізація опорних знань і вмінь
1. Учитель
2. Після перевірки домашнього завдання можна запропонувати самостійну роботу. Знайдіть серед розкладів неправильний:
72 = 23 – 32; 84 = 22 – 3 – 7; 90 = 22 – 32 – 5.
(Це розклад 90 = 22 – 32 – 5, правильно -90 = 2 – 32 – 5)
II. Формування нових знань
1. Постановка проблеми
Задача. З 18 цукерок, 12 яблук треба зробити гостинці для першокласників, щоб у кожному гостинці цукерок і яблук була однакова кількість. Скількох першокласників
@ Аналіз умови приводить до висновку, що під час розв’язування треба знайти числа, на які ділилися б і 18, і 12.
2. Розв’язування проблеми
Учні знайомляться з поняттям:
– спільного дільника,
– найбільшого спільного дільника двох, трьох чисел і т. д.;
– алгоритмом знаходження НСД;
– поняттям взаємно простих чисел, виконуючи короткі записи в зошиті (конспекті 4) або працюючи з таблицею.
.
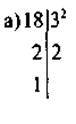
Конспект 4 НСД (а; b) 1) 18 ділиться на: 1; 2; 3; 6; 9; 18. 12 ділиться на: 1; 2; 3; 4; 6; 12.
2) Як знайти НСД (18; 12) з їх розкладів на прості множники? | ||
|
| Б) 18 = 2 – 32; 12 = 22 – 3; В) НСД (18; 12) = 2 – 3 = 6 |
3) Якщо НСД (а; b) = 1, то а і b – взаємно прості. Приклад: а = 2 – 3 – 5; b = 7 – 11 – 13. НСД (а; b) = 1; а, b – взаємно прості |
III. Закріплення знань учнів, формування вмінь
1. Яке число називається НСД двох натуральних чисел?
2. Які два числа називаються взаємно простими?
3. Знайдіть НСД (a; b), якщо:
А) а = 2 – 3; b = 2 – 5;
Б) а =22 – 3 – 5; b = 22 – 32;
В) а = 2 – 3 – 7; b = 52.
Чи можна за цим самим алгоритмом знайти НСД трьох чисел?
Письмові вправи
1. Знайдіть усі спільні дільники чисел: а) 50 і 40; б) 56 і 98.
2. Знайдіть НСД чисел: а) 253 і 207; б) 50 і 49; в) 120; 180; 200.
3. Доведіть, що числа 36 і 77 взаємно прості.
@ Після виконання цього завдання доречно буде зауважити, що поняття прості числа і взаємно прості числа не слід плутати.
Якщо вистачає часу, можна розв’язати додаткові завдання.
Додаткові вправи
1. Діти отримали на новорічній ялинці однакові подарунки. У всіх подарунках разом було 123 апельсини і 82 яблука. Скільки дітей було присутньо на святі? Скільки апельсинів і скільки яблук було в кожному з подарунків?
2. Запишіть усі правильні дроби зі знаменником 12, у яких чисельник і знаменник – взаємно прості числа.
3. Знайдіть значення виразу: 1,24 : 3,1 + 12 : 0,25 – 2 : 25 + 1,8 : 0,45.
IV. Підсумки уроку
(Див. усні вправи)
V. Домашнє завдання
1. Знайдіть найбільший спільний дільник чисел:
а) 30 і 70; б) 42 і 48; в) 120 і 160.
2. Знайдіть найбільший спільний дільник трьох чисел: 26, 39 і 52.
3. Які зданих пар чисел взаємо прості: а) 16 і 9; б) 18 і 81; в) 11 і 121?
4. У двох ящиках 53 кг яблук. Скільки яблук у кожному ящику, якщо
в першому їх на 5 кг більше, ніж у другому?