Описані і вписані кола
Розділ 1. Найпростіші геометричні фігури та їх властивості
§ 17. Описані і вписані кола
671. Коло, описане навколо трикутника, зображено на мал. 372.
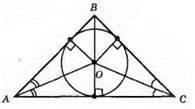
672. Коло, вписане у трикутник, зображено на мал. 375.
673.
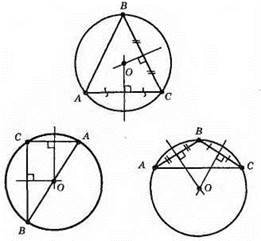
Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника.
Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи.
Центр кола, описаного навколо тупокутного трикутника, лежить поза трикутником.
674.
675.
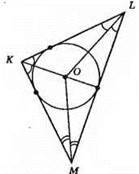
676. 1)
Через одну точку можна провести безліч кіл.
2)
Через дві точки можна провести безліч кіл.
3)
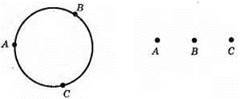
Через три точки можна провести одне коло, або жодного, якщо точки лежать на одній прямій.
677.
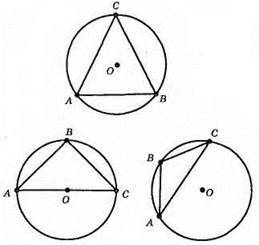
678. Так, бо прямі, що містять медіани рівностороннього трикутника, є серединними перпендикулярами до сторін трикутника.
679. Радіус

680.
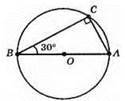
Оскільки АС = 10 см, то AB = 2АС = 2 х 10 см = 20 см.
Тоді 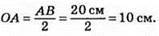
Відповідь: 10 см.
681.
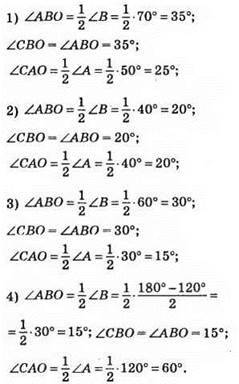
682.
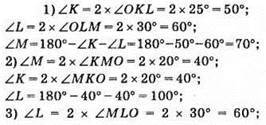
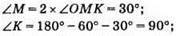
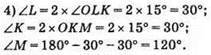
683.
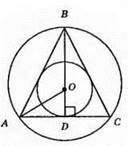
?AOD – прямокутний.
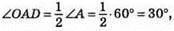 тоді
тоді 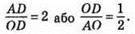
684.
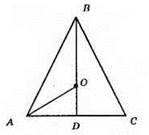
Оскільки OB = AO = R, a OD = r, то BD = BO + OD = R + r.
685.
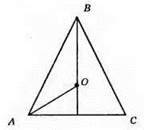
Радіус кола, описаного навколо рівностороннього трикутника, дорівнює 2/3 його висоти. 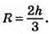
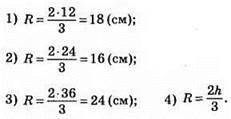
686. Радіус кола, вписаного в рівносторонній трикутник, дорівнює 1/3 висоти: h/3.
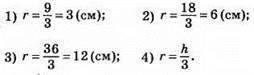
687. Точка перетину серединних перпендикулярів двох сторін трикутника лежить на його третій стороні, якщо цей трикутник прямокутний.
688.
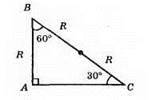
Так, якщо один із кутів дорівнює 30°.
689.
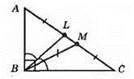
?ВМС – рівнобедрений (ВМ = MC). ∠МВС = 45° – 10° = 35°, ∠C = ∠MBC = 35°. ∠A = 90° – 35° = 55°.
690.
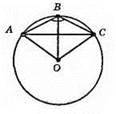
?АВО і? ВОС – рівносторонні, тому R = BO = BC= AB = АО = 6 см.
691.
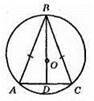
Нехай? ABC – рівнобедрений (AB = BC). Проведемо серединний перпендикуляр до основи АС, тоді центр кола, описаного навколо трикутника ABC, буде лежати на прямій BD. Оскільки BD ⊥ АС, то BD – бісектриса кута В.
692.
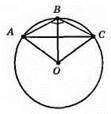
АВ = ВС = 4 см. ∠ABC = 120°. Оскільки? ВОС = ?АВO і ці трикутника рівносторонні, то R = АО = ВО = СО = ВС = АВ = 4 см.
693.
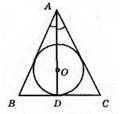
Нехай? ABC – рівнобедрений (AB = АС). Проведемо бісектрису кута А (кута, протилежного до основи), на якій лежить центр О – кола, вписаного у трикутник ABC. Оскільки AD – бісектриса рівнобедреного трикутника, то AB – медіана.
694.
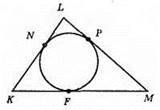
?KLM – рівнобедрений, KL = LM, N, P, F – точки дотику.
KN = 8 см, NL = 4 см.
KL = KN + NL = 8 + 4 = 12 (см); LM = KL = 12 см. KM = 2KF = 2 x 8 = 16 (см).
P? KLM = 12 + 12 + 16 = 40 (см).
Відповідь: 40 CM.
695.
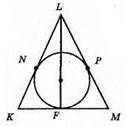
?KLM – рівнобедрений, KL = LM, N, P, F – точки дотику.
KN : NL = 5 : 7, KM = 10 см.
KF = FM = 10 см: 2 = 5 см.
KN = KF = 5 см; NL = 7 см; KL = 12 см; LM = 12 см.
P? KLM= 12 + 12 + 10 = 34 (см).
Відповідь: 34 см.
696.
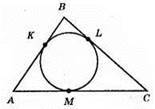
K, L, М – точки дотику, KВ = 4 см, АК = 5 см, MC = 6 см.
AB = AK + KB = 5 см + 4 см = 9 см.
BL = BK = 4 см, LC = MC = 6 см, BC = BL + LC = 4 см + 6 см = 10 см, AM = AK = 5 см, AC = 5 см + 6 см = 11 см.
Відповідь: 9 см, 10 см, 11 см.
697.
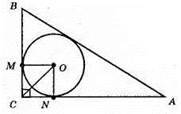
Оскільки CO – бісектриса кута С, то ∠BCO = ∠ACO = 45°.
?СОМ і? CON – прямокутні і рівнобедрені (оскільки ∠СОМ = 90° – 45° = 45°, ∠CON = 90° – 45° = 45°), то CM = CN = OM = ON.
698. Р = 2m + 2n + 2r = 2(m + n + r).
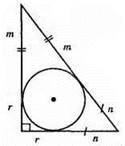
1) 2 х (4 + 6 + 2) = 2 х 12 = 24 (см);
2) 2 х (3 + 10 + 2) = 2 х 15 = 30 (см);
3) 2 х (5 + 12 + 3) = 2 х 20 = 40 (см);
4) 2 х (4 + 21 + 3) = 2 х 28 = 56 (см).
699.
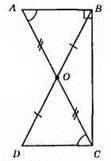
Нехай О – середина гіпотенузи АС, ВО – медіана трикутника ABC. Продовжимо її так, що DO = ВО,
?АОВ = ?COD (за першою ознакою рівності трикутників: AO = CO, ВО = OD, ∠AOB = ∠COD – як вертикальні кути). Із рівності трикутників маємо: AB = CD, ∠BAO = ∠DCO.
Оскільки ∠BAO = ∠DCO і ці кути внутрішні різносторонні при прямих AB i CD і січній АС, то прямі AB і CD паралельні. Оскільки AB ⊥ ВС і DC || AB, то DC ⊥ BC.
?АВС = ?DCB, тоді АС = DB. Звідси 1/2AC = 1/2DB, тобто АО = ВО.
Оскільки АО = ВО = СО, то О – центр кола, описаного навколо трикутника ABC.
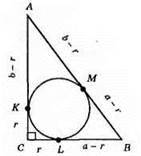
700. Нехай АС = b, СВ = а, AB = с. К, L, М – точки дотику, тоді КС = CL = r, LВ = а – r, АВ = b – r, МВ = а – r.
С = AM + MB = b – r + a – r = a + b – 2r.
Звідси 2r = а + b – с, 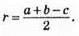
701.
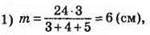
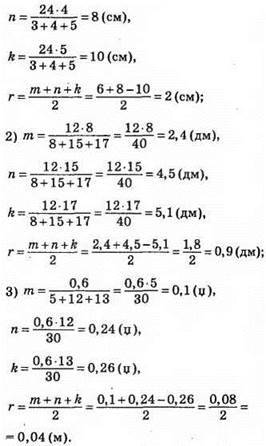
702.
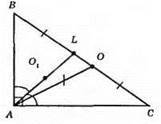
?АВС – прямокутний, ∠A = 90°. О – центр описаного кола, О1 – центр вписаного кола, тоді АО – медіана, AL – бісектриса, ∠LAO = 7°.
?АОС – рівнобедрений (АО = ОС), ∠OAC = ∠OCA = 45° – 7° = 38°.
?ВОА – рівнобедрений (АО = OB). ∠ABO = ∠BAO = 45° + 7° = 52°.
Відповідь: 38°, 52°.
703.
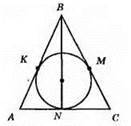
Оскільки AK = AN, ВМ = BK, CN = СМ, то додавши почленно три рівності, одержимо: AK + ВМ + CN = AN + ВК + СМ.
704. Оскільки Р = AB + ВС + АС = (AK + KB) + ВС + (AN + CN) = AK + BC + (KB + CN) + AN = AK + BC + (MB + MC) + AN = AK + BC + BC + AN = AK + 2BC + AN.
Враховуючи, що AK = AN, P = 2p, маємо: 2p = 2AK + 2 BC, p = AK + BC, AK = p – BC. Отже, AK = AN = p – BC.
705.
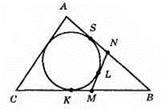
P? BMN = MN + NB + MB = NL + LM + NB + MB = SN + KM + NB + MB = (SN + NB) + (KM + MB) = SB + KB = AB = a.
706.
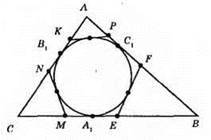
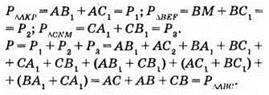
/p>
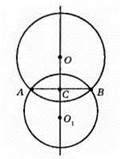
Нехай коло з центром О проходить через точки А і В, тоді ОС ⊥ АВ, АС = СВ, отже, точка О лежить на серединному перпендикулярі.
Якщо точка О лежить на серединному перпендикулярі ОС, то існує коло з центром О, яке проходить через точки А і В. Отже, геометричним місцем центрів кіл, які проходять через дані точки А і В, є серединний перпендикуляр до відрізка AB.
657.
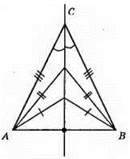
Геометричним місцем вершин рівнобедрених трикутників, що мають спільну основу АB, є серединний перпендикуляр до відрізка AB за винятком точки, яка є серединою відрізка AB.
658.
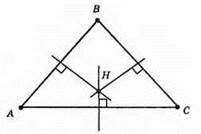
Геометричним місцем точок, рівновіддалених від усіх вершин трикутника, є точка перетину серединних перпендикулярів до сторін трикутника.
659.
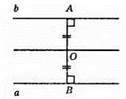
Геометричним місцем точок, рівновіддалених від двох паралельних прямих, є пряма, яка паралельна даним прямим і проходить через середину відрізка, перпендикулярного даним прямим і з кінцями на даних прямих.
660.
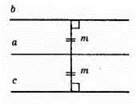
Геометричним місце точок, віддалених від прямої а на відстань m, є дві прямі, які лежать по різні сторони від прямої а, які паралельні прямій а і знаходяться від прямої а на відстані m.
661.
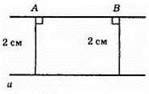
Ні, оскільки існують інші точки (наприклад усі точки прямої AB відмінні від точок відрізка AB), які віддалені від прямої а на 2 см.
662.
Геометричним місцем центрів кіл радіуса R, що дотикаються до прямої а, є дві прямі (які лежать по різні боки від прямої а), які паралельні прямій а і віддалені від прямої а на R.
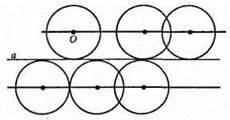
663.
Геометричним місцем вершин трикутників зі спільною стороною AB і бічною стороною, що дорівнює а, є коло з центром у точці В із радіусом а, за винятком двох точок перетину прямої AB та кола.
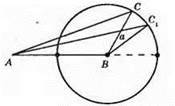
664.
Геометричним місцем центрів кіл, які дотикаються до двох даних кіл з центрами в точках О і O1 і рівними радіусами, є серединний перпендикуляр до відрізка OO1.
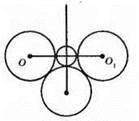
665.
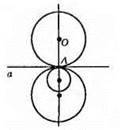
Геометричним місцем центрів кіл, що дотикаються до прямої а в точці А, є перпендикулярна пряма до прямої а, яка проходить через точку А.
666.
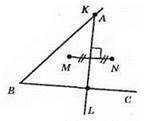
Шукані точки К і L – це точки перетину серединного перпендикуляра до відрізка MN і сторін кута.
Задача має один розв’язок, якщо серединний перпендикуляр до MN паралельний одній зі сторін кута або збігається з бісектрисою кута ABC. В усіх інших випадках задача має два розв’язки.
667.
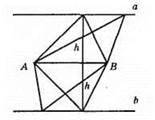
Геометричним місцем вершин трикутників, що мають спільну основу AB і однакову висота h, проведену до цієї сторони, є дві прямі, які паралельні AB і знаходяться на відстані h від AB.
668.
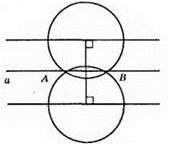
Геометричним місцем центрів кіл радіуса R, які відтинають на даній прямій а хорду даної довжини l, є:
1) дві прямі, паралельні даній прямій, якщо l < 2R;
2) дана пряма, якщо l = 2R;
3) якщо l > 2R, то такого геометричного місця точок не існує.