Головна ⇒ 📌Довідник з геометрії ⇒ Теорема про триперпендикуляри
Теорема про триперпендикуляри
Геометрія
Стереометрія
Теорема про триперпендикуляри
Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
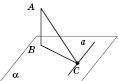
Приклади застосування теореми про три перпендикуляри
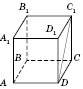
1. На рисунку 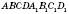 – куб.
– куб.
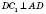 , тому що:
, тому що:
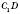 – похила,
– похила,СD – проекція.
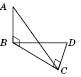
2. На рисунку
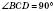 , тоді, тобто AC є відстанню від точки A до прямої CD.
, тоді, тобто AC є відстанню від точки A до прямої CD.AB – перпендикуляр,
AС – похила,
BС – проекція.
3. На рисунку ABCD – прямокутник, у даному випадку квадрат.
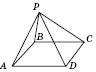
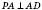 ;
; 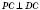 .
.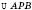 ,
, 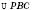 ,
, 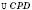 ,
,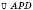 – прямокутні.
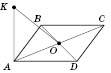
– прямокутні.4. На рисунку ABCD – ромб.
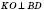 .
.
5. На рисунку нижче
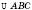 – рівнобедрений, .
– рівнобедрений, .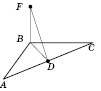
BD – бісектриса (медіана, висота),
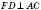 .
.FB – перпендикуляр,
FD – похила,
BD – проекція.
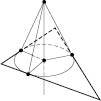
Теорема 2. Пряма, перпендикулярна до площини трикутника і проведена через центр вписаного в нього кола (див. рисунок), є геометричним місцем точок простору, рівновіддалених від сторін трикутника.




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Кут між мимобіжними прямими Геометрія Стереометрія Кут між мимобіжними прямими Дві прямі, що перетинаються, утворюють суміжні та вертикальні кути. Кутова міра меншого із суміжних кутів називається Кутом між прямими. Кут між перпендикулярними прямими дорівнює за означенням. Кут між паралельними прямими вважаємо таким, що дорівнює нулю. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються й паралельні даним мимобіжним […]...
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Урок 31 Тема. Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Мета уроку: формування понять: перпендикуляр до площини, похила, основа похилої, основа перпендикуляра, проекції похилої на площину, відстань від точки до площини. Виявлення взаємозв’язку між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій. […]...
- Ознака паралельності прямої і площини Геометрія Стереометрія Ознака паралельності прямої і площини Теорема 1. Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Теорема 2. Якщо пряма паралельна площині, то на цій площині знайдеться пряма, яка паралельна даній прямій. Зверніть увагу: паралельність прямої і площини не означає, що ця пряма паралельна […]...
- Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Перпендикуляр і похила. Розв’язування задач Урок № 36 Тема. Перпендикуляр і похила. Розв’язування задач Мета: сформувати в учнів свідоме розуміння змісту понять похилої до прямої, проекції похилої на пряму, а також властивостей перпендикуляра, похилих та їх проекцій. Сформувати вміння: – відтворювати зміст вивчених понять; – знаходити названі геометричні об’єкти на рисунку; – виконувати рисунок із зображенням названих об’єктів за даним […]...
- Ознака паралельності площин Геометрія Стереометрія Ознака паралельності площин Теорема 1. Якщо дві прямі однієї площини, які перетинаються й відповідно паралельні двом прямим другої площини (див. рисунок), то ці площини паралельні. Теорема 2 (обернена). Якщо в одній площині є дві прямі, які перетинаються, і ці прямі паралельні другій площині, то такі площини паралельні. Зверніть увагу: прямі мають обов’язково перетинатися. […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- Теорема Фалеса Геометрія Чотирикутники Теорема Фалеса Теорема 1 (Фалеса). Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки й на другій його стороні. На рисунку ; ; . Зверніть увагу: . Теорема має місце не тільки для сторін кута, а й для довільних прямих. Теорема 2 (про […]...
- Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Урок 8 Тема. Теорема про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій Мета уроку: вивчення теореми про існування і єдність прямої, яка проходить через дану точку і паралельна даній прямій. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Фронтальне опитування. 1) Які прямі в просторі називаються паралельними? 2) Вкажіть […]...
- Кут між мимобіжними прямими Урок 53 Тема. Кут між мимобіжними прямими Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими. Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда. Хід уроку II. Перевірка домашнього завдання В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання. III. Сприйняття й […]...
- Властивість точки, рівновіддаленої від вершин многокутнику Урок 32 Тема. Властивість точки, рівновіддаленої від вершин многокутнику Мета уроку: формування знань про властивість точки, рівновіддаленої від вершин многокутника, та вмінь застосовувати цю властивість до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, описане навколо многокутника”. Хід уроку 1. Перевірити розв’язання задачі № 24 за записами (з пропусками), зробленими на дошці до початку уроку. Розв’язання […]...
- Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Середня лінія трикутника Геометрія Трикутники Середня лінія трикутника Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін. Теорема 1. Середня лінія трикутника, яка сполучає середини двох його сторін, паралельна третій стороні й дорівнює її половині. На рисунку праворуч: ;. У трикутнику можна провести три середні лінії. Вони утворюють трикутник з такими ж кутами, як даний, і […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Зображення просторових фігур на площині Геометрія Стереометрія Зображення просторових фігур на площині Для зображення просторових фігур на площині, як правило, користуються Паралельним проектуванням. Беремо довільну пряму h, яка перетинає площину рисунка , проводимо через довільну точку A фігури пряму, паралельну h. Точка перетину цієї прямої з площиною рисунка буде зображенням точки A. Побудувавши таким чином зображення кожної точки фігури, дістанемо […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- ПОХИЛА ПЛОЩИНА – ПРОСТІ МЕХАНІЗМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ 3.8. ПРОСТІ МЕХАНІЗМИ 3.8.3. ПОХИЛА ПЛОЩИНА Щоб тіло, яке перебуває на похилій площині, було в стані спокою і рівномірного (без тертя) руху, необхідно прикласти силу, паралельну похилій площині і в стільки ж разів меншу від сили тяжіння, у скільки разів висота похилої площини […]...
- Площа ортогональної проекції многокутника Урок 56 Тема. Площа ортогональної проекції многокутника Мета уроку: вивчення теореми про площу ортогональної проекції многокутника, формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 42, 45 на дошці. 2. Фронтальне опитування. 1) Дайте означення кута між двома площинами, які перетинаються. […]...
- Властивості паралельних площин Геометрія Стереометрія Властивості паралельних площин Теорема 1. Якщо дві паралельні площини перетинаються третьою площиною (див. рисунок), то прямі перетину паралельні. На рисунку: ; . Теорема 2. Відрізки паралельних прямих, які містяться між двома паралельними площинами (див. рисунок), рівні. На рисунку: ; ; . Теорема 3. Нехай площини і паралельні (див. рисунок нижче) і є точка […]...
- Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
- Проекція вектора на координатну вісь – Елементи векторної алгебри 3. Елементи векторної алгебри 3.5. Проекція вектора на координатну вісь Довжину відрізка A1B1 між проекцією початку вектора а і кінця вектора на вісь, взяту зі знаком ” + ” або “-“, називають проекцією вектора на координатну вісь. Проекція додатна, коли напрям руху від проекції початку вектора до проекції кінця збігається із напрямом координатної осі, і […]...
- Перпендикулярні площини. Ознака перпендикулярності площин Урок 38 Тема. Перпендикулярні площини. Ознака перпендикулярності площин Мета уроку: формування поняття перпендикулярності площин. Вивчення ознаки перпендикулярності площин. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Перевірити виконання задач № 49, 50 за записами, зробленими до початку уроку на дошці. Нехай AB?; А?, d?; АВ = b, ACD, AC = a (рис. […]...
- Тематичне оцінювання № 4 Урок 43 Тема. Тематичне оцінювання № 4 Мета уроку: перевірка навчальних досягнень учнів з теми “Перпендикулярність прямих і площин у просторі”. Хід уроку Тематичне оцінювання № 4 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 4 Варіант А Варіант 1 1. Побудуйте зображення куба ABCDA1B1C1D1 і запишіть грані куба, які перпендикулярні […]...
- Тематичне оцінювання № 3 Урок 34 Тема. Тематичне оцінювання № 3 Мета уроку: перевірка навчальних досягнень учнів з тем “Перпендикулярність прямих”, “Перпендикулярність прямої і площини”. Хід уроку Тематичне оцінювання № 3 можна провести у вигляді тематичної контрольної роботи. 1. Тематична контрольна робота № 3 Варіант А 1. Користуючись зображенням куба ABCDA1B1C1D1 (рис. 180), запишіть ребра куба, які перпендикулярні до […]...
- Теорема косинусів УРОК № 4 Тема. Теорема косинусів Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її. Хід уроку I. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Теорема Піфагора Урок № 34 Тема. Теорема Піфагора Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв’язування задач на знаходження невідомих сторін прямокутних трикутників. Типу уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Властивості прямої і площини, перпендикулярних між собою Урок 30 Тема. Властивості прямої і площини, перпендикулярних між собою Мета уроку: формування знань учнів про властивості перпендикулярних прямих і площин. Обладнання: стереометричний набір, схема “Властивості прямо і площини, перпендикулярних між собою” (с. 116). Хід уроку І. Перевірка домашнього завдання 1. Колективне обговорення розв’язування задачі № 10. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Розв’язування задач на знаходження кутів у просторі Урок 57 Тема. Розв’язування задач на знаходження кутів у просторі Мета уроку: формування вмінь учнів знаходити кути у просторі. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 48 (2) 49 (1) на дошці. 2. Фронтальне опитування. 1) Сформулюйте теорему про площу ортогональної проекції многокутника. 2) Знайдіть площу ортогональної проекції […]...
- Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...
« КАЗНА