Основні властивості хвильової моделі
БУДОВА АТОМА
6 . Хвильова модель
Суперечливість теорії Бора вдалося усунути за допомогою поданих Е. Шредингером і В. Гейзенбергом уявлень, зберігаючи при цьому основну ідею теорії квантів:
– припущення про рух електрона з певною швидкістю по постійній орбіті суперечить принципу невизначеності Гейзенберга. Даний принцип стверджує, що неможливо абсолютно точно визначити одночасно положення і швидкість електрона;
– електрону відводиться не якась певна орбіта, а простір, в якому він може знаходитися, так звана електронна
– електронна хмара є тривимірним простором місцезнаходження електронів, які, за Шредингером, можна описати математичними функціями (хвильовими функціями);
– квадрат хвильової функції визначає ймовірність знаходження електрона у хмарі.
Запам’ятайте: орбіталь є обмеженим простором, у якому ймовірність знаходження електрона максимальна (приблизно 90 %).
6.1. Основні властивості хвильової моделі
Для опису енергетичних рівнів електрона на додаток до теорії Бора використовують чотири квантових числа.
– Головне квантове число n позначає енергетичний рівень електронної орбіталі.
– Побічне квантове (орбітальне) число l характеризує різницю енергій всередині одного енергетичного рівня і просторову форму орбіталі.
– Магнітне квантове число m визначає просторову орієнтацію електронних орбіталей атома під впливом зовнішнього магнітного поля.
– Спінове квантове число s враховує різні власні напрями обертання електронів, так званий спін.
Чотири квантових числа можуть набувати лише певних значень, які відповідають так званим правилам відбору.
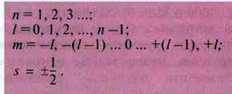
Чотири квантових числа однозначно описують кожен електрон атома. Це можна порівняти з однозначно закріпленими телефонними номерами, що ніколи не повторюються.
Стосовно електронів в одному атомі В. Паулі сформулював у 1925 р. принцип, названий його ім’ям, принцип Паулі:
Електрони атома повинні відрізнятися між собою, як мінімум, одним квантовим числом.
Запам’ятайте: на кожній орбіталі можуть знаходитися два електрони з різним спіном 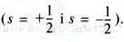
Комбінація всіх чотирьох квантових чисел для n = 1 – 3 обумовлює таку заселеність електронів:
Головне квантове число n | Побічне квантове число l | Магнітне квантове число m | Спінове квантове число s |
N = 1, 2, 3 … | L = 0, 1, 2… (n – 1) | M = – l…0…+l | S = ± 1/2 |
1 | 0 | 0 | ±1/2 |
2 | 0 | 0 | ±1/2 |
1 | -1 | ±1/2 | |
0 | ±1/2 | ||
+1 | ±1/2 | ||
3 | 0 | 0 | ±1/2 |
1 | -1 | ±1/2 | |
0 | ±1/2 | ||
+1 | ±1/2 | ||
2 | -2 | ±1/2 | |
-1 | ±1/2 | ||
0 | ±1/2 | ||
+1 | ±1/2 | ||
+2 | ±1/2 |
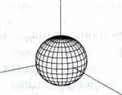
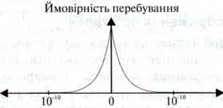
Орбіталі з побічним квантовим числом l = 0 мають сферично-симетричну просторову структуру, ймовірність перебування електронів усередині орбіталі є більшою поблизу атомного ядра, та в міру віддалення від атомного ядра вона зменшується.
Запам’ятайте: орбіталі з l = 0 називають s-орбіталями.
Орбіталі з побічним квантовим числом l = 1 мають просторову структуру у формі гантелі. Відповідно до правил відбору існують три можливих магнітних квантових числа зі значеннями -1, 0, +1. Їм відповідають три орбіталі в трьох напрямах.
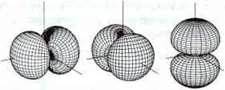
Запам’ятайте: орбіталі з l = 1 називають р-орбіталями.
Орбіталі з побічним квантовим числом l = 2 мають просторову структуру у формі розетки. Відповідно до правил відбору отримуємо п’ять можливих магнітних квантових чисел зі значеннями -2, -1, 0, +1, +2. Їм відповідають п’ять орбіталей.
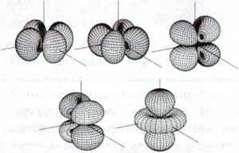
Запам’ятайте: орбіталі з l = 2 називають d-орбіталями.