Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування
Урок № 48
Тема. Означення квадратного рівняння. Неповні квадратні рівняння та їх розв’язування
Мета: закріпити знання учнів щодо означення квадратного рівняння, коефіцієнтів квадратного рівняння та його видів; домогтися засвоєння учнями способів розв’язання неповних квадратних рівнянь; сформувати вміння застосовувати вивчений матеріал для розв’язування неповних квадратних рівнянь.
Тип уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект “Квадратні рівняння”.
Хід уроку
I. Організаційний
II. Перевірка домашнього завдання
Математичний диктант
Варіант 1 | Варіант 2 |
1. Запишіть квадратне рівняння | |
Перший коефіцієнт дорівнює 3; Другий коефіцієнт дорівнює – 5; Вільний член – 0 | Перший коефіцієнт дорівнює – 5; Другий коефіцієнт дорівнює 3; Вільний член – 0 |
2. Запишіть зведене квадратне рівняння, другий коефіцієнт якого і вільний член дорівнюють | |
-2 | -3 |
3. Запишіть неповне квадратне рівняння зі змінною t: | |
Перший | Перший коефіцієнт дорівнює – 3, вільний член – 5 |
4. Запишіть неповне квадратне рівняння: | |
Перший коефіцієнт дорівнює 8, Другий коефіцієнт – 5 | Перший коефіцієнт дорівнює 5, Другий коефіцієнт – 7 |
III. Формулювання мети і завдань уроку
Тема розділу сама по собі створює мотивацію навчальної діяльності учнів і визначає мету уроку: після засвоєння на попередньому уроці видів неповних квадратних рівнянь на цьому уроці слід вивчити способи розв’язання таких видів рівнянь.
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння учнів: виконання тотожних перетворень цілих виразів, розкладання многочленів на множники, добування квадратного кореня з числа, розв’язування рівнянь виду х2 = а.
Виконання усних вправ
1. Обчисліть: а) 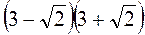 ; б)
; б) 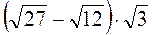 ; в)
; в) 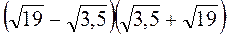 ; г)
; г) 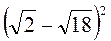 .
.
2. Укажіть, чому дорівнюють перший і другий коефіцієнти та вільний член квадратного рівняння:
A) х2 – 4х + 1 = 0; б) 3х – х2 – 6 = 0; в) 2х2 – 7х = 0; г) х2 – 8 = 0; д) 11х2 = 0.
3. Розв’яжіть рівняння:
А) х2 = 4; б) х2 = 2; в) х2 =0; г) х2 – 3 = 0; д) 2х2 – 8 = 0; е) х2 + 4 = 0; ж) х(х – 1) = 0; з) 3х(х + 2) = 0; и) 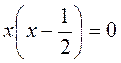 .
.
V. Засвоєння знань
План вивчення нового матеріалу
1. Схема розв’язання рівняння виду ах2 + bх = 0.
2. Схема розв’язання рівняння виду ах2 + с = 0.
3. Схема розв’язання рівняння виду ах2 = 0.
@ Насправді навчальний матеріал уроку не містить нових для учнів відомостей. На уроці систематизуються та приводяться у відповідність до нової термінології відомості про вивчені у 7 та у 8 класах способи розв’язання неповних квадратних рівнянь.
VI. Формування вмінь
Виконання усних вправ
1. Укажіть, чому дорівнює кожний із коефіцієнтів квадратного рівняння: а) 5х2 – х + 1 = 0; б) 4х – х2 + 4 = 0; в) 3х2 + 7х = 0; г) 3х2 – 4 = 0; д) 12х2 = 0.
Які з цих рівнянь є неповними квадратними рівняннями?
2. Які рівняння не мають коренів?
А) х2 – х = 0; б) х2 = 0; в) 2х2 = -8; г) – 3х2 = -1; д) – х2 – 3х = 0.
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв’язати завдання такого змісту:
1. Розв’язування неповних квадратних рівнянь.
1) Розв’яжіть рівняння: а) х2 – 36 = 0; б) 2х2 – 4 = 0; в) х2 + 49 = 0.
2) Розв’яжіть рівняння: а) х2 – 3х = 0; б) -5х2 + 20х = 0; в) х2 + 3,5х = 0.
3) Розв’яжіть рівняння: а) 3х2 – 4х = 0; б) -5х2 + 6х = 0; в) 10х2 + 7х = 0; г) 4a2 – 3a = 0; д) 6z2 – z = 0; e) 2y + y2 = 0.
4) Знайдіть корені рівняння: а) 4х2 – 9 = 0; б) – х2 + 3 = 0; в) -0,1х2 + 10 = 0; г) 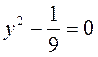 ; д) 6v2 + 24 = 0; є) 3m2 – 1 = 0.
; д) 6v2 + 24 = 0; є) 3m2 – 1 = 0.
2. Розв’язування рівнянь, що зводяться до неповних квадратних рівнянь шляхом застосування властивостей рівносильних перетворень.
1) Розв’яжіть рівняння: а) 7 – 2х2 = 7 + 0,5х2; б) 2х2 – 3х = 2х; в) 2х(х – 3) = х2.
2) Розв’яжіть рівняння:
А) х2 – 13х + 8 = 3х2 – 13х;
Б) х(х + 1) = х + 24;
В) 2х2 – (5х – 1) = 17 – 5х;
Г) 0,3х(х – 4) + 1,2х – 2,7 = 0.
3) Знайдіть корені рівняння:
А) 5х2 – 7х + 3 = 3х2 + 2х + 3;
Б) 4 – 6х – х2 = 9х2 + х + 4;
В) 2(х2 + х – 3) = 5х2 – 6;
Г) (х + 2)2 + (х – 2)2 = 3х2 – 9;
Д) 6х2 + 9x – 1 = (2x + 1)(2x – 1);
Є) 4(х2 – 2) = х(1 – х) – 8;
Ж) 0,2х2 – х(0,5х – 1) = х – 9; з) 0,3х(х – 4) + 1,2х – 2,7 = 2,7.
4) Знайдіть корені рівняння:
А) (х + 3)(х – 4) = -12;
Б) 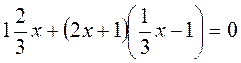 ;
;
В) (3х – 1)2 – 1 = 0;
Г) 3х(2х + 3) = 2х(х + 4,5) + 2;
Д) 18 – (х – 5)(х – 4) = – х2;
E) (x – 1)(х + 1) = 2(x2 – 3).
3. Знаходження значень змінних, при яких значення виразу дорівнює даному числу, або складання неповного квадратного рівняння, що відповідає текстовій задачі.
1) Знайдіть значення х, при яких значення виразу 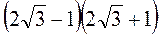 дорівнює 17.
дорівнює 17.
2) При яких значеннях х значення виразу х2 – 5х + 7 на 4 більше від значення виразу 2х2 + 4х + 3?
3) Знайдіть усі числа, які у 17 разів менші від їхніх квадратів.
4) Добуток двох послідовних цілих чисел у 1,5 рази більше від квадрата меншого із них. Знайдіть ці числа.
5) Якщо від квадрата відрізати трикутник площею 59 см2, то площа тієї частини, що залишилась, дорівнює 85 см2. Знайдіть сторону квадрата.
4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань (розв’язати неповне квадратне рівняння з параметром).
1) При яких значеннях а число 2 є коренем рівняння:
А) а2х2 – 7х + 3а + 14 = 0;
Б) ах2 + ах – 2 = 0?
2) Розв’яжіть рівняння з параметром а: а) ах2 + 1 = 0; б) х2 – 2ах = 0; в) ах2 – а3 = 0.
3) Знайдіть пропущений вираз:
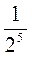
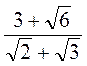
?
5. На повторення: завдання на виділення повного квадрата двочлена з даного квадратного тричлена (з парним та непарним другим коефіцієнтом та різними значеннями старшого коефіцієнта).
VII. Підсумки уроку
В якому з випадків правильно розв’язане рівняння?
А) 3х2 + 2х = 0, Х(3х + 2) = 0, Х = 0 або 3х + 2 = 0, Х = 0 або Відповідь. 0; | Б) 3х2 = 0, Х = 0. Відповідь. 0 | В) 3х2 + 2 = 0, 3х2 = 2,
Відповідь. |
VIII. Домашнє завдання
1. Вивчити схеми розв’язання неповних квадратних рівнянь.
2. Розв’язати неповні квадратні рівняння (різного рівня складності) за вивченими схемами.
3. Повторити схему розв’язання завдань на виділення повного квадрата двочлена.
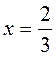 .
.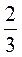
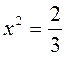 ,
, 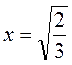 .
.