ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ
РОЗДІЛ 3 ТРИКУТНИКИ
& 12. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ
Якщо трикутники ABC і А1В1С1 дорівнюють один одному, то їх можна сумістити. При цьому якщо сумістяться вершини А і А1, В і В1, С і C1, то сумістяться й сторони: АВ з A1B1, ВС з В1С1, СА з C1A1 і кути: ∠A з ∠A1∠B з∠B1, ∠C, ∠C1. Отже, якщо ∆АВС =∆А1В1С1, то АВ = А1В1, ВС = В1С1, СА = С1А1, ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1.
Щоб довести, що дані трикутники рівні, необов’язково переконуватися в істинності всіх шістьох рівностей.
Теорема 10 (перша ознака рівності трикутників).
Якщо дві сторони і кут між
Доведений. Нехай АВС і A1B1C1 – два трикутники, у яких АВ = А1В1, АС = А1С1 і ∠A = ∠A1 (мал. 151). Доведемо, що ∆АВС = ∆А1В1С1.
Накладемо ∆A1B1C1 на ∆АВС так, щоб вершина А1 сумістилася з вершиною А, вершина В1 – з вершиною В, а сторона А1С1 наклалася на промінь АС. Це зробити можна, бо згідно з умовою A1B1 = АВ і ∠A1 = А. Оскільки А1С1 = АС, то при такому накладанні точка С1 суміститься з точкою С. У результаті всі вершини трикутника А1В1С1 сумістяться з відповідними вершинами трикутника ABC.
Отже, ∆A1B1C1 = ∆АВС.
Мал. 151
Теорема 11 (друга ознака рівності трикутників).
Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам іншого трикутника, то такі трикутники – рівні.
Доведення. Нехай ABC і А1В1С1 – два трикутники, у яких АВ = A1B1, ∠A = ∠A1 і ∠B = ∠B1 (мал. 152). Доведемо, що ∆АВС = А
∆А1В1С1, Накладемо ∆А1В1С1 на ∆АВС так, щоб вершина А1 сумістилася з вершиною А, вершина B1 – з вершиною В, а сторона А1С1 наклалася на промінь АС. Це зробити можна, бо АВ =А1В1 і ∠A = ∠A1. Оскільки ∠B =∠B1, то сторона B1C1 накладеться на промінь ВС. Отже, при такому накладанні промінь А1С1 суміститься з променем АС, а промінь В1С1 – з променем ВС. Точка C1, у якій перетинаються промені А1С1 і В1С1, суміститься з точкою С – точкою перетину променів АС і ВС. Як бачимо, трикутник А1В1С1 можна сумістити з трикутником ABC, а це означає, що ∆АВС = ∆A1В1C1.
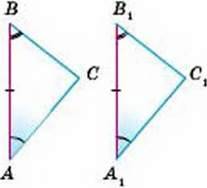
Мал. 152
Для допитливих
Існують ще й інші ознаки рівності трикутників (див. теорему 18).
На ознаки рівності трикутників згодом доведеться посилатися часто. Щоб не сплутати, яку з них названо першою, яку другою і т. д., їх краще розрізняти за змістом, говорити про ознаку рівності трикутників:
1) за двома сторонами і кутом між ними;
2) за стороною і двома прилеглими кутами:
3) за трьома сторонами (її доведемо пізніше).
Ці ознаки рівності трикутників називають загальними ознаками, бо вони правильні для будь-яких трикутників. Крім них, існують ще ознаки рівності прямокутних трикутників, рівнобедрених трикутників тощо.
Два рівносторонні трикутники рівні, якщо сторона одного з них дорівнює стороні іншого.
Спробуйте довести цю ознаку, користуючись загальними ознаками.
Запитання і завдання для самоконтролю
1. Сформулюйте першу ознаку рівності трикутників.
2. Сформулюйте другу ознаку рівності трикутників.
3. Доведіть ознаку рівності трикутників за двома сторонами і кутом між ними.
4. Доведіть ознаку рівності трикутників за стороною і прилеглими до неї кутами.
Виконаємо разом
1. Відрізки АВ і CD перетинаються в точці О так, що AO = DO і СО = ВО. Доведіть, що АС = BD.
– Розглянемо трикутники АСО і DBO (мал. 163). Їх кути при вершині О – вертикальні, отже, рівні. Відповідні сторони також рівні: AO = DО, СО = ВО. Згідно з першою ознакою рівності трикутників ∆АСО = ∆DBO. Сторони АС і BD цих трикутників відповідні, бо лежать проти рівних кутів при вершині О.
Отже, АС = BD.
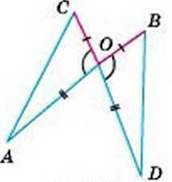
Мал. 153
2. Дві сторони трикутника дорівнюють одна одній. Доведіть, що медіани, проведені до цих сторін, також рівні.
– Нехай у трикутника AВC сторона АВ = АС, а ВК і СР – медіани (мал. 154).
АР = АХ як половини рівних сторін. ∆АВК = = ∆АСР, бо АВ = АС, АК = АР і ∠A – спільний. Отже, ВК = СР.
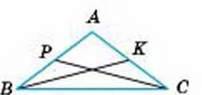
Мал. 154
ЗАДАЧІ І ВПРАВИ
Виконайте усно
351. Учні побудували в зошитах трикутники за двома сторонами 3 см і 5 см та кутом 60° між НИМИ. ЧИ рівні ці трикутники?
352. Учні побудували в зошитах трикутники за стороною 5 см і прилеглими до неї кутами 30° і 70°. Чи рівні ці трикутники?
353. Користуючись малюнком 155, доведіть:
А) якщо АВ = АD і ∠1 = ∠2, то ∆АВС = ∆АОС;
Б) якщо ∠1 = ∠2 і ∠B = ∠D, то ∆АBС = ∆АDС.
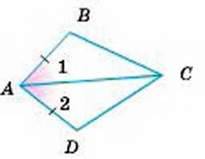
Мал. 155
354. Відрізки АВ і CD перетинаються в точці О так, що АО = ОВ і CO = OD. Доведіть, що ∆АОС = ∆BOD.
355. Відрізки KР і EF перетинаються в точці М так, що КМ – МР і EM = MF. Знайдіть відстань між точками К і E, якщо PF = 12 см.
356. На малюнку 156 АВ = CD, АВ | CD. Доведіть, що ∠AОВ = ∠COD.
357. Доведіть, що ∆АВС = ∆А1В1С1, якщо АС = А1С1, ∠A = ∠A1 і ∠B= ∠В1.
358. Нехай AM – медіана трикутника ABC і МК = МK (мал. 157). Доведіть, що ∆ACM = ∆КВМ.
359. У чотирикутнику ABCD АВ ‖ CD і ВС ‖ AD (мал. 158). Доведіть, що ∠B = ∠D.
Мал. 156
Мал. 157
Мал. 156
360. На бісектрисі кута А позначено точку D, на сторонах цього кута – точки В і С такі, що ∠BDA = ∠ADC. Доведіть, що BD = CD.
361. У рівносторонньому трикутнику ABC проведіть бісектрису AL і доведіть, що:
А) BL = LC;
Б) AL ⏊ ВС.
362. У чотирикутнику ABCD АВ ‖ CD і ВС ‖ AD. Проведіть відрізок BD і доведіть, що:
А) АВ = CD;
Б) BC = AD;
В) ∠A = ∠C.
363. Чи дорівнюють один одному трикутники, зображені на малюнку 159?
Мал. 159
364. Щоб виміряти на місцевості відстань між пунктами А і В, між якими не можна пройти (мал. 160), вибирають таку точку С, від якої можна пройти до А і до В. Потім на прямих АС і ВС відкладають відрізки СТ = АС і CP =DC. Відстань РТ дорівнює AВ. Чому?
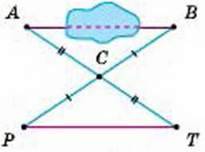
Мал. 150
365. Попередню задачу можна розв’язати іншим способом (мал. 161). Відкладають ∠BCM = ∠DCA і CM = СА. Тоді АВ = ВМ. Поясніть чому це так?
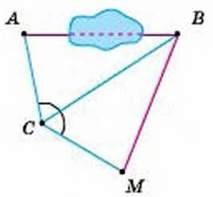
Мал. 161
366. Через кінці відрізка AВ проведено паралельні прямі АС і BD, а через середину О відрізка АВ – пряму, яка перетинає прямі АС і BD в точках С і D. Знайдіть відстань між точками А і С, якщо BD = 8 см.
367. Рівні відрізки АВ і CD перетинаються в точці О так, що ОА = ОС. Доведіть, що ∠АВС = ∠ADC і ∠BAD = ∠BCD.
368. Відрізки АВ і CD перетинаються в точці О, яка е серединою кожного з них. Доведіть, що АС і BD.
Б
369. Доведіть, що медіани рівних трикутників, проведені до рівних сторін, – рівні.
370. Доведіть, що в рівних трикутниках рівні відповідні:
А) бісектриси; б) висоти.
371. Усі сторони шестикутника ABCDEF рівні i всі його кути рівні (мал. 162). Доведіть, що трикутник АСЕ – рівносторонній.
372. На малюнку 163 AD = CF, ∠1 = ∠2 і ∠3 = ∠4. Доведіть, що ∆АВС = ∆DEF.
373. Бісектриса AL трикутника ABC перпендикулярна до сторони ВС. Доведіть, що АВ = АС.
374. Щоб знайти відстань між пунктами А та X (мал. 164), на березі річки позначили точки В і С так, щоб виконувались рівності ∠1 = ∠2 і ∠3 = ∠4. Шукана відстань АХ дорівнює відстані АС. Чому?
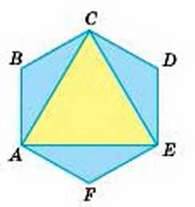
Мал. 162
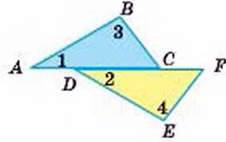
Мал. 163
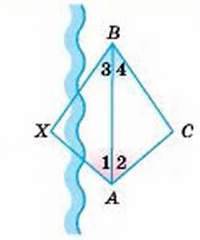
Мал. 164
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
375. Один із двох кутів на 40й більший за інший. Знайдіть ці кути, якщо суміжні а ними кути відносяться як 7 : 5.
376. Чи має трикутник рівні сторони, якщо дві його сторони відносяться як 5 : 4, третя – на 1 см більша за їх півсуму, а периметр трикутника дорівнює 28 см?
377. Чому дорівнює кут між бісектрисами внутрішнього і зовнішнього кутів трикутника, взятих при одній вершині?
378. Скількома способами можна розрізати прямокутник на два рівні прямокутники? А на дві рівні фігури?
379. Як два рівні квадрати розрізати на рівні частини і скласти з них один квадрат?
Геометрія навколо нас

Самостійна робота 3
Варіант 1
1. Накресліть гострокутний трикутник і проведіть його медіани.
2. Два кути трикутника дорівнюють 35° і 68°. Знайдіть третій кут.
3. Периметр трикутника дорівнює З5 см. Знайдіть довжини йога сторін, якщо одна з них довша за другу на 3 см і коротша від третьої на 5 см.
4. У трикутнику ABC сторони АВ і ВС – рівні, а ВН – бісектриса. Доведіть, що ∆АВН = ∆СВН.
Варіант 2
1. Накресліть прямокутний трикутник і проведіть його бісектриси.
2. Два кути трикутника дорівнюють 110° і 67°. Знайдіть третій кут.
3. Знайдіть довжини сторін трикутника, якщо одна з них довша за другу на 8 м, а за третю – на 5 м, а периметр трикутника дорівнює 50 м.
4. У трикутнику КРТ висота РМ є водночас і бісектрисою. Доведіть, що ∆КРМ = ∆ТРМ.
Варіант З
1. Накресліть тупокутний трикутник і проведіть його медіани.
2. Два кути трикутника дорівнюють 87° і 56°. Знайдіть третій кут.
3. Периметр трикутника дорівнює 62 см. З найдіть довжини йога сторін, якщо одна з них довша за другу в 2 рази, а за третю – на 8 см.
4. У трикутнику ABC кути А і С – рівні, а ВМ – висота. Доведіть, що ∆АВМ = ∆СВМ.
Варіант 4
1. Накресліть довільний трикутник і проведіть усі йога висоти.
2. Два кути трикутника дорівнюють 130° і 25°. Знайдіть третій кут.
3. Периметр трикутника дорівнює 85 м. Знайдіть довжини йога сторін, якщо одна з них коротша від другої у 2 рази, а від третьої – на 1 м.
4. У трикутнику КРТ висота PH є водночас і медіаною. Доведіть, що ∆КРН = ∆ТРН.
ЗАДАЧІ ЗА ГОТОВИМИ МАЛЮНКАМИ
А
1
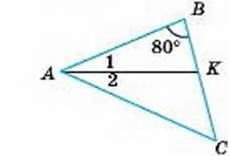
∠A =  ∠C
∠C
∠A, ∠C
2
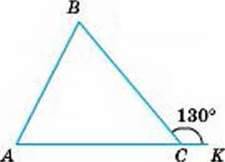
∠B і ∠C = 4 : 6.
∠B, ∠C
3
∠1 = 30°,
∠2 = 40°.
∠3, ∠4
4
∠A = ∠C, ∠1 = ∠2.
∠AKC
Б
1
∠B = ∠А.
∠A, ∠B
2
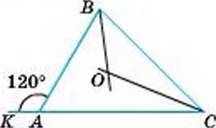
ВО, СО – бісектриси.
∠BOC.
3
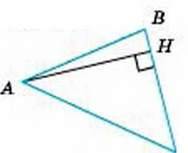
∠CAB = ∠C = 50°.
∠BAH, ∠CAН
4
AO, BO – бісектриси.
∠С
Запитання і завдання для самоконтролю
1. Що таке трикутник?
2. Назвіть елементи трикутника.
3. Наведіть приклади предметів довкілля, що мають форму рівних геометричних фігур.
4. Якими бувають трикутники?
5. Сформулюйте означення прямокутного трикутника.
6. Сформулюйте означення тупокутного трикутника.
7. Сформулюйте означення гострокутного трикутника.
8. Що таке висота трикутника?
9. Сформулюйте означення медіани трикутника.
10. Що таке бісектриса трикутника?
11. Чим відрізняється бісектриса трикутника від бісектриси кутя?
12. Сформулюйте теорему про суму кутів трикутника.
13. Доведіть теорему про суму кутів трикутника.
14. Що таке зовнішній кут трикутника?
15. Сформулюйте теорему про зовнішній кут трикутника.
16. Доведіть теорему про зовнішній кут трикутника.
17. Чи правильно, що зовнішній кут трикутника більший за кожний внутрішній кут, не суміжний з ним?
18. Чому дорівнює сума кутів чотирикутника?
19. Які фігури називають рівними?
20. Яким знаком відношення позначають рівність фігур?
21. Наведіть приклади предметів довкілля, що мають форму рівних геометричних фігур.
22. Сформулюйте властивості рівності фігур.
23. Які трикутники називають рівними?
24. Сформулюйте ознаку рівності двох кіл.
25. Сформулюйте першу ознаку рівності трикутників.
26. Сформулюйте другу ознаку рівності трикутників.
27. Сформулюйте і доведіть ознаку рівності рівносторонніх трикутників.
28. Доведіть ознаку рівності трикутників за двома сторонами і кутом між ними.
29. Доведіть ознаку рівності трикутників за стороною і прилеглими до неї кутами.
Тестові завдання 3
1. Один із кутів трикутника дорівнює 40°, а другий – на 20° більший. Третій кут трикутника дорівнює: | А) 100°; б) 80°; В) 60°; г) 120°. |
2. Зовнішні кути трикутника дорівнюють 100° і 120°. Знайдіть внутрішній кут при третій вершині. | А) 60°; б) 90°; В) 40°; г) 80°. |
3. Кути трикутника пропорційні числам 2, 3 і 5. Знайдіть найменший кут трикутника. | А) 30°; б) 64°; В) 28°; г) 36°. |
4. ∆ABC = ∆А1В1С. Який знак слід поставити замість * в записі: АА * АА1? | А) <; б) =; В) >; г) ≠. |
5. ∆АВС = ∆A1B1C1. Який знак слід поставити замість * в записі: АВ * A1B1? | А) <; б) >; В) =; г) ≠. |
В. ∆АВС = ∆А1В1C1, АВ = 5 см, АС = 7 см. Знайдіть ВС, якщо Р∆А1В1С1 = 21см. | А) 11см; б) 19 см; В) 10см; г)9см. |
7. ∆АВС = ∆А1В1С1, ∠А = 70°, ∠В = 60°. Знайдіть ∠C1. | А) 50°; б) 90°; В) 30°; г) 70°. |
Для виконання завдань 8-10 скористайтесь умовою: відрізки АВ і CD перетинаються в точці О так, що АО = ВО і CO = DO. | |
8. Який трикутник дорівнює трикутнику АОС? | А) ∆АОD; б) ∆BOD; В) ∆СОВ; г) ∆CBD. |
9. Якому куту дорівнює кут ОАС? | A) ∠ODB; б) ∠OBD; В) ∠BOD; г)∠AOD. |
10. Яке твердження хибне? | А) АС = BD; Б) АС ‖ BD; В) АВ ‖ CD; Г) АО = ОВ. |
ТИПОВІ ЗАДАЧІ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ
1. Намалюйте довільний трикутник і проведіть до його більшої сторони медіану, бісектрису, висоту.
2. Два кути трикутника дорівнюють 96° і 43°. Знайдіть міру третього кута трикутника.
3. Знайдіть кути трикутника АВС, якщо він дорівнює трикутнику КРТ, у якого ∠К = 70°, ∠Р = 50°.
4. Знайдіть периметр трикутника KLM, якщо ∆KLM = ∆ABC і АВ = 5 см, ВС = 3 см, АС = 4 см.
5. ВК – висота трикутника ABC. Знайдіть АС, якщо АК = 5 см, КС= 11см, ∠A = 120°.
6. Відрізки AS і КР перетинаються в точці О так, що ОА = OB, ОК = ОР. Доведіть, що ∆АОР = ∆ВОК.
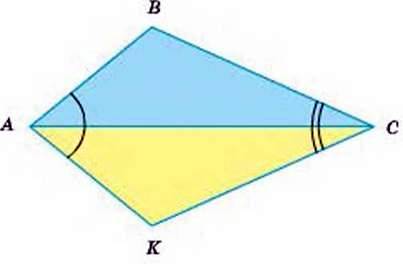
7. Зображені на малюнку 165 трикутники ABC і АКС такі, що ∠BAC = ∠КАС І ∠ВСА = ∠КСА. Доведіть, що АВ = АК.
Мал. 165
8. Знайдіть куги трикутника, якщо його зовнішні куги пропорційні числам 3, 7 і 8.
9. У трикутнику ABC проведено висоти АР і ВН. Доведіть, що АР = ВН, якщо PC = НС
10. У трикутнику ABC проведено медіани АР і ВН. Доведіть, що ∆АРС = ∆ВНС, якщо АС = SC.