Головна ⇒ 📌Довідник з математики ⇒ Парність функції
Парність функції
Математика – Алгебра
Числові функції
Парність функції
Функція називається Парною, якщо:
1)  ;
;
2)  .
.
У парних функцій протилежним значенням аргументу відповідають рівні значення функції.
Графік парної функції симетричний відносно осі Oy.
Функція називається Непарною, якщо:
1)  ;
;
2)  .
.
У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції.
Графік непарної функції
Приклади
1)
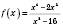 ;
; 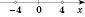
– симетрична відносно нуля.
(На координатній прямій 0 позначено для того, щоб простежити, чи симетрична
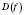 відносно 0.)
відносно 0.)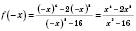 .
.Функція парна.
2)
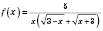 ;
;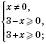
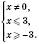
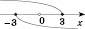
– симетрична відносно 0.
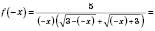
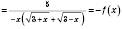 .
.Функція непарна.
3)
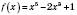 .
.– симетрична
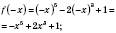
;
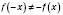 .
.Функція не є ані парною, ані непарною.
4)
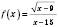 .
.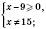
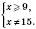
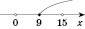
– несиметрична відносно нуля.
Функція не є ані парною, ані непарною.
Related posts:
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...
- Числові функції. Зростаючі і спадні, парні і непарні функції УРОК 1 Тема. Числові функції. Зростаючі і спадні, парні і непарні функції Мета уроку: Узагальнення і систематизація знань учнів про числові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції). І. Мотивація навчання Процеси реального світу тісно пов’язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв’язок […]...
- Функції Урок № 68 Тема. Функції Мета: виявити рівень засвоєння обов’язкових знань та вмінь з теми “Функція”, передбачених програмою з математики та ступінь сформованості навичок. Тип уроку: контроль знань та вмінь. Форма проведення: тематична контрольна робота. Хід уроку І. Перевірка домашнього завдання II. Умова тематичної контрольної роботи Варіант 1 Варіант 2 1?. Функцію задано формулою У […]...
- Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Урок № 85 Тема. Повторення та систематизація знань та вмінь учнів з теми “Функції і графіки” Мета: повторити та систематизувати набуті учнями знання про зміст основних понять теми та види задач; повторити та систематизувати основні способи дій, що були опановані учнями під час вивчення теми; провести підготовку до підсумкового тематичного оцінювання. Тип уроку: повторення та […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ ФУНКЦІЇ Цілі: – навчальна: сформувати поняття функції, аргументу та значення функції; домогтися засвоєння способів задання функції; сформувати вміння розв’язувати задачі, які передбачають застосування цих понять; – розвивальна: формувати культуру усного та писемного мовлення; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, працьовитість; Тип уроку : засвоєння нових знань, […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції УРОК № 19 Тема. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Функції Математика – Алгебра Функції Функціональною відповідністю, або Функцією, називають таку відповідність між двома змінними, коли кожному значенню однієї змінної відповідає одне значення другої змінної. Першу змінну називають Незалежною, або Аргументом функції, а другу – Залежною, або Функцією від першої змінної. Усі значення, які приймає незалежна змінна, утворюють Область визначення функції. Записують: , де x – […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Графік функції Урок № 63 Тема. Графік функції Мета: формувати вміння виконувати побудову графіка функції, заданої формулою “по точках”; відпрацьовувати навички “читання” графіків функцій; провести діагностику засвоєння матеріалу з теми “Функція. Графік функції”. Хід уроку I. Організаційний момент Вступне слово вчителя. Перевірка готовності учнів до уроку; місце уроку в темі, план роботи на уроці. II. Перевірка домашнього […]...
- Функція. Область визначення та область значень функції Урок № 61 Тема. Функція. Область визначення та область значень функції Мета: вдосконалювати та поглиблювати вміння та навички розв’язувати основні види завдань для функції, заданої формулою. Тип уроку: застосування знань. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання 1) № 1,2 перевіряємо, зібравши зошити, № 2 бажано розібрати (навести приклади і сформулювати основну ідею, […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Степенева функція УРОК 41 Тема. Степенева функція Мета уроку. Познайомити учнів із степеневою функцією, її властивостями і графіками. І. Перевірка домашнього завдання 1. Перевірити наявність виконаного домашнього завдання. 2. Розв’язування вправ. А) Обчислити . Відповідь: 5. Б) Спростити вираз . Відповідь: ab. В) Спростити вираз . Відповідь: 2a. II. Сприймання і усвідомлення матеріалу про степеневу функцію Степеневою […]...
- Функція. Область визначення функції. Область значень функції Урок № 60 Тема. Функція. Область визначення функції. Область значень функції Мета: закріпити термінологію, відпрацювати навички роботи з поняттями функції; відпрацювати навички роботи із функцією, заданою формулою і таблично; знаходити функції аргументу, області визначення функції. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (традиційно) II. Перевірка домашнього завдання @ Оскільки основна частина […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- ПОВТОРЕННЯ. ФУНКЦІЇ Цілі: – навчальна: узагальнити та систематизувати знання учнів про зміст основних понять теми “Функції”; – розвивальна: формувати вміння аналізувати й узагальнювати інформацію, бачити закономірності; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати відповідальність за результати своєї роботи, наполегливість у досягненні мети, віру у власні сили; Тип уроку : узагальнення та систематизація знань. Обладнання та наочність: […]...