Переміщення й координата під час прямолінійного рівноприскореного руху
1-й семестр
МЕХАНІКА
1. Кінематика
Урок 9/11
Тема. Переміщення й координата під час прямолінійного рівноприскореного руху
Мета уроку: навчити учнів розв’язувати задачі на обчислення переміщення пройденого шляху в разі прямолінійного рівноприскореного руху
Тип уроку: вивчення нового матеріалу
План уроку
Контроль знань | 5 хв. | 1. Що називають прискоренням? 2. Який рух називають рівноприскореним? 3. Швидкість у разі прямолінійного рівноприскореного |
Вивчення нового матеріалу | 25 хв. | 1. Переміщення в разі прямолінійного рівноприскореного руху. 2. Рівняння координати в разі прямолінійного рівноприскореного руху. 3. Середня швидкість у разі прямолінійного рівноприскореного руху. 4. Співвідношення між переміщенням і швидкістю в разі прямолінійного рівноприскореного руху |
Закріплення вивченого матеріалу | 15 хв. | 1. Тренуємося розв’язувати задачі. 2. Контрольні запитання |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Переміщення в разі прямолінійного рівноприскореного руху
Щоб
У випадку рівномірного руху проекція sx чисельно дорівнює площі фігури, обмеженої графіком 
X(t) і віссю Ot, тобто sx = Xt.
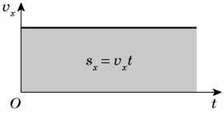
Це дієво й під час нерівномірного руху, оскільки час руху можна розбити на такі малі інтервали часу, упродовж яких рух тіла можна вважати практично рівномірним.
Якщо початкова швидкість тіла не дорівнює нулю, то фігура, обмежена графіком X(t) і віссю Ot, – трапеція, що складається з прямокутника площею 0xt і трикутника площею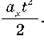 
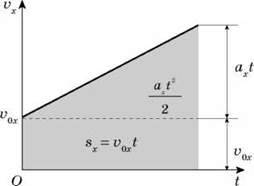
Отже, у разі прямолінійного рівноприскореного руху з початковою швидкістю проекція переміщення обчислюється за формулою:
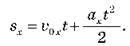
У випадку прямолінійного рівноприскореного руху без початкової швидкості проекція переміщення обчислюється за формулою:
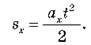
Площу трапеції можна обчислити і як добуток півсум основ (0x і X) на висоту (t). Отже,
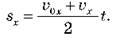
2. Рівняння координати в разі прямолінійного рівноприскореного руху
Оскільки x = x0 + sx, дістаємо:
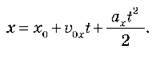
3. Середня швидкість у разі прямолінійного рівноприскореного руху
Проекція середньої швидкості визначається, як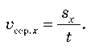 
Скориставшись формулою 
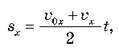маємо, що в разі рівноприскореного руху проекція середньої швидкості дорівнює середньому арифметичному проекції початкової та кінцевої швидкостей:
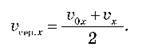
4. Співвідношення між переміщенням і швидкістю в разі прямолінійного рівноприскореного руху
Для обчислення переміщення можна отримати формулу, до якої не входить час руху.
З виразу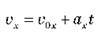 
отримуємо час 
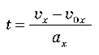підставляємо у формулу 
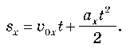Тоді дістаємо:
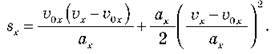
Звідси:
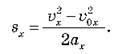
Якщо початкова швидкість дорівнює нулю, то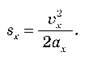 
Проекція швидкості дорівнює:
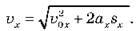
Запитання до учнів під час викладу нового матеріалу
1. Яким є геометричний зміст переміщення?
2. Як за графіком швидкості визначити проекцію переміщення?
3. Чому дорівнює середня швидкість у разі прямолінійного рівноприскореного руху?
4. Як пов’язані переміщення і швидкість у випадку прямолінійного рівноприскореного руху?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Тренуємося розв’язувати задачі
1. Потяг починає рух зі стану спокою й рухається рівноприскорено. На першому кілометрі шляху його швидкість зростає до 10 м/с. Наскільки вона зросте на другому кілометрі?
Розв’язування
З формули шляху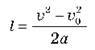 
випливає, що швидкість потяга після проходження першого кілометра дорівнює:
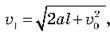
А після проходження другого кілометра (коли пройдений шлях дорівнює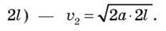 
Тоді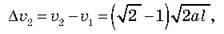 
тобто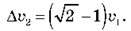 
Отже, ?2 = 4,1 м/с.
2. За який час автомобіль, рухаючись зі стану спокою з прискоренням 0,5 м/с2, пройде шлях 100 м?
3. Автомобіль почав рух із прискоренням 0,5 м/с2 у той момент, коли повз нього рівноприскорено проїжджав трамвай зі швидкістю 18 км/год. Яку швидкість матиме автомобіль, коли наздожене трамвай? Прискорення трамвая – 0,3 м/с2.
4. Куля, що летіла зі швидкістю 400 м/с, пробила стіну завтовшки 20 см, у результаті чого її швидкість зменшилася до 100 м/с. Скільки часу рухалася куля в стіні?
5. Потяг почав гальмувати за швидкості 72 км/год. Якою буде його швидкість після проходження двох третин гальмового шляху?
2). Контрольні запитання
1. Як розв’язується основна задача механіки у випадку прямолінійного рівноприскореного руху?
2. Що являє собою в разі прямолінійного рівноприскореного руху графік залежності переміщення від часу? графік координати?
3. Як залежить шлях від часу в разі прямолінійного рівноприскореного руху?
Що ми дізналися на уроці
– Проекція переміщення в разі прямолінійного рівноприскореного руху з початковою швидкістю:
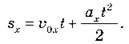
– Проекція переміщення в разі прямолінійного рівноприскореного руху без початкової швидкості:
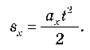
– Рівняння координати в разі прямолінійного рівноприскореного руху:
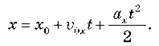
– Середня швидкість у випадку прямолінійного рівноприскореного руху:
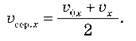
– Співвідношення між переміщенням і швидкістю:
– з початковою швидкістю: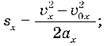 
– без початкової швидкості: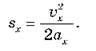 
– Проекція швидкості в разі прямолінійного рівноприскореного руху:
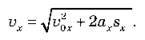
Домашнє завдання
1. П.: § 10
2. 36.:
Р1) – 4.17; 4.18; 4.19;4.20;
Р2) – 4.29; 4.31; 4.33, 4.36;
Р3) – 4.65, 4.66; 4.73; 4.76.
(1 votes, average: 5.00 out of 5)
Loading...