Перетворення цілих виразів
Цікаві вправи
Тема. Перетворення цілих виразів
1. Ігрові моменти.
А) За 1 хвилину записати якомога більше таких двочленів, щоб у разі винесення спільного множника за дужки в дужках залишилось 2х – 3;
Б) За 1 хвилину записати якомога більше таких дробів із знаменником х(х – 2), які можна скоротити.
В) За 1 хвилину придумайте якомога більше таких дробів, щоб після їх скорочення утвори вся дріб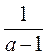 
.
Г) Грають парами. У кожного з партнерів по 5-7 карток. На кожній із карток написано або одночлен, або двочлен. Перший
Потім партнери міняються ролями.
Д) Учитель. Я задумав алгебраїчний дріб, і ви зможете відгадати його. Один з учнів записує на дошці будь-який дріб (для зручності будемо використовувати букву х), а я знайду добуток цих дробів і запишу його.
Наприклад, учень записав дріб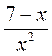 
; 
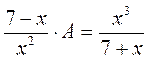. Який дріб я задумав?
2. Сума двох дробів з однаковими знаменниками дорівнює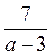 
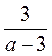. Які ці дроби?3. Замість квадратиків запишіть такі одночлени, щоб рівність стала тотожністю: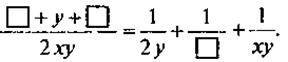 
4. Знайдіть два одночлени, якщо їх добуток дорівнює (ab)12, а частка дорівнює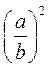 
.
5. Замість * поставте такі знаки дій, щоб рівність стала тотожністю (можна використовувати дужки):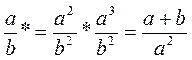 
.
Тема. Квадратні корені
1. Дано 4 числа: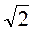 
; 
; 
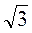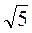і 
. І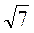з них складають різні частки, наприклад 
; 
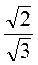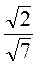І т. д.
1) Скільки таких часток можна скласти?
2) Знайдіть найменшу та найбільшу частку.
3) Чому дорівнює добуток усіх часток?
2. 1) Запишіть число 2 рівно двома двійками, використовуючи відомі дії (можна дужки).
2) Запишіть 6 разів число 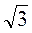і знаки дій, щоб утворилось число 6.
3) Використовуючи 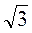і 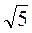по 2 рази, утворіть число 2.
3. Що більше: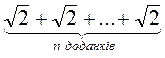 
чи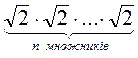 
?
4. Придумайте такі два числа а і b, щоб одночасно виконувались три умови:
А)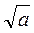 
і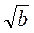 
– ірраціональні числа;
Б) 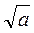– –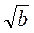 натуральне число;
В)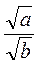 
– раціональне число.
5. Замість х і у назвіть такі натуральні числа, щоб виконувалась нерівність 6 < х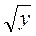
< 7.
6. Ігровий момент.
На дошці записані 24 натуральні чиста: 2, 3, 4, …, 23, 24, 25. Учень має назвати весь ряд за такими правилами: показуючи послідовно на число 2, говорить 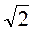і т. д. Якщо корінь здобувається, то учень називає значення кореня. Якщо це число складене, то слід подати його у вигляді добутку коренів. Наприклад, 4 = 2; 6 = 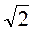–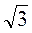, тобто під знаком кореня мають бути тільки прості числа.
Хто зможе назвати весь ряд без помилки?
7. Десять секунд на роздуми.
На розв’язування кожного з наступних завдань спробуйте витрати ти не більше 10 секунд.
1) 
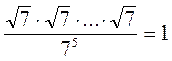. Скільки множників у чисельнику?
2) Що більше: А чи В, якщо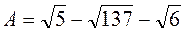 
, 
?
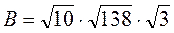3) Чому дорівнює а, якщо 10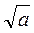= а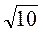
?
4) Обчисліть: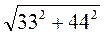 
.
8. Ігровий момент. Грають парами. Перший записує число виду а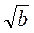, де а і b – натуральні числа, менші від 15, наприклад 7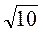. Другий має записати число виду 
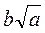, тобто 10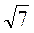. Потім числа порівнюються. Перемагає той, у кого число вийшло більше. Потім обмінюються ролями
9. Ігровий момент.
Грають двоє. Кожний записує по одному додатному числу на аркуші паперу. Потім перший знаходить середнє арифметичне цих чисел, а другий знаходить добуток і добуває квадратний корінь із добутку. Чи можна передбачити, хто пер може в цій грі?
(1 votes, average: 5.00 out of 5)
Loading...