Перетворення коренів
УРОК 34
Тема. Перетворення коренів
Мета уроку. Познайомити учнів з найпростішими перетвореннями радикалів: винесення множника за знак радикала; внесення множника під знак радикала; зведення радикалів до найпростішого (нормального) вигляду; ознайомлення з поняттям подібних радикалів.
І. Перевірка домашнього завдання
1. Фронтальна бесіда за № 1-12, 17-24 із “Запитання і завдання для повторення до розділу III.
2. Виконання вправ № 9, 19 до розділу III.
II. Сприймання і усвідомлення матеріалу про винесення множника за знак радикала
Вивчені властивості коренів дають змогу виконувати перетворення коренів.
1. Винесення множника з під знака радикала.
В деяких випадках підкореневий вираз розкладається на множники так, що із одного чи декількох із них можна добути точний корінь. Добувши корені із цих множників, одержані числа можна записати перед знаком кореня. Таке перетворення називається винесенням множника за знак радикала.
Наприклад:
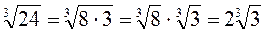 ;
; 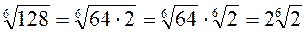 ;
;
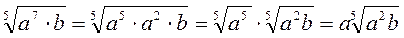 ;
;
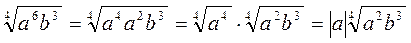 .
.
Взагалі, якщо a 
 0, то
0, то 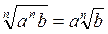 .
.Якщо a – довільне, то 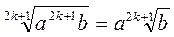 ;
; 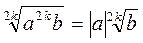 .
.
Виконання вправ
1. Винесіть множники за знак радикала:
А) 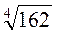 ; б)
; б) 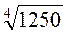 ; в)
; в) 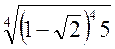 ; г)
; г) 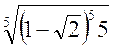 .
.
Відповідь: а) 3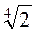 ; б) 5
; б) 5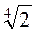 ; в) (
; в) (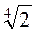 – 1)
– 1) 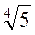 ; г) (1 –
; г) (1 – 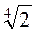 )
) 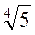 .
.
2. Винесіть множники за знак кореня, якщо а > 0, b > 0:
А) 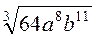 ; б)
; б) 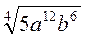 ; в)
; в) 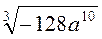 ; г)
; г) 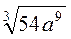 .
.
Відповідь: а) 4a2b3 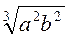 ; б) a3b
; б) a3b 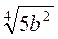 ; в) – 4a3
; в) – 4a3 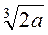 ; г) 3a3
; г) 3a3 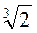 .
.
3. Винесіть множники за знак кореня:
А) 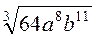 ; б)
; б) 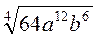 ; в)
; в) 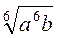 ; г)
; г) 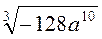 .
.
Відповідь: а) 4a2b3 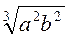 ; б) 2|а|3|b|
; б) 2|а|3|b|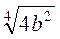 ; в) |а|
; в) |а|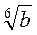 ; г) – 4a3
; г) – 4a3 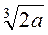 .
.
2. Внесення множника під знак кореня.
Перетворення, обернене до винесення множника за знак кореня, називається внесенням множника під знак кореня.
Наприклад: 2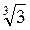 =
= 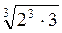 =
= 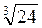 ; 3
; 3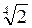 =
= 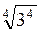 –
– 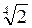 =
= 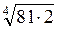 =
= 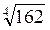 ;
;
A 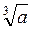 =
= 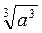 –
– 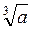 =
= 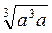 =
= 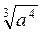 , якщо а > 0;
, якщо а > 0;
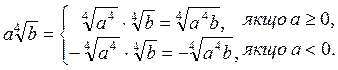
Взагалі:
 0, то а
0, то а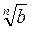 =
= 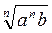 .
.2) Якщо а – довільне, то 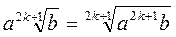 ;
;
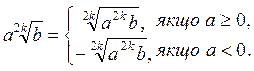
1. Внесіть множник під знак кореня:
А) 3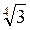 ; б) -2
; б) -2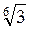 ; в) (1 –
; в) (1 –  )
)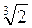 ; г) (1 –
; г) (1 –  )
)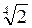 .
.
Відповідь: а) 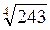 ; б) –
; б) – 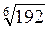 ; в)
; в) 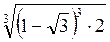 ; г) –
; г) – 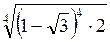 .
.
2. Внесіть множники під знак кореня, якщо а > 0, b > 0:
А) – b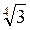 ; б) аb
; б) аb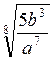 ; в) а
; в) а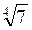 ; г) – аb
; г) – аb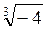 .
.
Відповідь: а) –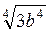 ; б)
; б) 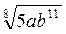 ; в)
; в) 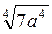 ; г)
; г) 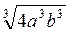 .
.
3. Внесіть множники під знак кореня:
А) а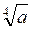 ; б) а
; б) а ; в) – аb
; в) – аb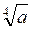 .
.
Відповідь: а) 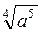 ; б)
; б) 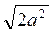 , якщо а
, якщо а  0, –
0, – 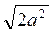 , якщо а < 0; в) –
, якщо а < 0; в) –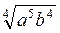 , якщо b
, якщо b  0,
0, 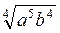 , якщо b < 0.
, якщо b < 0.
III. Сприймання і усвідомлення зведення радикалів до найпростішого вигляду, поняття подібних радикалів
Будемо вважати, що радикал приведено до простішого вигляду, якщо: підкореневий вираз не містить дробів; раціональні множники винесено за знак кореня, показник кореня і показник степеня підкореневого виразу скорочено на їхній найбільший спільний множник.
Приклад. Приведемо радикали до простішого вигляду:
1) 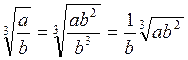 ; 2)
; 2) 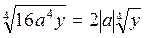 .
.
Радикали називаються подібними, якщо після приведення їх до простішого вигляду вони мають рівні підкореневі вирази і однакові показники.
Наприклад, подібними є радикали: а) 3 ;а
;а ;
;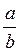
 ; б) 5
; б) 5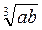 ;
;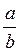
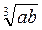 ; (а-1)
; (а-1)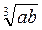 .
.
Раціональний множник, який стоїть перед знаком радикала, називається коефіцієнтом. Наприклад, 3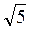 . У цьому виразі 3 є коефіцієнтом.
. У цьому виразі 3 є коефіцієнтом.
Щоб стверджувати, що радикали подібні чи ні, їх треба привести до простішого вигляду.
Наприклад, 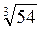 і
і 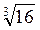 подібні, оскільки
подібні, оскільки 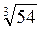 =
=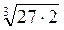 =3
=3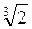 , а
, а 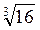 =
=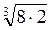 =2
=2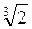 .
.
IV. Підведення підсумків уроку
V. Домашнє завдання
Розділ III § 1 (3; 4). Запитання і завдання для повторення розділу III. № 25-37. Вправи № 28, 33 (1-3), 48 (1-3).