Перетворення звичайних дробів у десяткові і навпаки
Урок № 3 5
Тема. Перетворення звичайних дробів у десяткові і навпаки
Мета: повторити й систематизувати знання, які учні мають з 5 класу про перетворення десяткових дробів у звичайні і навпаки; доповнити ці відомості уявленням про нескінченні періодичні дроби та ознакою дробу, що його можна записати скінченним десятковим дробом; сформувати вміння записувати дробове число у вигляді десяткового (періодичного) дробу.
Тип уроку: систематизація і узагальнення знань учнів.
Хід уроку
І. Актуалізація опорних знань
Усні вправи
1.
6 : 10 | 0,2 – 4 | 5 + 0,8 | 0,76 – 0,3 |
0,8 : 2 | 2,1 -3 | 0,23 + 7 | 2,54 – 2 |
2,1 : 7 | 0,7 – 10 | 0,48 + 0,2 | 0,82 – 0,02 |
0,5 : 10 | 0,5 – 2 | 0,6 + 0, 34 | 0,63 – 0,6 |
4,1 : 2 | 0,25 – 4 | 2,7 + 1,12 | 0,8 – 0,25 |
2. Серед виразів знайдіть рівні: 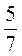 ; 3:8; 7:5;
; 3:8; 7:5; 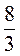 ;
; 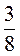 ; 5:7.
; 5:7.
3. Виконайте ділення: 3:4; 7:20.
4. Розкладіть на прості множники числа: 4; 6; 8; 15; 20.
II.
@ Після виконання усних вправ учні повторюють відомості, які вони здобули у 5 класі, а саме:
1) звичайний дріб 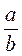 Означає ділення а і b;
Означає ділення а і b;
2) щоб звичайний дріб 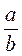 записати десятковим дробом, можна а : b.
записати десятковим дробом, можна а : b.
III. Доповнення знань. Мотивація навчальної діяльності
Задача. Обчисліть значення виразу 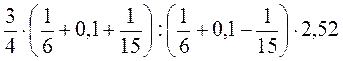 .
.
Аналізуємо ситуацію і бачимо, що маємо як десяткові, так і звичайні дроби, тому привести їх треба до одного вигляду, але, розпочавши перетворення, бачимо, що 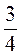 = 0,75, але
= 0,75, але 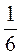 = 0,1666…
= 0,1666…
Тому виникають запитання:
1) Що це за дроби (0,1666… і подібні), як вони називаються і як їх записують?
2) Що робити у випадку, коли у виразі є десяткові і звичайні дроби?
@ Подальше викладення матеріалу уроку ведеться традиційно за планом.
1. Уявлення про нескінченний періодичний дріб. Поняття періоду десяткового дробу. Запис періодичних дробів у “скороченій формі”.
2. Ознака нескоротного дробу, який можна записати нескінченними десятковими дробами.
IV. Засвоєння вмінь
Усні вправи
1. Прочитати дроби: 0,3; 1,(5); 1,(57); 1,5(7).
2. Скінченним чи нескінченним періодичним десятковим дробом запишеться такий дріб: 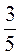 ;
; 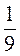 ;
; 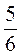 ;
; 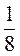 ;
; 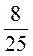 ;
; 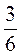 ?
?
Письмові вправи
II, III рівні
1. Запишіть десятковим дробом: 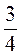 ;
; 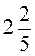 ;
; 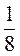 ;
; 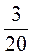 ;
; 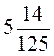 ;
;  ;
; 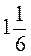 ;
; 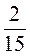 ;
; 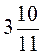 ;
; 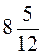 ;
; 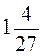 .
.
Спочатку перевіряємо, якого вигляду десятковий дріб ми дістаємо (скінченний чи нескінченний), потім для нескінченного виконуємо ділення, допоки не встановимо період.
2. Виконайте дії в десяткових дробах: а) 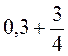 ; б)
; б) 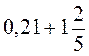 ; в)
; в) 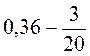 ; г)
; г) 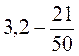 .
.
3. Знайдіть середнє арифметичне чисел: а) 3,25 і 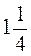 ; б)
; б) 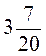 ;
; 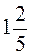 і 4,15; в) 10;
і 4,15; в) 10; 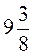 і 15,005.
і 15,005.
4. Довжина прямокутника 3,6 дм, а ширина – на 1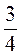 дм менша. Знайдіть ширину прямокутника.
дм менша. Знайдіть ширину прямокутника.
5. Швидкість катера у стоячій воді 22,5 км/год, швидкість течії річки 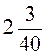 км/год. Знайдіть швидкості катера за течією річки і проти течії. (Задачі, що передбачають дії з десятковими та звичайними дробами)
км/год. Знайдіть швидкості катера за течією річки і проти течії. (Задачі, що передбачають дії з десятковими та звичайними дробами)
Додаткові вправи
1. Обчисліть значення виразу:
А) 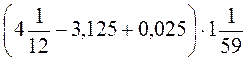 ; б)
; б) 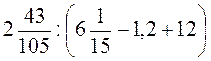 ; в)
; в) 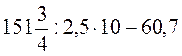 .
.
2. Спростіть вираз, використавши властивості дій, та обчисліть його значення:
А) 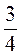 А + 0,6а + 4
А + 0,6а + 4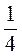 А – 0,1а; а = 0; 1; 4;
А – 0,1а; а = 0; 1; 4; 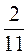 .
.
Б) 10 + 3,4b + 8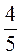 B – 2,26; b = 0; 1; 9; 0,1.
B – 2,26; b = 0; 1; 9; 0,1.
3. Яке число більше і на скільки:
А) 10 % якою становлять 8 або 12 % якого становлять 24;
Б) 24 % якого становлять 72 або 12 % якого становлять 60?
V. Підсумки уроку
В яких дробах краще обчислювати значення виразу:
А) 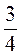 + 0,25; б)
+ 0,25; б)  + 0,25; в)
+ 0,25; в) 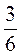 + 0,25?
+ 0,25?
VI. Домашнє завдання
1. Виконайте дії в десяткових дробах: а) 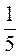 – 0,15; б) 3
– 0,15; б) 3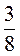 + 2,125; в) 5,4 –
+ 2,125; в) 5,4 – 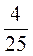 ; г)
; г) 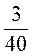 + 2,03.
+ 2,03.
2. Швидкість катера за течією річки 24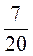 км/год, швидкість течії 2,2 км/год. Знайдіть швидкість катера у стоячій воді та проти течії річки.
км/год, швидкість течії 2,2 км/год. Знайдіть швидкість катера у стоячій воді та проти течії річки.
3. За першу годину автомобіль проїхав 48 км, за другу – 43,2 км, а за третю – 44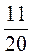 км. Знайдіть середню швидкість автомобіля за ці 3 години.
км. Знайдіть середню швидкість автомобіля за ці 3 години.
4. У спортивних секціях займається 20 учнів 6-А класу, що становить – усіх учнів класу. Скільки учнів у цьому класі?