Головна ⇒ 📌Довідник з математики ⇒ Періодичність тригонометричних функцій
Періодичність тригонометричних функцій
Математика – Алгебра
Тригонометричні функції
Періодичність тригонометричних функцій
Функція 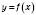 називається Періодичною з періодом
називається Періодичною з періодом 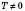 , якщо для будь-якого x з області визначення функції числа
, якщо для будь-якого x з області визначення функції числа 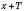 і
і 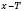 також належать області визначення й виконується умова:
також належать області визначення й виконується умова: 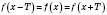 .
.
Якщо T – період функції 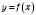 , то всі числа виду nT, де
, то всі числа виду nT, де 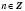 ,
,  ,
,
Щоб побудувати графік періодичної функції з періодом T, достатньо побудувати графік на відрізку завдовжки T, а потім зробити паралельне перенесення одержаного графіка на відстані nT вправо і вліво вздовж осі Ox
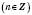 .
.Тригонометричні функції є періодичними. Найменшим додатним періодом функцій
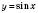 і
і 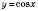 є
є 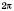 . Найменшим додатним періодом функцій
. Найменшим додатним періодом функцій 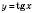 і
і 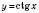 є число
є число  .
.Отже:
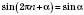 ;
; 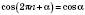
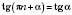 ;
; 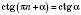 .
.Теорема. Якщо функція
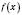 є періодичною і має період T, то функція
є періодичною і має період T, то функція 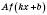 , де A, k, b – деякі числа, а
, де A, k, b – деякі числа, а 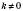 , теж є періодичною, період її дорівнює
, теж є періодичною, період її дорівнює 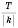 .
.Так, періодом функції
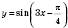 є число
є число 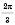 , періодом функції
, періодом функції 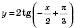 є число
є число 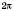 .
.Властивості тригонометричних функцій та їх графіків
Related posts:
- Періодичність тригонометричних функцій УРОК 8 Тема. Періодичність тригонометричних функцій Мета уроку: Введення поняття періодичної функції; знаходження найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій У = sin (kx + b), у = cos (kx + b), У = tg (kx + b), у = ctg (kx + b). І. Перевірка домашнього завдання 1. Побудуйте на одиничному […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
- Властивості тригонометричних функцій УРОК 10 Тема. Властивості тригонометричних функцій Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакопостійності; найбільші і найменші значення). І. Перевірка домашнього завдання Перевірити правильність побудови графіків […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Урок № 58 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60°. Розв’язування задач Мета: закріпити знання учнями змісту формул доповнення та числових значень тригонометричних функцій кутів 30°, 45°, 60°. Сформувати вміння застосовувати формули до розв’язування задач. Тип уроку: застосування знань, умінь та навичок. Наочність та обладнання: конспект 22. Хід уроку I. Організаційний етап […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій УРОК 3 Тема. Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій Мета уроку: Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = […]...
- Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- ОБЛАСТЬ ВИЗНАЧЕННЯ ТА ОБЛАСТЬ ЗНАЧЕНЬ ФУНКЦІЇ Цілі: – навчальна: удосконалити знання означень області визначення та області значень функції; удосконалити вміння знаходити область визначення та область значень функції; – розвивальна: формувати вміння міркувати за аналогією; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, працьовитість, дисциплінованість; Тип уроку : удосконалення знань, умінь і навичок. Обладнання та наочність: Хід уроку […]...
- Парність функції Математика – Алгебра Числові функції Парність функції Функція називається Парною, якщо: 1) ; 2) . У парних функцій протилежним значенням аргументу відповідають рівні значення функції. Графік парної функції симетричний відносно осі Oy. Функція називається Непарною, якщо: 1) ; 2) . У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції. Графік непарної функції симетричний відносно […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Логарифмічна функція, її графік і властивості УРОК 56 Тема. Логарифмічна функція, її графік і властивості Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправ № 13, 15, 20. 2. Розв’язування вправ, аналогічних домашнім. А) Обчисліть: ; . =====–=. ====–= 5. Б) Обчисліть . ==== 52 – 3-2 = 25 […]...
- Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 54 Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації Мета: – формувати теоретичну базу знань учнів з теми, спираючись на міжпредметні зв’язки; – розвивати практичні вміння та навички щодо опрацювання табличної інформації за допомогою формул та вбудованих […]...