Перпендикуляр і похила
Геометрія
Стереометрія
Перпендикуляр і похила
Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину.
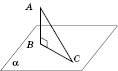
На рисунку AB – перпендикуляр; AC – похила; BC – проекція.
Відстанню від прямої до паралельної
Відстанню між паралельними площинами називається відстань від будь-якої точки однієї площини до другої площини.
Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини. Кінець відрізка, що лежить у площині, називається Основою похилої.
Відрізок, який сполучає основи перпендикуляра й похилої, проведених з однієї і тієї самої точки, називається Проекцією похилої.
Властивості похилих, проведених з однієї точки до однієї
1. Похилі, проведені до площини з однієї точки (рисунок нижче зліва), рівні тоді й тільки тоді, коли вони мають рівні проекції.
2. Якщо з точки до площини проведені дві похилі, то більша та з них, яка має більшу проекцію, і навпаки, більша похила має більшу проекцію.
Зверніть увагу, що ці властивості зберігаються для похилих, які проведені до площини з різних точок, але мають однакову довжину перпендикуляра (рисунок справа).
Related posts:
- Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Урок 31 Тема. Перпендикуляр і похила. Взаємозв’язок між довжинами похилих, проведених з однієї точки, і довжинами їх проекцій Мета уроку: формування понять: перпендикуляр до площини, похила, основа похилої, основа перпендикуляра, проекції похилої на площину, відстань від точки до площини. Виявлення взаємозв’язку між довжинами двох похилих, проведених з однієї точки до площини, і довжинами їх проекцій. […]...
- Перпендикуляр і похила. Розв’язування задач Урок № 36 Тема. Перпендикуляр і похила. Розв’язування задач Мета: сформувати в учнів свідоме розуміння змісту понять похилої до прямої, проекції похилої на пряму, а також властивостей перпендикуляра, похилих та їх проекцій. Сформувати вміння: – відтворювати зміст вивчених понять; – знаходити названі геометричні об’єкти на рисунку; – виконувати рисунок із зображенням названих об’єктів за даним […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...
- Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі УРОК № 53 Тема. Взаємне розміщення прямої та площини і площин у просторі. Перпендикуляр до площини. Взаємне розміщення площин у просторі Мета уроку: повторити, привести в систему й розширити відомості про площину та взаємне розміщення двох площин у просторі; ознайомити учнів з різними випадками взаємного розміщення прямої і площини; дати уявлення про перпендикуляр до площини. […]...
- ПОХИЛА ПЛОЩИНА – ПРОСТІ МЕХАНІЗМИ Фізика підготовка до ЗНО комплексне видання МЕХАНІКА 3. ЗАКОНИ ЗБЕРЕЖЕННЯ В МЕХАНІЦІ 3.8. ПРОСТІ МЕХАНІЗМИ 3.8.3. ПОХИЛА ПЛОЩИНА Щоб тіло, яке перебуває на похилій площині, було в стані спокою і рівномірного (без тертя) руху, необхідно прикласти силу, паралельну похилій площині і в стільки ж разів меншу від сили тяжіння, у скільки разів висота похилої площини […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Перпендикулярність прямих і площин Геометрія Стереометрія Перпендикулярність прямих і площин Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у […]...
- Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Урок 35 Тема. Відстань від точки до прямої. Розв’язування задач на застосування теореми про три перпендикуляри Мета уроку: формування вмінь учнів застосувати теорему про три перпендикуляри до розв’язування задач, знаходження відстані від точки до прямої. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання. 1. Два учні відтворюють на дошці розв’язування задач № 13, 41. […]...
- Куля Геометрія Тіла обертання Куля Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, […]...
- Поворот Геометрія Рух Поворот Поворотом площини навколо даної точки називається такий рух, при якому кожний промінь, що виходить із даної точки, повертається на один і той самий кут в одному й тому самому напрямку (див. рисунок)....
- Перпендикулярність площин Геометрія Стереометрія Перпендикулярність площин Дві площини, що перетинаються, називаються Перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих двох площин, перетинає їх по перпендикулярних прямих (див. рисунок). Будь-яка площина, перпендикулярна до прямої перетину перпендикулярних площин, перетинає їх по перпендикулярних прямих. Ознака перпендикулярності площин Теорема 1. Якщо площина проходить через пряму, перпендикулярну до другої площини, то […]...
- Властивість точки, рівновіддаленої від сторін многокутника Урок 36 Тема. Властивість точки, рівновіддаленої від сторін многокутника Мета уроку: формування вмінь учнів застосовувати властивість ортогональної проекції точки, рівновіддаленої від сторін многокутника, до розв’язування задач. Обладнання: стереометричний набір, схема “Коло, вписане в многокутник” Хід уроку 1. Перевірити правильність виконання вправ № 42, 48, 53 за записами, зробленими на дошці до початку уроку. Нехай ABCD […]...
- Блоки. Похила площина 1-й семестр МЕХАНІЧНІ ЯВИЩА 2. Взаємодія тіл Урок 11/24 Тема. Блоки. Похила площина Мета уроку: познайомити учнів із застосуванням правила моментів для блоків як різновидів важеля; познайомити учнів з одним з видів простих механізмів – похилою площиною. Тип уроку: урок вивчення нового матеріалу. План уроку Контроль знань 5 хв. 1. Які перетворення сили відбуваються в […]...
- Конус Геометрія Тіла обертання Конус Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса. Конус називається Прямим (далі просто “конус”), якщо […]...
- Перетворення симетрії в просторі. Симетрія в природі і на практиці Урок 47 Тема. Перетворення симетрії в просторі. Симетрія в природі і на практиці Мета уроку: формування знань учнів про перетворення симетрії в просторі та застосування знань до розв’язування задач. Обладнання: схема “Перетворення фігур”. Хід уроку І. Перевірка домашнього завдання 1. Усне коментування розв’язування домашніх завдань. 2. Математичний диктант. Дано трикутник АВС: Варіант 1 – А […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Відстань між мимобіжними прямими Геометрія Стереометрія Відстань між мимобіжними прямими Спільним перпендикуляром до двох мимобіжних прямих називається відрізок із кінцями на цих прямих, перпендикулярний до кожної з них. Теорема. Дві мимобіжні прямі мають спільний перпендикуляр, і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. Відстанню між мимобіжними прямими називається довжина […]...
- Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої Розділ 2. Взаємне розміщення прямих па площині § 7. Перпендикулярні прямі. Перпендикуляр. Відстань від точки до прямої 128. m ⊥ n, MN ⊥ АВ. 129. KA ⊥ c, ВМ ⊥ с. 130. ВL ⊥ a. MВ ⊥ a. 131. 1) Відрізки AB і MN перпендикулярні, оскільки вони лежать на перпендикулярних прямих a і b. 2) […]...
- Побудова перпендикулярних прямих і площин Урок 29 Тема. Побудова перпендикулярних прямих і площин Мета уроку: формування вмінь учнів будувати перпендикулярні прямі і площини. Обладнання: стереометричний набір. Хід уроку 1. Перевірити правильність виконання задачі № 8 за записами (з пропусками), зробленими на дошці до початку уроку. Нехай у трикутнику АВС (C = 90°) АС = … , ВС = … , […]...
- Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...
- Розв’язування задач на знаходження відстані між мимобіжними прямими Урок 41 Тема. Розв’язування задач на знаходження відстані між мимобіжними прямими Мета уроку: формування вмінь учнів у знаходженні відстані між двома мимобіжними прямими. Обладнання: стереометричний набір, моделі куба і прямокутного паралелепіпеда. Хід уроку 1. Фронтальна бесіда за контрольними запитаннями № 13-15 та перевірка правильності розв’язання домашньої задачі. 2. Математичний диктант. Дано зображення куба: варіант 1 […]...
- Теорема про триперпендикуляри Геометрія Стереометрія Теорема про триперпендикуляри Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої. Приклади застосування теореми про три перпендикуляри 1. На рисунку – куб. , тому […]...
- Симетрія відносно прямої Геометрія Рух Симетрія відносно прямої Нехай а – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр AX на пряму а. На продовженні цього перпендикуляра за точку А відкладемо відрізок . Точка називається Симетричною точці X відносно прямої А. Якщо точка X лежить на прямій а, то вона симетрична сама собі відносно прямої а. Очевидно, […]...
- Симетрія відносно точки УРОК № 34 Тема. Симетрія відносно точки Мета уроку: формування поняття симетрії відносно точки; вивчення властивостей симетрії відносно точки; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують симетрію відносно точки; будують фігури, у які переходять дані […]...
- Переміщення – Кінематика 5. Механіка 5.1. Кінематика 5.1.9. Переміщення Переміщення – спрямований відрізок прямої, який сполучає початкове положення тіла (матеріальної точки) з його наступним положенням. Позначається буквою s. Одиниця вимірювання – один метр (1 м). Переміщення – векторна величина....
- Відстань між мимобіжними прямими Урок 40 Тема. Відстань між мимобіжними прямими Мета уроку: формування понять спільного перпендикуляра, відстані між мимобіжними прямими. Обладнання: стереометричний набір. Хід уроку 1. Фронтальне опитування. 1) Які дві площини називаються перпендикулярними? 2) Сформулюйте ознаку перпендикулярності площин. 3) Як розташована пряма, яка лежить в одній із двох перпендикулярних площин і перпендикулярна до лінії перетину цих площин, […]...
- Геометричне місце точок Урок № 47 Тема. Геометричне місце точок Мета: – сформувати в учнів уявлення про зміст поняття “геометричне місце точок”, властивість і ознаку точок, що належать ГМТ ; – сформувати знання змісту та схеми доведення теореми про ГМТ. Сформувати вміння: – відтворювати означення властивості та ознаки ГМТ, теорем про ГМТ; – використовувати ці твердження під час […]...
- Поняття про перетворення фігур УРОК № 32 Тема. Поняття про перетворення фігур Мета уроку: дати уявлення учням про перетворення фігур на площині. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: пояснює, що таке перетворення. Хід уроку І. Перевірка домашнього завдання Перевірити наявність виконаного домашнього завдання та відповісти на запитання, які виникли […]...