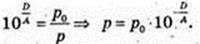Показникова та логарифмічна функції
1.
Обчисліть:
1) 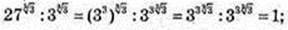
2) 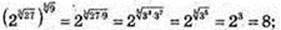
3) 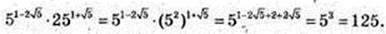
2.
Спростіть вираз:
1) 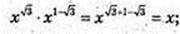
2) 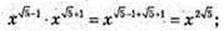
3) 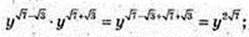
4) 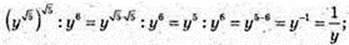
5) 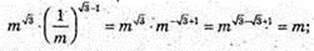
6) 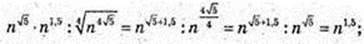
7) 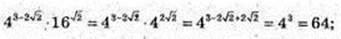
8) 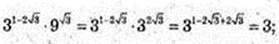
9) 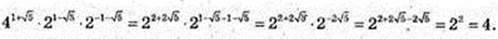
3.
Послуговуючись калькулятором, обчисліть з точністю до 0,01:
23,14 ≈ 8,82
23,15 ≈ 8,88
23,141 ≈ 8,82
23,142 ≈ 8,83
4.
Послуговуючись
5.
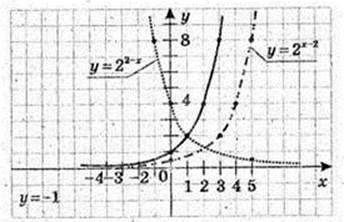
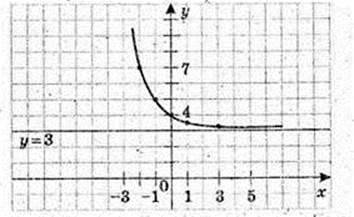
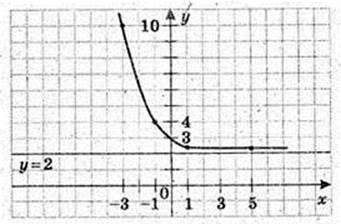
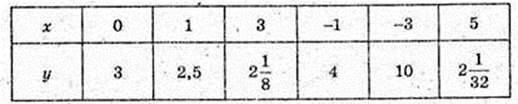
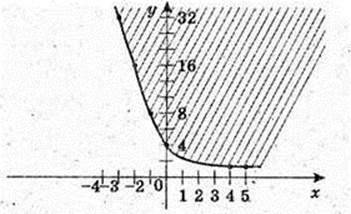
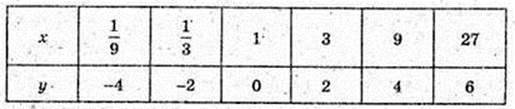
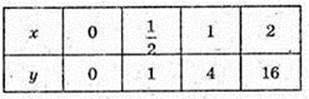
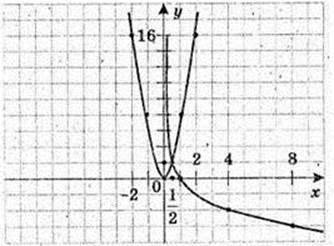
Використавши графік функції у = 2х знайдіть наближено:
1) значення функції в точках 1,5 і (-1,5):
21,5 ≈ 4,2-1,5 ≈ 0,6;
2) значення аргументу, при яких значення функції дорівнює 0,4:
Х – ? 2х = 0, х ≈ – 0,7;
3) абсцису точки його перетину з прямою у = 1,5;
Х – ? 2х = 1,5, х ≈ 0,4.
6.
Користуючись графіком функції у = 2х, побудуйте графіки функцій:
1) у = 2х-2, у > 0;
2) у = 22-х, у > 0;
3)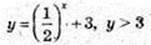
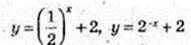
4) у = 2х – 1, у > -1
5) у = 2 |х|, у ≥ 1
Графік симетричний відносно осі Оу.
6) 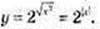 (Графік дивись п. 5).
(Графік дивись п. 5).
7.
1) Область визначення функції у = 32х – 1-, х? (-∞; +∞),
Область значень функції у > -1, у? (-1; +∞);
2) у = 1
Область визначення функції х? (-∞; +∞).
Множина значень – одна точка у = 1;
3) 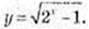
Х – ? 2х -1 ≥ 0, 2х ≥ 1, х ≥ 0
Область визначення функції х? [0; +∞).
Множина значень функції у? [0; +∞).
8.
У = 3х-1, х? [2; 4].
Найменше значення функції на проміжку [2; 4] дорівнює 3, якщо х = 2,
Найбільше значення функції дорівнює 27, якщо х = 4;
2)у = 2х-1, х? [-1; 2].
Найменше значення функції на проміжку [-1; 2] дорівнює 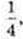 якщо х = 2;
якщо х = 2;
Найбільше значення дорівнює 2, якщо х = -1;
3) у = 31- 2x, х? [-1; 1].
Найбільше значення функції на проміжку [-1; 1] дорівнює 27, в точці х = -1;
Найменше значення функції дорівнює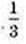 в точці х = 1;
в точці х = 1;
4) 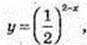 х? [-2; 2]; y = 2x-2.
х? [-2; 2]; y = 2x-2.
Найбільше значення функції на проміжку [-2; 2] дорівнює 1 в точці x = -2; найменше значення дорівнює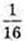 в точці х = -2.
в точці х = -2.
9.
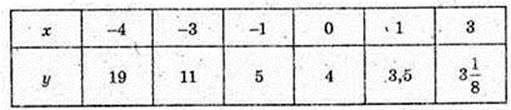
У = 0,3 ×- (1,5)2x – 1 = 0,45
1) х? [-3; 3] t = 0,5
X | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 |
Y | -0,432 | -0,424 | -0,410 | -0,391 | -0,361 | -0,317 | -0,25 |
X | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | |
Y | -0,15 | 0 | 0,225 | 0,563 | 1,07 | 1,83 |
2)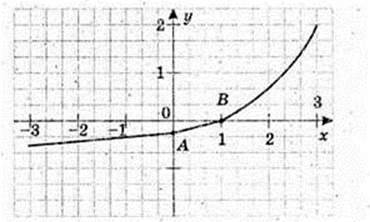
3) А(0; -0,25), B(1; 0);
4) х? (-∞; 0].
10.
ν = 2,5 × (1 – 2,7 -1,5t)
1) t1 = 10 с, v(10) = 2,5 × (1 – 2,7-15) = 2,50 м/с;
T2 = 20 с, v(20) = 2,5 × (1 – 2,7-30) = 2,5 м/с;
V(0) = 2,5 × (1 – 2,70) = 0;
2) v(0) = 0, v(10) – v(0) = 2,50 м/с;
V(20) – v(10) = 0,00 м/с.
11.
1) v = 2,5 × (1 – 2,71,5t) t = 10 с, v = 2,5 × (1 – 2,7-15)
12.
1) x – ? 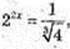
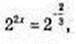
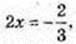
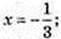
2) x – ? 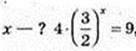
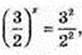
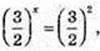 x = 2;
x = 2;
3) 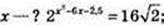
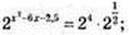
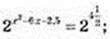
Х2 – 6х – 2,5 = 4,5; х2 – 6х – 7 = 0; х1 = -1; х2 = 7.
13.
1) х – ? (0,5)x > 1, х < 0, x? (-∞; 0);
2) х – ? 3x < 9; 3x < 32, х? (-∞; 2);
3) 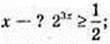 23x ≥ 2-1; 3х ≥> -1;
23x ≥ 2-1; 3х ≥> -1; 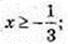
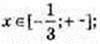
4) 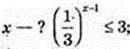 3-x+1 ≤ 31; – х + 1 ≤ 1; – х ≤ 0; х ≥ 0 х? [0; +∞).
3-x+1 ≤ 31; – х + 1 ≤ 1; – х ≤ 0; х ≥ 0 х? [0; +∞).
14.
1) f(х) = (2х + 2-2х)2 – (2x – 2 -2x)2 = (2х + 2-2x + 2х – 2-2х) × (2х + 2 -2х – 2x + 2-2х) =
= 2 × 2x × 2 × 2-2x = 22 × 2x × 2-2x = 22+x-2x = 22-x; f(х) = 2-x+2;
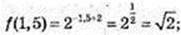 f(1) = 2-1 + 2 = 21; f(-1) = 21+2 = 23 = 8;
f(1) = 2-1 + 2 = 21; f(-1) = 21+2 = 23 = 8;
3) вісь у має вид х = 0, f(0) = 4. А(0; 4); вісь x має вид у = 0, 2-x + 2 ≠ 0,
Графік функції не перетинає вісь х; 2-х + 2= 21; – х + 2 = 1, x= 1. В(1; 2);
4) Область визначення функції у = 2-x +2, x? (-∞; +∞),
Множина значень функції, у? (0; +∞)

5) Найбільше значення функції у = 2 – х + 2,на проміжку [-1; 2] дорівнює 21+ 2 = 8 в точці х = -1; найменше значення функції на проміжку [-1; 2] дорівнює 2-2+2 = 20 = 1 в точці х = 2;
6) x – ? 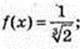
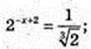
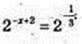
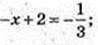
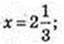
Х – ? 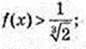
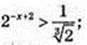
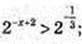
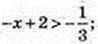
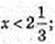
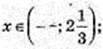
7) x -? 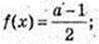 2 – x+2 = (а -1) × 2 -1.
2 – x+2 = (а -1) × 2 -1.
А ≤ 1 розв’язків не існує; а > 1, розв’язки існують, а? (1; +∞);
8) у = -3 f(2х – 1); y = -3 × 3-(2x-1)+2 = -3 × 2-2x+4; у = -3 × 2-2х+4, у? (-∞; 0).
15.
F(х)=(3x + 3-2x)2 – (3х – 3-2x)2 – 3-x
1) f(х) = (3х + 3-2х + 3х – 3-2x) × (3х + 3-2x – 3х + 3-2x) – 3-х = 2 × 3х × 2 × 3-2х – 3-х =
= 4 × 3х-2x – 3-x = 4 × 3-x – 3-х = 3 × 3-х = 3-х+1, F(х) = 3-х+1.
2) 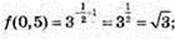
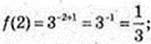 f(-2) = 3-(-2)+1 = 32+1 = 33 = 27;
f(-2) = 3-(-2)+1 = 32+1 = 33 = 27;
3) х =- 0, y(0) = 30+1 = 3; A(0; 3).
У = 0, 3-x+1 ≠ 0 не існує точок перетину графіка функції з віссю х.
Х – ? 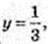
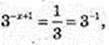 -х + 1 = -1, х = 2;
-х + 1 = -1, х = 2; 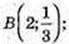
4) Область визначення функції f(х) = 3-x+1, х? (-∞: +∞).
Множина значень функції у? (0; +∞).
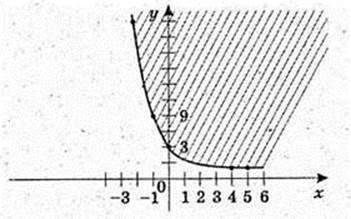

5) х? [-2; 1], yнайб.= 27 при х = -2; yнайм. = 1 при х = 1.
6) х -? 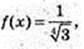
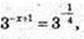
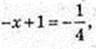
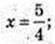
Х -? 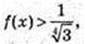
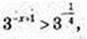
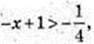
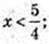
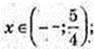
7) а-? 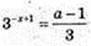 існує розв’язок цього рівняння?
існує розв’язок цього рівняння?
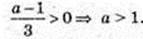 а? (1; +∞);
а? (1; +∞);
8) f(х) = -2f(-х) + 1 = -2 × 3-9-x+1) + 1 = -2 × 3x + 1. f(x) < 1.
Множина значень функції(-∞; 1).
16.
1) 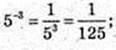
2) 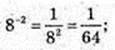
3) 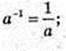
4) 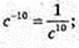
5) 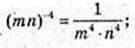
6) 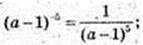
7) 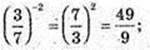
8) 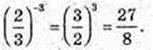
17.
1) 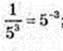
2) 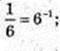
3) 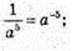
4) 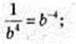
5) 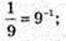
6) 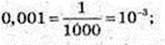
7) 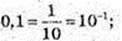
8) 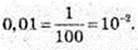
18.
1) 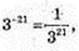
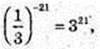
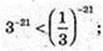
2) 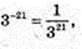
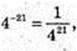 3-21 > 4-21;
3-21 > 4-21;
3) 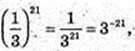
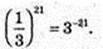
19.
1) 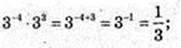
2)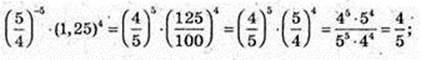
3)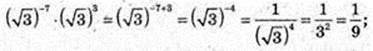
4)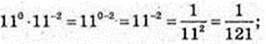
5)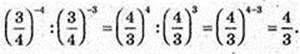
20.
1) log216 = log224 = 4 × log22 = 4 × 1 = 4;
2) log2 1 = 0;
3)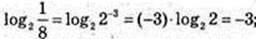
4)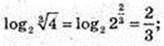
5)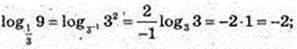
6)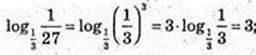
7)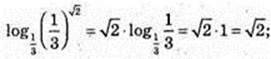
8)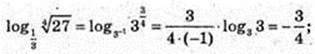
9)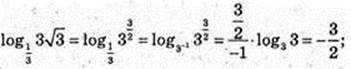
10)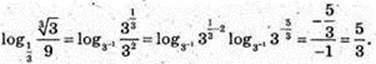
21.
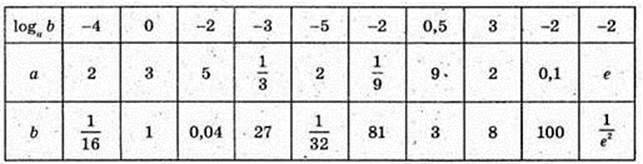
22.
1) 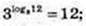
2) 10lg3 = 3;
3) eln5 = 5;
4) 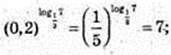
5) 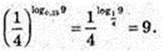
23.
1) 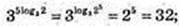
2) 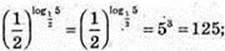
3) 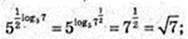
4) 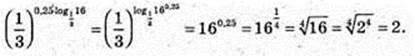
24.
1) 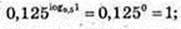
2) 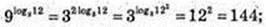
3) 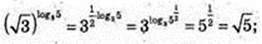
4) 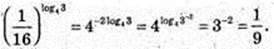
25.
1) x – ? logx3 = 2,x2 = 3, 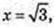 x > 0; О. Д.3.
x > 0; О. Д.3. 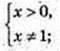
2) x -? 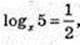
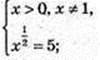 Х = 52 = 25;
Х = 52 = 25;
3) x -? 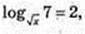
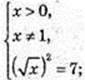 х = 7;
х = 7;
4) x -? 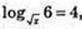
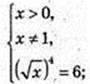
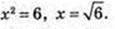
26.
1) log6 x = 3, 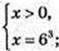 x = 216;
x = 216;
2) log2(5 – х) = 3, 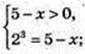 x = 5 – 23 = 5 – 8 = -3, x = -3;
x = 5 – 23 = 5 – 8 = -3, x = -3;
3) log3(x + 2) = 3, 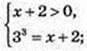 x = -2 + 33 = -2 + 27 = 25, x = 25;
x = -2 + 33 = -2 + 27 = 25, x = 25;
4) 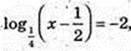
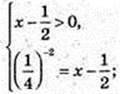
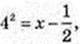
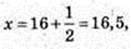 х= 16,5.
х= 16,5.
27.
1) log3 2,7 + log310 = log3 2,7 × 10 = log3 27 = 3;
2) 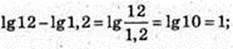
3) logа а5 = 5, якщо а > 0, а ≠ 1;
4) 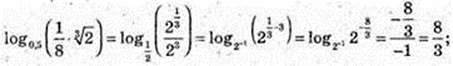
5) 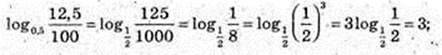
6) 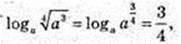 якщо а > 0, а ≠ 1.
якщо а > 0, а ≠ 1.
28.
1) 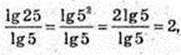 або
або 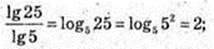
2) 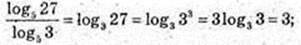
3) 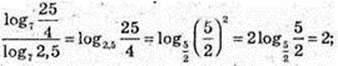
4) 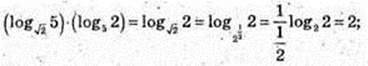
5) 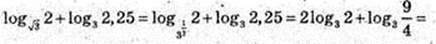
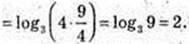
29.
1) lg 17 ≈ 1,23;
2) lg 127 ≈ 2,10;
3) ln 2,9 ≈ 1,06;
4) ln 0,72 ≈ -0,329;
5) log3 12 ≈ 3,402;
6) log025 6,2 ≈ -1,316.
30.
1) х – ? 2x = 5, х= log2 5 ≈ 2,322;
2) х – ? 1,2x = 4, x = log1,2 4 ≈ 7,604;
3) х – ? 1 + е0,25x = 5, е0,2x = 4,
0,2x = ln 4, х = 5 ln 4 ≈ 6,931;
4) х – ? 23х-1 = 5, 3х – 1 = log 2 5;
3х = 1 + log2 5 = log2 2 + Іog25 = log210;
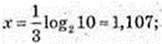
5) х – ?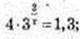
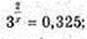
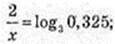
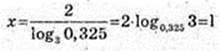
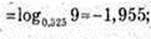
6) х – ? 3×2-2 = 2; x2 -2 = Іоg3 2;
Х2 = 2 + log3 2 = log3 9 + log3 2 = Іоg318;
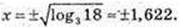
31.
1) х – ? 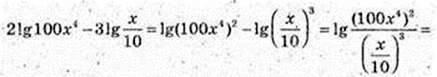
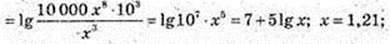
Тоді 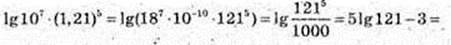
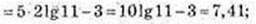
2) 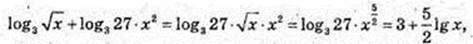
Х = 1,21, тоді 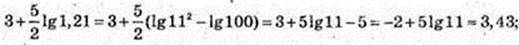
3) 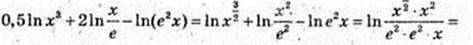
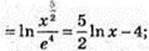
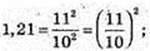
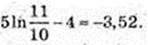
32.
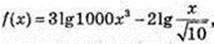
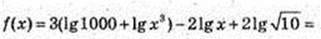
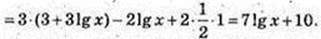
1) f(x) = 7 lg x + 10;
2) х = 0,01; f(0,01) = 7 × lg 0,01 + 10 = -7 × 2 + 10 = -14 + 10 = -4;
X = 1,2; f(1,2) = 7 lg 1,2 + 10 ≈ 10,55;
3) x -? 7 lgx + 10 = 3, 7 lg x = -7, lgx = -1, x = 0,1.
33.
V = 2,5 × (1 – 2,7-1,5t)
1) t – ? 2,5 × (1 – 2,7-1,5t) = 2,2;
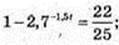
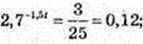
-1,5t = log2,7 0,12; t ≈ 1,42 c;
2) t – ? 0,95 × 2,5 = 2,5 × (1 – 2,7-1,5t);
1 – 2,7-1,5t = 0,95; 0,05 = 2,7-1,5t;
-1,5t = log2,70,05; t ≈ 2,01c,
34.
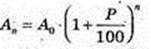
X – ? 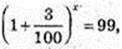
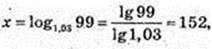 x = 152.
x = 152.
35.
X -? 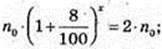 (1,08)x = 2;
(1,08)x = 2; 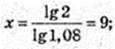 x = 9.
x = 9.
36.
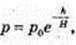 h – ?
h – ?
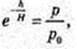
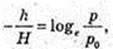
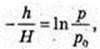
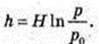
37.
1) f(x) = log3(x + 3), x + 3 > 0, x? (-3; +∞);
2) f(x) = lg(x2 + 1), x? (-∞;+∞);
3) f(x) = log0,2(1 – x2), x – x2 > 0, x2 < 1, |x| < 1, x? (-1; 1);
4) f(x) = lg(2x – 1), 2x – 1 > 0, 2x > 1, x > 0, x? (0; +∞);
5) 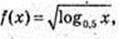
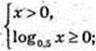 0 < x < 1, x? (0; 1];
0 < x < 1, x? (0; 1];
6) f(x) = alogx, x > 0, x? (0;+ ∞)
7) f(x) = lg(lg x), lg x > 0, x > 0, x? (1; +∞).
38.
1) log5 3 > 0;
2) log3 0,9 < 0;.
3) log0,7 8 < 0;
4) log0,3 0,6 > 0.
39.
1) 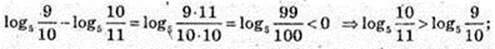
2) 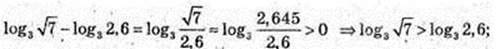
3) 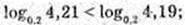
4) 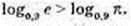
40.
1) a = 2-0,5; 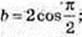 c = Iog0,1 2;
c = Iog0,1 2; 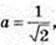 b = 0, c = Iog0,1 2 < 0, c < b < a;
b = 0, c = Iog0,1 2 < 0, c < b < a;
2) 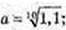
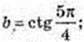 c = Iog25;
c = Iog25; 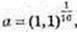 b = -1, c = Iog2 5 > 2 ,b < a < c.
b = -1, c = Iog2 5 > 2 ,b < a < c.
41.
1) log5 x > log5 3, x > 3, x? (3; +∞);
2) 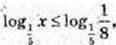
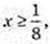
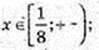
3) Iog3 x < Iog3 2, 0 < x < 2, x? (0; 2);
4) 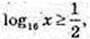
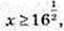
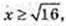 x > 4, x? [4; +∞);
x > 4, x? [4; +∞);
5) Iog9 х2 > 1, x2 > 9, |x| > 3, x? (-∞; 3) 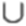 (3; +∞);
(3; +∞);
6) 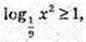
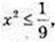
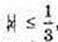 x ≠ 0,
x ≠ 0, 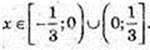
42.
1) x – ? 2log2x = x, x > 0, x ∞ (-∞; 0) 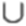 (0; +∞)
(0; +∞)
2) х – ? 10lgx2 = x2, x2 = х2; x2 ≠ 0, х? (-∞; 0) 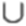 (0; +∞);
(0; +∞);
3) x – ? Iogx2 3 = 0,5 Iog|x|3; 2Iogx2 3 = Iog|x|3; 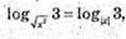 |х| ≠ 1, х ≠ 0.
|х| ≠ 1, х ≠ 0.
X? (-∞; 1) 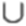 (-1; 0)
(-1; 0) 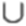 (0; 1)
(0; 1) 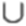 (1; +∞);
(1; +∞);
4) х – ? 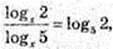 x > 0, x ≠ 1. x? (0; 1)
x > 0, x ≠ 1. x? (0; 1) 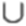 (1; +∞).
(1; +∞).
43.
1) 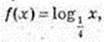 x? [1; 4].
x? [1; 4].
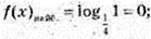
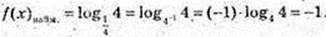
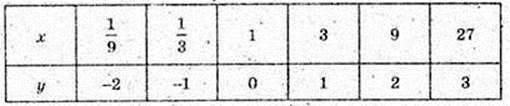
2) f(x) = Iog3x, 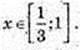
F(х) найб. =Iog31 = 0; 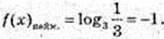
44.
У = Iog3 x
1) y = Iog3x
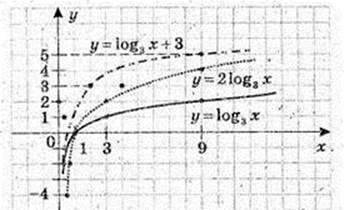
Y = 2log3 x
2) y = Iog3 х + 3
3) у = log3 (х + 3), x > -3
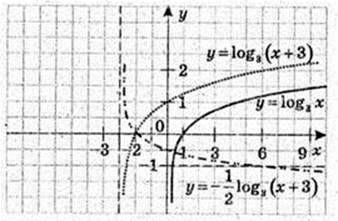
4) 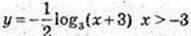
5) у = 1 + Iog3(-x) x < 0
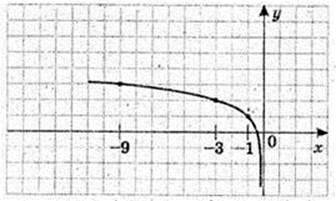
45.
У = lоg2(х +1)
1) х + 1 > 0, x? (-1, +∞) – область визначення: у? (-∞·; +∞) – область значень;
2) x= 0, у = 0, A(0; 0);
3)
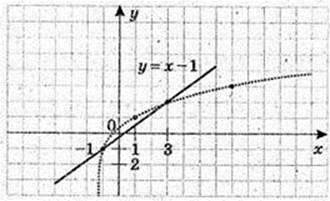

4) A(3; 2), 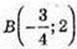 графік функції проходить через т. А(3; 2), не проходить через
графік функції проходить через т. А(3; 2), не проходить через
Т. 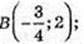
5) Рівняння log2(x + 1) = х – 1 має 2 розв’язки.
46.
1) 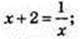 х2 + 2х – 1 = 0;
х2 + 2х – 1 = 0; 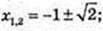
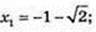
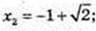
2) x2 + 6 = 7x – 4; x2 – 7x + 10 = 0; x1 = 2; x2 = 5;
3) 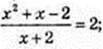
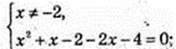
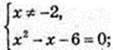
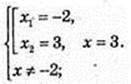
47.
1) х -? 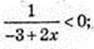 2х – 3 < 0;
2х – 3 < 0; 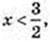
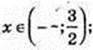
2) x -? 3х2 – 2х – 1 < 0;(3х + 1)(х – 1) < 0;
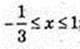
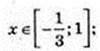
3) х – ? 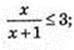
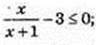
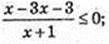
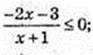
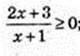
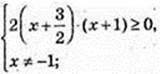
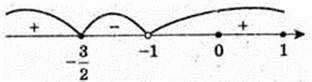
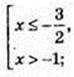
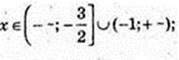
4) |1 + 2x| > 1; 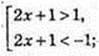
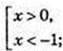 x? (~∞; -1)
x? (~∞; -1) 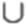 (0; +∞).
(0; +∞).
48.
1) Областю визначення функції 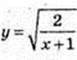 є такі значення х, що
є такі значення х, що 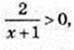
X > -1, x? (-1; +∞);
2) Областю визначення функції 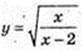 Є такі значення х, що
Є такі значення х, що 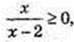
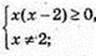
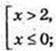 x? (-∞; 0]
x? (-∞; 0] 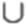 (2; +∞);
(2; +∞);
3) Областю визначення функції 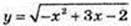 є такі значення х, що
є такі значення х, що
(-x2 + 3х – 2) ≥ 0; -(х2 – 3х + 2) ≥ 0; х2 – 3х + 2 ≤ 0; (х – 1) × (х – 2) ≤ 0; 1 ≤ х <≤ 2.
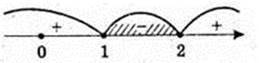
49.
1) x -? 4x-3x-4 =1; x2 – 3х – 4 = 0; (x + 1)(x – 4) = 0; x1 = -1, х2 = 4;
2) x – ? 64x = 4x+2; (43)x= 4x+2; 43x =4x+2; 3x = x2 + 2; x2 – 3x + 2 = 0;x1 = 2,x2 = 1;
3) x – ? 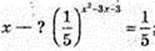 x2 – 3x – 3 = 1; x2 – 3x – 4 = 0; x1 = -1, x2 = 4;
x2 – 3x – 3 = 1; x2 – 3x – 4 = 0; x1 = -1, x2 = 4;
4) 4x-x+1 = 8x. (22)x-x+1 = (23)x; 2х2 – 2х + 2 = 3х; 2х2 – 5x +2 = 0; 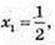 x2 = 2;
x2 = 2;
5) 2x+1 × 5x = 200; 2x+1 × 5x = 25 × 8; 2x+1 × 5 = 52 × 23| : 52 × 23; 2x+1-3 × 5x-2 = 1;
2x-2 × 5x-2= 1; (10)x-2 = 1; x – 2 = 0, x = 2;
6) 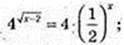
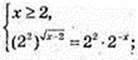
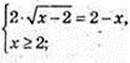
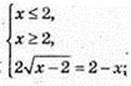 x = 2.
x = 2.
50.
1) x – ? 3x = 2x; 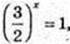 x = 0;
x = 0;
2) x – ? 5 -2x = 4-x; (52)-x = 4-x | : 4-x; 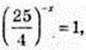 x = 0;
x = 0;
3) x -? 3-x+4 – 25 × 52-x = 0; 3-x+4 – 52+2-x = 0; 34-x -54-x = 0; 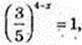 х = 4.
х = 4.
4) x – ? 81× 8x-3 – 9x-1 = 0; 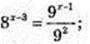
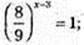 x – 3 = 0, x = 3.
x – 3 = 0, x = 3.
51.
X -?
1) 22x – 2x -12 = 0, 3аміна 2x = t > 0;t2 – t -12 = 0; 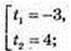 Не підх. t = 4, 2x = 4, x = 2;
Не підх. t = 4, 2x = 4, x = 2;
2) 16x – 4x – 2 = 0, 4x = t, t > 0; t2 – t – 2 = 0; 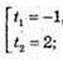 не підх. 4x = 2, 2x = 2, 2х = 1,
не підх. 4x = 2, 2x = 2, 2х = 1, 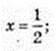
3) 3x + 31-x = 4; 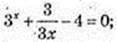 (3x)2 – 4 × 3x + 3 = 0; 3x = t, t > 0, t2 – 4t + 3 = 0
(3x)2 – 4 × 3x + 3 = 0; 3x = t, t > 0, t2 – 4t + 3 = 0
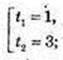
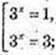 x1 = 0; x2 = 1;
x1 = 0; x2 = 1;
4) 32x+1 +10 × 3x +3 = 0; 3(3x)2 +10 × 3x + 3 = 0, 3x = t, t > 0; 3t2 + 10t + 3 ≠ 0, оскільки t > 0. Розв’язків не iснує.
5) 2 × 9x – 5 × 6 x – 3 × 4 x = 0| : 6 x; 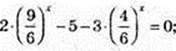
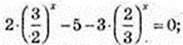
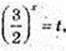
T > 0; 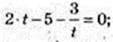 2t 2 – 5t – 3 = 0; t1 = 3,
2t 2 – 5t – 3 = 0; t1 = 3, 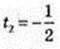 не підх.
не підх. 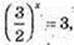
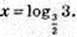
52.
1) х – ?; 5 x+1 -5 x-1 =24; 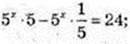
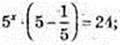
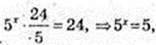
2) x -? 23x × 3 x – 23x-1 × 3x+1 + 288 = 0; 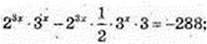
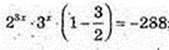
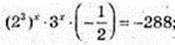 (8 × 3) x = 576; 24 x = 242; х = 2;
(8 × 3) x = 576; 24 x = 242; х = 2;
3) x – ? 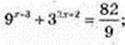
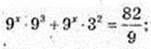
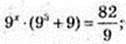
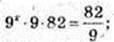
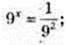 9 x = 9-2; x =-2.
9 x = 9-2; x =-2.
53.
1) x – ? 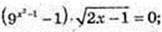
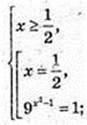
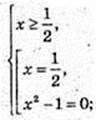
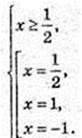
Відповідь: 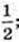 1. Найменший корінь
1. Найменший корінь 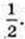
2) x – ? 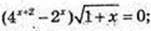
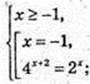
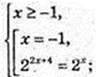
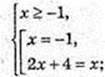
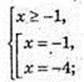
Не підходить. Найменший корінь х = -1.
54.
1) x – ?; 0 = 3 x-1 – 6х × 2-х × 3 x+1; 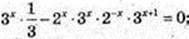
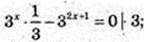 3x – 32x+2 = 0; 3 x = 32x × 32; 3x = 32x+2;
3x – 32x+2 = 0; 3 x = 32x × 32; 3x = 32x+2;
X = 2x + 2, x = -2. A(-2; 0);
2) x -? 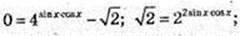
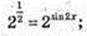
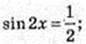
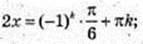
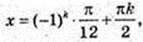
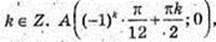 k? Z.
k? Z.
3) x – ? 0 = 2x + 2x-1 + 2x-2 – 3 x + 3x+1 – 3 x – 2;
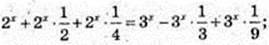
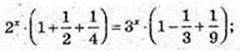
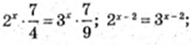 х = 2. А(2 ;0).
х = 2. А(2 ;0).
55.
1) (x, у) – ? 3x-1 ×23x-7 = 129-x; 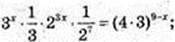
3 x × 23 x = (22 × 3)9 × (22 × 3)- x × 3 × 27;
32x × 25x = 310 × 225; (9 × 25) x = (9 × 25)5 → x = 5,
У = 124. А(5; 20736);
2) (x, у) – ? 9 x+1 + 92x-1 = 54 × 27 x -1;
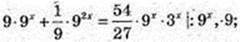 81 + 9 x = 2 × 3 x × 9;
81 + 9 x = 2 × 3 x × 9;
9 x – 18 × 3 x + 81 = 0; 3 x = t, t > 0;
T2 – 18t + 81 = 0; (t – 9)2 = 0; t = 9, 3 x = 32
X = 2, y = 54 × 27 = 1458; А(2; 1458);
3) (x, у) – ? у = 3 × 4x + 2 × 9x i y = 5 × 6x.
X – ? 3 × 4 x + 2 × 9 x = 5 × 6x;
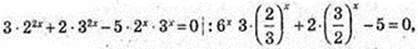
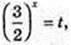 t > 0;
t > 0; 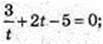
2t2 – 5t? + 3 = 0; t1 = 1, 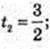
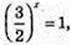
X1 = 0; 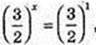 X2 =1. А(0; 5),B(1; 30);
X2 =1. А(0; 5),B(1; 30);
4) (x, у) – ? у = 4x і у = 24 – 2 x + 1
X – ? 4 x = 24 – 2 x +1; 22 x + 2 x × 2 – 24 = 0, 2 x = t, t > 0;
T2 + 2t – 24 = 0; t1 = 4, t2 = -6 не підходить.
2 x = 4, 2 x = 22, x = 2, у = 42 = 16; А(2; 16).
56.
1) x – ? 23-6x > 1; 3 – 6x > 0 | : 3; 1 – 2x > 0;
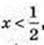
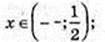
2) 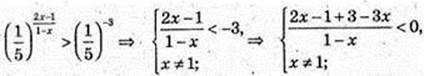
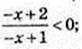
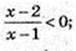
(x – 2) (x – 1) < 0; 1 < x< 2, x? (1; 2)
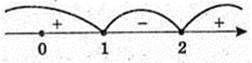
3) x -?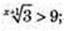
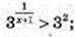
(x + 1) – цілі значення і (х + 1) > 0.
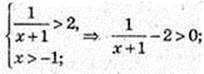
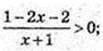
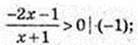
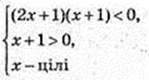
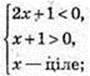
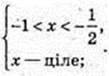 немає розв’язків;
немає розв’язків;
4) 3x > 2, x > log3 2, x? (Iog3 2;+ ∞);
5) x – ? 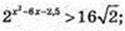
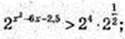
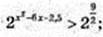 x2 – 6x – 2,5 > 4,5;
x2 – 6x – 2,5 > 4,5;
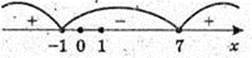
X2 – 6x – 7 > 0; (x + 1)(х – 7) > 0; x? (-∞; -1)  (7; + ∞),
(7; + ∞),
57.
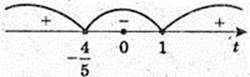
1) x – ? 52 x +1 > 5 x + 4; 52x × 5 – 5 x – 4 > 0; 5 x = t, t > 0;
5t2 – t – 4 > 0; (t -1)(5t + 4) > 0; t > 0, t > 1, 5x > 1, x > 0. x? (0; ∞);
2) 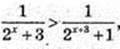 x – ?
x – ?
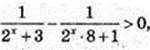 2х = t, t> 0;
2х = t, t> 0; 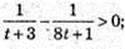
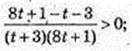
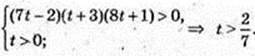
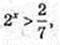
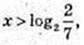
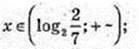
3) x – ? 22х+2 + 6x – 2 × 32x+ 2 > 0;
22x × 4 + 2x × 3x – 2 × 32x × 9 > 0 : (2x × 3x);
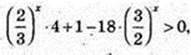
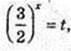 t > 0
t > 0 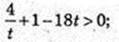
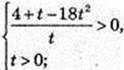
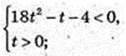
T – ? 18t2 – t – 4=0. 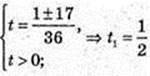
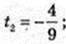
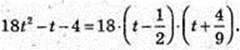
T – ? 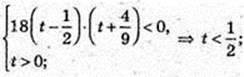
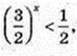
X < Iog15 0,5; 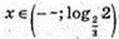 або x? ( -∞; Iogl,5 0,5).
або x? ( -∞; Iogl,5 0,5).
4) x – ? 3x+ 1 – 5 × 2x ≤ 2x+2 – 3x; 3x × 3 + 3× ≤ 2x × 22 + 5 × 2х; 3x x 4 ≤ 2x × 9 |: 9, : 4
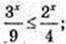
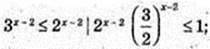
X – 2 ≤ 0, x ≤ 2, x? (-∞; 2].
58.
1) (x, у) – ? 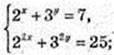
3аміна 2х = t, 3y = z, t > 0, z > 0.
22x = t2, 32у = z2. 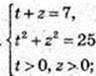 в квадрат
в квадрат 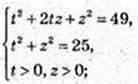
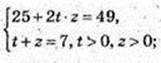
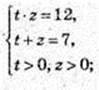
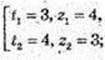
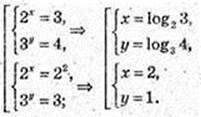
Відповідь: (log23; Iog3 4), (2; 1).
2) (х, у) – ?
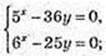
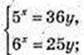
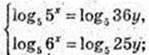
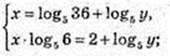
(Iog5 36 + Iog5 у) × Iog5 6 = 2+ Iog5 у;
(Iog5 62) × log5 6 + (log5 6) × Iog5 у – 2 – Iog5 у = 0;
(2 Iog5 6 – 2) + Iog5 у × (Iog5 6 – 1) = 0;
2 × (Iog5 6 – 1) – (Iog5 6 + 1) + Iog5 у × (Iog5 6 – 1) = 0;
Поділимо рівняння на число (log5 6 – 1) ≠ 0.
Маємо 2 × (Iog5 6 + 1) + log5 у = 0;
Iog5 у = -2 × (Iog5 6 + Iog5 5);
Log5 у = -2 × Iog5 30 = Iog5 30-2 = log5 900-1;
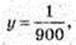 x – ?
x – ? 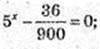
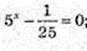 5x = 5-2, xχ = -2.
5x = 5-2, xχ = -2. 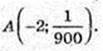
3) (х, у) -? 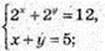
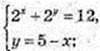
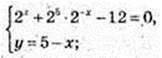
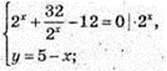 (2x)2 – 12 × 2x + 32x = 0;
(2x)2 – 12 × 2x + 32x = 0;
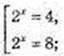
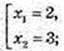 y1 = 3, y2 = 2(2; 3), (3; 2).
y1 = 3, y2 = 2(2; 3), (3; 2).
4) (х, у) – ? 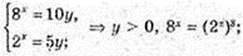 (5y)3 = 10y;
(5y)3 = 10y;
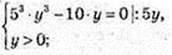
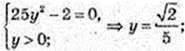
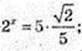
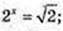
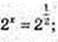
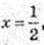
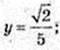
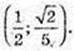
59.
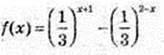
1) x =0; y = ? 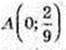
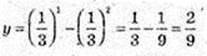
Y = 0, x – ? 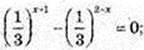
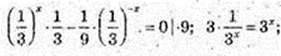 3 = (3x)2,
3 = (3x)2,
3 = 32x, 1 = 2х, 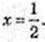 В(0,5; 0),
В(0,5; 0), 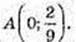
2) х – ? 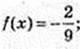
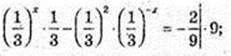
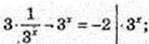 3 – (3x)2= -2 × 3x;
3 – (3x)2= -2 × 3x;
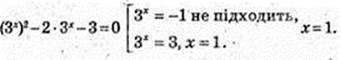
3) х -? 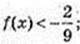
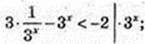
3 – (3x)2 < -2 × 3x; (3x)2 – 2 × 3x – 3 > 0;
(3x + 1) × (3x – 3) > 0; 3x – 3 > 0, 3x > 3x, x >1, х? (1;+ ∞).
4) 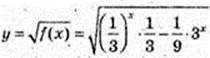 х – ?
х – ? 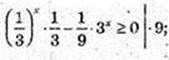
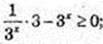
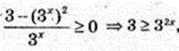 1 ≥ 2х,
1 ≥ 2х, 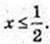 x? (-∞; 0,5).
x? (-∞; 0,5).
60.
500 = 100 × ek-12, 5 = е12k, е12k т= 5.
100 × е48k = 100 × (e12k)4 = 100 × 54 = 100 × 625 = 62500.
62.
1) х – ?
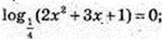 2х2 + 3х + 1 = 1;
2х2 + 3х + 1 = 1; 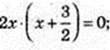 x1 = 0,
x1 = 0, 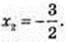
2) x – ? Iog2 (х – 7) = Iog2 (4 – х); 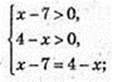
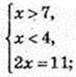
Немає розв’язків.
3) x -? 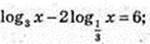
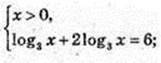
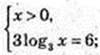
X = 32, x = 9.
4) x -? log2(x – 2) = log2(x2 – x – 17);
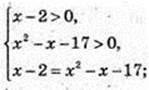
X 2 – 2x -15 = 0, x1 = -3, не підходить. x2 = 5; x = 5.
5) x -? Iog5-x (x2 – 2x + 65) = 2;
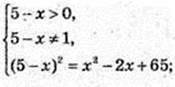 25 -10х + х2 = х2 – 2х + 65;
25 -10х + х2 = х2 – 2х + 65;
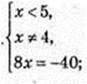 x = -5.
x = -5.
63.
1) x -? Iog3 (х + 1) + Iog3 (x+ 3) = 1.
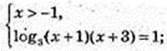
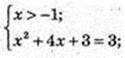
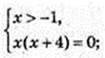 x = 0.
x = 0.
2) x -? Ig2 x = 4 – 3 Ig х. 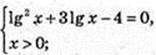
Ig x = t, t2 + 3t – 4 = 0; 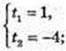
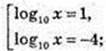 x1=10, x2 = 10-4.
x1=10, x2 = 10-4.
3) x -? 6logx 2 – 6log4x + 7 = 0;
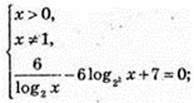
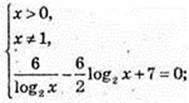
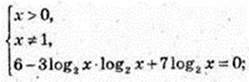
Iog2 x = t, 3t2 – 7t – 6 = 0.
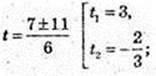
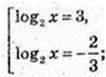
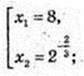 x1 = 8;
x1 = 8; 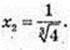
4) x -? 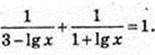
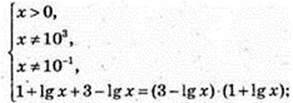
4 = 3 + 2 Ig x – Ig2 x; Ig2 x – 2 Ig x + 1= 0; (lg x -1)2 = 0; Ig x = 1, x = 10.
64.
1) x -? 100lg(x+20> = 1000. 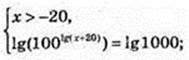
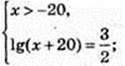
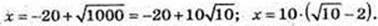
2) x -? 54lgx = 62,5x; 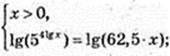
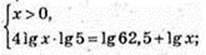
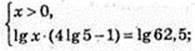 Ig x × (lg 54 – Ig 10) = Ig 62,5;
Ig x × (lg 54 – Ig 10) = Ig 62,5;
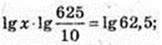 Ig x = 1, x = 10.
Ig x = 1, x = 10.
3) x-? хlgx+2=1000.
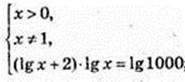
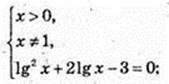
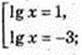
X1= 10, x2= 103.
4) x -? 
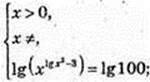
(Igx2 – 3) × Igx = 2; (2lgx – 3)lgx – 2 = 0;
2 Ig2 x – 3 lgx – 2 = 0; Igx = t, 2t2 – 3t – 2 = 0;
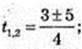 t1 = 2,
t1 = 2, 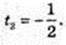
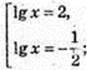
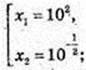 x1 = 100,
x1 = 100, 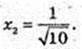
65.
1) 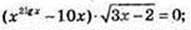
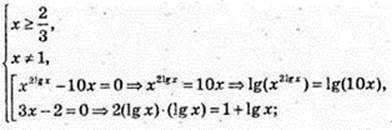 2lg2x – lgx -1= 0;
2lg2x – lgx -1= 0;
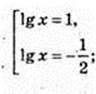
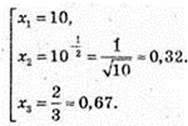 Найменший корінь
Найменший корінь 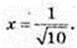
2) x – ? 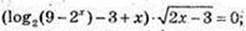
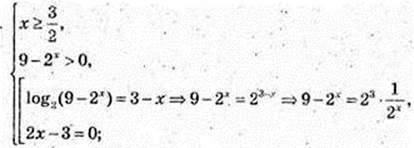
9 × 2х – (2x)2 = 8; (2x)2 – 9 × 2x + 8 = 0;
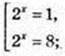
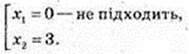
Маємо 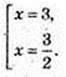 Найменший корінь
Найменший корінь
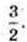
66.
1) y = x(1 – Ig 5), у = lg(4x – 12);
X – ? y1 = y2
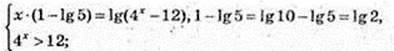
X × Ig 2 = lg(4x – 12); lg(2x) = lg(4x – 12); 2х = 4 x = 12; 4х – 2х – 12 = 0; 2 x = t, t > 0;
T2 – t – 12 = 0; it1 = 4, t2 = -3 – не підходить; 2 x = 4; 2 x = 22; x = 2.
X = 2; y = 2 Ig 2 = Ig 22 = Ig 4. А(2; Ig 4).
2) 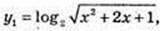 y2 = 6 – Iog2(x + 1)2;
y2 = 6 – Iog2(x + 1)2;
X – ? y1 = y2; y1 = Iog2 |x + 1|; y2 = 6 – 2 Iog2 |х + 1|; x ≠ -1;
Iog2 |x + 1| = 6 – 2 log2 |х + 1|; 3 log2 |x + 1| = 6; log2 |x + 1| = 2; |x + 1| = 4;
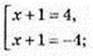
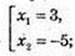
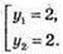 А(3; 2), В(-5; 2).
А(3; 2), В(-5; 2).
3) x – ? y1 = y2; y1 = lg(35 – x3), y2 = 3 lg(5 – x);
Lg(35 – x3) = 3 lg(5 – x); 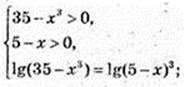
35 – x3 = 53 – 3 × 52 × x + 3 × 5 × x2 – x3; 15×2 – 75x + 125 – 35 = 0 | :5;
3×2 – 15x + 18 = 0; 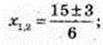
X1 = 3,… y1 = 3 Ig 2; x2 = 2, y2 = 3 Ig 3. А(3;· 3 Ig 2), 5(2; 3 Ig 3).
4) x – ? y= 4 – Ig x і 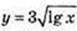 перетинаються?
перетинаються?
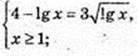
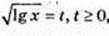 t2 + 3t – 4 = 0;
t2 + 3t – 4 = 0; 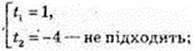
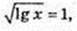 Igx = 1, x =10, y = 3. А(10; 3).
Igx = 1, x =10, y = 3. А(10; 3).
67.
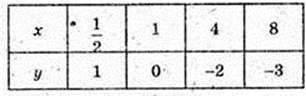
1) log2x = – x + 1.
Y1 = log2 x
X | 1 | 2 | 4 | 16 |
Y | 0 | 1 | 2 | 4 |
Y2 = – x + 1
X | 1 | 4 |
Y | 0 | -3 |
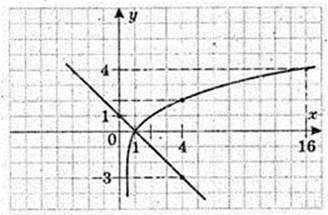 А(1; 0)
А(1; 0)
2) x – ? 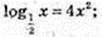
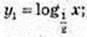
Y 2 = 4 x 2;
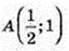
68.
1) х – ? log5(3x – 1)< 1; 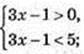
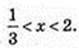 1 < 3х < 6;
1 < 3х < 6; 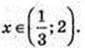
2) x – ? Iog(x2 – 2х) – 3 > 0;
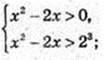
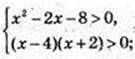
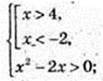
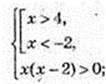
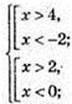
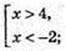
X є (-∞; -2) 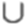 (4; +∞).
(4; +∞).
3) x – ? (Iog2 x)2 ≤ 4; x > 0; 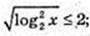 |log2 х| ≤ 2;
|log2 х| ≤ 2;
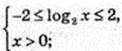
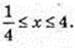
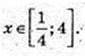
4) x – ? 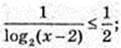
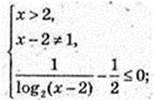
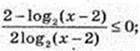
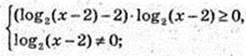
Iog2(x – 2) = t; 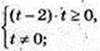
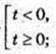
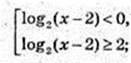
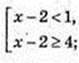
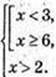 x? (2; 3)
x? (2; 3)  [6; +∞).
[6; +∞).
69.
1) x – ? lg(x2 – 3) > lg(a + 3);
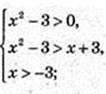
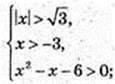
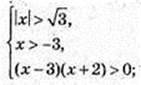
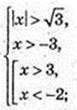
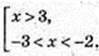 x? (-3; -2) u (3; +∞),
x? (-3; -2) u (3; +∞),
2) x – ? lg2x – 2lgx – 8 ≤ 0, x > 0; lgx = t; t2 – 2t – 8 ≤ 0; t1 = 4, t2 = -2; (t – 4)(t + 2) ≤ 0;
-2 ≤ t ≤ 4; -2 ≤ Ig x ≤ 4; 10-2 ≤ x ≤ 104; 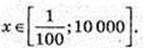
3) x – ? 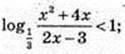
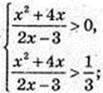
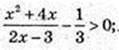
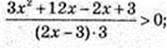
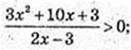
X – ? 3×2 + 10x + 3 = 0; a = -3, 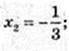
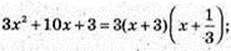
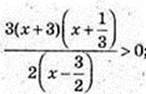
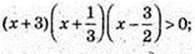
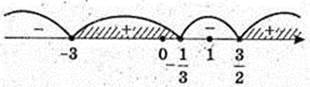
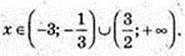
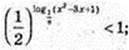
4) x – ? 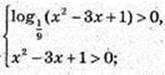 -log9(x2 – 3a + 1) > 0;
-log9(x2 – 3a + 1) > 0;
Log9(x2 – 2 + 1) < 0; 0 < x2 – 3x + 1 < 1; 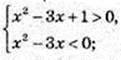
X2 – 3x + 1 = 0; 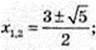
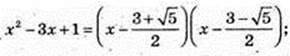
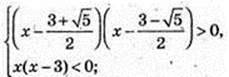
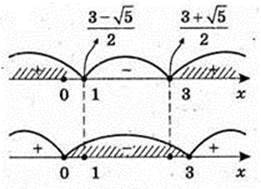
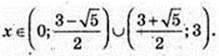
70.
1) (x × y) – ?
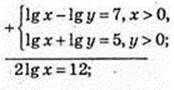
Ig x = 6, x = 106; lgy = -1; у = 10-1. A(106; 10-1).
2) (x, y) – ?
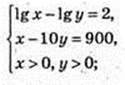
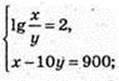
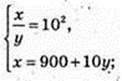
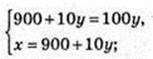
90у = 900; у = 10; х = 1000; А(1000; 10).
3) (x, y) – ?
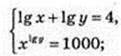
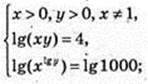
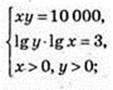
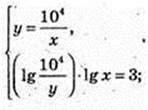
(4 – Ig х) × Ig x = 3; Ig2 x – 4 Ig х + 3 = 0; 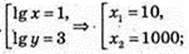
Y1 = 103 – 1000; у2 = 10. А(10; 1000), В(1000; 10).
4) 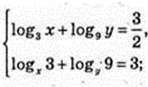
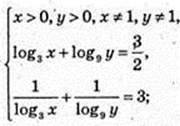 Iog3 x = t, Iog3y = 2;
Iog3 x = t, Iog3y = 2;
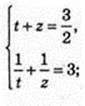
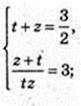
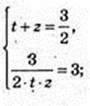
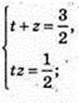
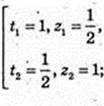
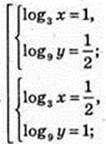
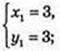
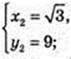 (3; 3),
(3; 3), 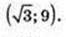
71.
F(x) = log3x + 3log3x, x > 0
1) x – ? 0 = Iogзx +3Iog3x1, x > 0; Iog3х × (Iog3х + 3) = 0;
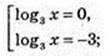
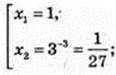 A(1; 0),
A(1; 0), 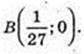
Графік функції не перетинається з віссю Oy.
2) x – ? f(x) = -2; 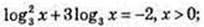
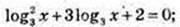
Log3 x = t; t3 + 3t + 2 = 0; t1 = -1; t2 = -2;
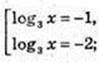
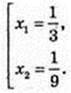
3) x – ? f(x) < 2; 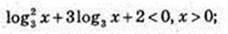
T2 + 3t + 2 < 0; (t + 1)(t + 2) < 0; -2 < t <-1; -2 < log3х < -1;
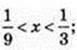
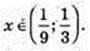
4) x – ? 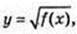 f(x) > 0;
f(x) > 0;
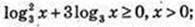 Iog3 x × (Iog3 x + 3) ≥ 0; t × (t + 3) ≥ 0;
Iog3 x × (Iog3 x + 3) ≥ 0; t × (t + 3) ≥ 0;
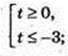
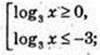
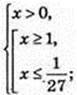
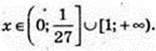
72.
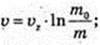 m – ?
m – ? 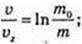
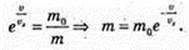
73.
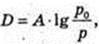 p – ?
p – ?