Правила знаходження первісних – ПРОПОРЦІЇ. ВІДСОТКИ

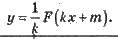
Related posts:

1. Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила диференціювання Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних: Правило 2. Якщо функція у = f(x) має похідну в точці х, то і […]...
2. Правила знаходження первісних – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Правила знаходження первісних 1. Якщо є первісною для , а – первісною для , то є первісною для. 2. Якщо є первісною для , а k – стале число, то є первісною для . 3. Якщо є первісною для , а k і b – сталі, причому , […]...
3. Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх . Операція знаходження первісної F для даної функції називається Інтегруванням. Теорема 1. Будь-яка неперервна на відрізку функція має первісну функцію. Лема. Якщо на деякому проміжку, то на цьому проміжку, де C […]...
4. Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
5. Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...
6. Формули скороченого множення – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Формули скороченого множення (а + b)2 = а2 + 2аb + b2 (квадрат суми); (a – b)2 = а2 – 2ab + b2 (квадрат різниці); A2 – b2 = (a + b)(a – b) (різниця квадратів); (a + b)3 = а3 + 3а2b + 3ab2 + b3 (куб суми); […]...
7. Похідні елементарних функцій – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Похідні елементарних функцій Y = f(x) Y = f'(x) Y = f(x) Y = f'(x) Y = c (c = const) Y’ = 0 У = ax + b Y’ = a Y = xn Y’ = nxx-1 Y = x Y’ = 1 Y = 1/x Y’ = […]...
8. Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
9. Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
10. ЯК ЗА ПЕРВІСНИХ ЧАСІВ ВИНИКАЛИ МИСТЕЦТВО І РЕЛІГІЙНІ ВІРУВАННЯ Розділ І ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ § 7. ЯК ЗА ПЕРВІСНИХ ЧАСІВ ВИНИКАЛИ МИСТЕЦТВО І РЕЛІГІЙНІ ВІРУВАННЯ 1. МИСТЕЦТВО ЗА ПЕРВІСНОЇ ДОБИ Що і чому зображували первісні митці? Тривалий час учені нічого не знали про первісне мистецтво. Однак близько 130 років тому перші наскельні малюнки знайшов археолог Марселіно Саутуола, який проводив розкопки в підземній […]...
11. Відсотки. Знаходження відсотків від числа Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 5. ДЕСЯТКОВІ ДРОБИ 37. Відсотки. Знаходження відсотків від числа На практиці люди часто користуються сотими частинами величин. Наприклад, сота частина гектара – 1 ар (1 сотка), сота частина століття – 1 рік, сота частина гривні – 1 копійка, сота частина метра – 1 сантиметр. Для сотої […]...
12. Відсотки. Знаходження відсотків від числа Урок 117 Тема. Відсотки. Знаходження відсотків від числа Мета: сформувати вміння, відпрацювати навички знаходження відсотків від числа; провести діагностику засвоєння знань і вмінь. Тип уроку: застосування знань, навичок і вмінь. Хід уроку I. Розминка Усні вправи 1. Розчин містить сіль і воду. Сіль становить 9% розчину. Скільки відсотків становить вода? 2. Сплав складається з міді, […]...
13. Відсотки. Знаходження відсотків від даного числа Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ § 42. Відсотки. Знаходження відсотків від даного числа Під час різних обчислень людям часто доводиться знаходити частини числа: (половину), (четвертину), і т. д. Найзручніше в таких обчисленнях знаходити соті частини числа, або відсотки (проценти)1, оскільки при цьому доводиться множити чи ділити на число 100. Відсотком (процентом) називається […]...
14. Пропорція, члени пропорції. Основні властивості пропорції Урок № 4 0 Тема. Пропорція, члени пропорції. Основні властивості пропорції Мета: сформувати уявлення учнів про зміст понять пропорція, члени пропорції, основна властивість пропорції та виробити вміння застосовувати ці поняття під час розв’язування типових завдань, що передбачають їх застосування. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього завдання. Актуалізація опорних знань @ […]...
15. Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
16. Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
17. Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
18. ЯК БУЛО ОРГАНІЗОВАНО ЖИТТЯ СУСПІЛЬСТВА ЗА ПЕРВІСНИХ ЧАСІВ Розділ І ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ § 5. ЯК БУЛО ОРГАНІЗОВАНО ЖИТТЯ СУСПІЛЬСТВА ЗА ПЕРВІСНИХ ЧАСІВ 1. РІД (РОДОВА ОБЩИНА) В ПЕРВІСНОМУ СУСПІЛЬСТВІ Які були основні ознаки родової общини? У первісні часи люди не могли існувати окремо. Колективне полювання, будівництво нового житла вимагали зусиль великої кількості людей. Спільні праця, житло і розвиток мови згуртовували […]...
19. Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
20. Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
21. Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
22. У ЧОМУ ОСОБЛИВОСТІ ОРГАНІЗАЦІЇ ВЛАДИ ЗА ПЕРВІСНИХ ЧАСІВ Розділ І ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ § 6. У ЧОМУ ОСОБЛИВОСТІ ОРГАНІЗАЦІЇ ВЛАДИ ЗА ПЕРВІСНИХ ЧАСІВ 1. ОРГАНІЗАЦІЯ ВЛАДИ ЗА ПЕРВІСНИХ ЧАСІВ Як здійснювалося керівництво родовою общиною? Члени родової общини були рівними між собою й мали рівні права. Утім, кожний колектив потребує управління. Керувати родовою общиною, її господарством було не простою справою. Тому на […]...
23. ОСНОВНІ СТОЯНКИ ТА ПАМ’ЯТКИ ПЕРВІСНИХ ЛЮДЕЙ НА ТЕРИТОРІЇ УКРАЇНИ ПРАКТИЧНЕ ЗАНЯТТЯ 2 Розділ 1 ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ §8.ОСНОВНІ СТОЯНКИ ТА ПАМ’ЯТКИ ПЕРВІСНИХ ЛЮДЕЙ НА ТЕРИТОРІЇ УКРАЇНИ ПРАКТИЧНЕ ЗАНЯТТЯ 2 1. Про що свідчать археологічні знахідки зі стоянки в Мізині на Чернігівщині? На території України досліджено кількасот стоянок, віднесених до часів пізнього палеоліту. Найвідоміші з них розташовані в селах Мізині на Чернігівщині, Межиріччі на Черкащині, Добраничівці […]...
24. Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
25. ПРАВИЛА ЗНАХОДЖЕННЯ НЕВІДОМИХ ВІД’ЄМНИКА І ЗМЕНШУВАНОГО. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 58. ПРАВИЛА ЗНАХОДЖЕННЯ НЕВІДОМИХ ВІД’ЄМНИКА І ЗМЕНШУВАНОГО. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: ознайомити учнів з правилом знаходження невідомих від’ємника і зменшуваного; управляти у розв’язуванні задач; вдосконалювати обчислювальні навички; розвивати математичне мовлення; виховувати культуру письма, інтерес до навчання. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ ВИВЧЕНОГО […]...
26. Відсотки. Записування відсотків десятковим дробом або натуральним числом Урок № 54. Тема. Відсотки. Записування відсотків десятковим дробом або натуральним числом Мета уроку. Ознайомити з означенням відсотка, уміти записувати відсотки числом. Обладнання. Таблиця “Відсотки”. Хід уроку I. Перевірка домашнього завдання Учитель з’ясовує стан виконання домашньої роботи. Якщо у когось виникли запитання, то за допомогою учнів і самого учителя дають на них відповіді. II. Тестові […]...
27. ЗАНЯТТЯ ТА СПОСІБ ЖИТТЯ ПЕРВІСНИХ ЛЮДЕЙ Розділ 1 ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ § 5. ЗАНЯТТЯ ТА СПОСІБ ЖИТТЯ ПЕРВІСНИХ ЛЮДЕЙ – Роздивіться ілюстрації. Про які заняття людей свідчать художні реконструкції? Які знаряддя праці використовують зображені на картинах люди? – Чи відрізняються заняття й спосіб життя людей на картинах? Чим саме? – Спробуйте витлумачити поняття привласнювальні та відтворювальні форми господарювання людей. […]...
28. Складені задачі, що включають знаходження дробу від числа. Повторення правила множення числа на добуток Подання дробу як частки двох чисел (№№ 797-805) Тема. Складені задачі, що включають знаходження дробу від числа. Повторення правила множення числа на добуток Подання дробу як частки двох чисел (№№ 797-805). Мета. Закріплювати вміння учнів розв’язувати задачі, що включають знаходження дробу від числа; ознайомити учнів із дробами як частками двох чисел, вчити розв’язувати відповідні задачі; повторити правило множення числа на добуток та вправляти […]...
29. Правила переносу слів – Фонетика Українська мова Фонетика Правила переносу слів 1. Слова з одного рядка в другий слід переносити складами (кни-га, паль-ці, по-ло-ва, са-дів-ник, Хар-ків). 2. Сполучення літер ЙО, ЬО при перенесенні нерозриваються (йо-го, ма-йор, ко-льо-ро-вий, сьо-го-дні, цьо-му). 3. З двох однакових приголосних між голосними один залишається в попередньому рядку, а другий переноситься в наступний (баштан-ник, ран-ні); якщо друга […]...
30. Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
31. Правила оформлення цитат і прямої мови ДІЛОВА УКРАЇНСЬКА МОВА Розділ 5. Синтаксичні структури діловодства Правила оформлення цитат і прямої мови Розділові знаки при цитатах і діалозі Цитати виділяються лапками. Якщо цитата супроводжується словами автора, то вона оформляється як пряма мова. Якщо цитата наводиться не повністю, то пропуск позначається крапками: ”Влада має велику кількість інструментів, якими регулюються різні сфери суспільної життєдіяльності…”, – […]...
32. Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...
33. Відношення та пропорції Математика – Алгебра Множення і ділення звичайних дробів Відношення та пропорції Відношенням двох чисел називається частка цих чисел. Відношення показує, у скільки разів одне число більше від другого або яку частину становить одне число від ­другого. Щоб знайти відношення двох величин, вони мають бути виміряні однією й тією ж одиницею вимірювання. Напри­клад, відношення 3 км […]...
34. Відсотки. Вираження числа відсотками Урок № 55. Тема. Відсотки. Вираження числа відсотками Мета уроку. Уміти виражати зміну величини різними способами. Обладнання. Картки для індивідуальної роботи з учнями, таблиця “Відсотки”. Хід уроку I. Актуалізація опорних знань 1. Що означає знак %? Дати означення відсотка. 2. Знайти 1 % чисел: 6000; 200; 450; 70; 20. 3. В класі присутні 92 % […]...
35. СУСПІЛЬНА ОРГАНІЗАЦІЯ ТА ОРГАНІЗАЦІЯ ВЛАДИ ЗА ПЕРВІСНИХ ЧАСІВ Розділ 1 ЖИТТЯ ЛЮДЕЙ ЗА ПЕРВІСНИХ ЧАСІВ § 6. СУСПІЛЬНА ОРГАНІЗАЦІЯ ТА ОРГАНІЗАЦІЯ ВЛАДИ ЗА ПЕРВІСНИХ ЧАСІВ – Роздивіться реконструкцію Чатал-Гуюка – одного з найбільших серед перших міст (було розташоване на території сучасної Туреччини). На які особливості забудови міста ви звернули увагу? – Поділіться припущеннями, які буденні справи визначали життя його мешканців. – Поміркуйте, що […]...
36. Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
37. Інтеграл та його застосування 175. 1) F(x) = 9×2 – 2х +1? F(x) – первісна для функції у = f(x) на заданому проміжку, якщо для всіх x з цього проміжку виконується співвідношення F'(x) = f(x). Дійсно, F'(x) = 18х – 2 = 2(9х – 1) = f(x), -∞ < х < +∞, що й треба було довести. 2) Аналогічно. […]...
38. Правила макроеволюції МЕДИЧНА БІОЛОГІЯ Розділ 2 ПОПУЛЯЦІЙНО-ВИДОВИЙ РІВЕНЬ ОРГАНІЗАЦІЇ ЖИТТЯ ТА МІСЦЕ ЛЮДИНИ В НЬОМУ 2.3. Закономірності і проблеми макроеволюції та антропогенезу 2.3.4. Правила макроеволюції Зіставлення характеру розвитку груп дозволило сформувати основні правила макроеволюції. Правило незворотності еволюції (Л. Долло, 1893): еволюція, як і будь-який розвиток, – процес незворотний; повернення таксону у філогенезі до стану, пройденого раніше, неможливий. […]...
39. Пропорція. Основна властивість пропорції Розділ 3 Відношення і пропорції §21. Пропорція. Основна властивість пропорції Відношення 12 : 3 і 20 : 5 рівні, оскільки їх значення дорівнюють 4. Тому можна записати рівність Рівність двох відношень називають пропорцією. Слово “пропорція” походить від латинського proportio, що означає “співрозмірність”, тобто певне відношення частин між собою. За допомогою букв пропорцію записують так: Ці […]...
40. Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...