Приклади функцій і їх графіків
Математика – Алгебра
Функції
Приклади функцій і їх графіків
Лінійна функція
Лінійною називається функція, яку можна задати формулою 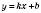 , де х – аргумент, а k і b – дані числа.
, де х – аргумент, а k і b – дані числа.
Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до осі абсцис,- графік деякої лінійної функції.
Через дві точки можна провести одну й тільки одну пряму, тому для побудови графіка лінійної функції
Приклад
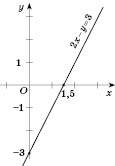
Побудуйте графік функції
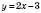 .
.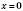 ,
, 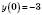 ;
; 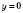 ,
, 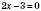 ,
, 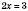 ,
, 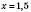 .
.| X | 0 | 1,5 |
| Y | -3 | 0 |
Побудуємо графік (див. рисунок).
Якщо в лінійній функції
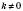 , то графік функції
, то графік функції 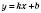 перетинає вісь абсцис;
перетинає вісь абсцис;якщо
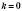 ,
, 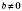 , то графік функції – пряма, паралельна осі абсцис;
, то графік функції – пряма, паралельна осі абсцис;якщо
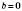 ,
, 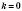 , графік функції збігається з віссю абсцис.
, графік функції збігається з віссю абсцис.Графіки двох лінійних функцій перетинаються, якщо їх кутові коефіцієнти різні, і паралельні, якщо їх кутові коефіцієнти однакові.
Можна знайти координати точки перетину прямих, не виконуючи побудови графіків функцій. Так, якщо прямі задані рівняннями
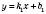 і
і 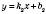 , то досить розв’язати систему рівнянь:
, то досить розв’язати систему рівнянь: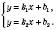
Лінійну функцію, що задається формулою
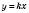 , де
, де 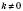 , називають Прямою пропорційністю.
, називають Прямою пропорційністю.Графік прямої пропорційності – пряма, що проходить через початок координат. Якщо
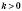 , графік лежить у I і III координатних чвертях, а якщо
, графік лежить у I і III координатних чвертях, а якщо 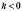 – то у II і IV координатних чвертях.
– то у II і IV координатних чвертях.Приклади
1)
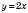 ,
, 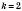 ,
, 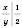 .
.2)
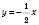 ,
, 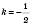 ,
, 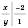 .
.Побудуємо в одній системі координат графіки функцій
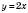 і
і 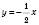 (див. рисунок).
(див. рисунок).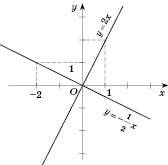
Обернена пропорційність
Функцію, задану формулою 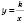 , де х – незалежна змінна,
, де х – незалежна змінна, 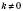 – дане число, називають оберненою пропорційністю.
– дане число, називають оберненою пропорційністю.
Область визначення функції 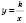 – множина всіх чисел, крім 0.
– множина всіх чисел, крім 0.
Графік функції 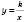
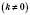 – гіпербола, симетрична відносно початку координат. Коли
– гіпербола, симетрична відносно початку координат. Коли 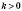 , вітки такої гіперболи розміщені в I і III координатних кутах, коли
, вітки такої гіперболи розміщені в I і III координатних кутах, коли 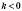 – у II і IV.
– у II і IV.
Як приклад побудуємо графік функції 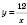 . Заповнимо таблицю (значення x задаємо, y – обчислюємо за формулою
. Заповнимо таблицю (значення x задаємо, y – обчислюємо за формулою 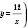 :
:
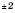
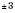
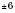
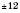
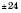
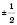
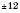
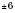
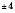
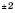
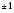
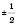
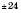
Нанесемо отримані точки на координатну площину. Сполучивши ці точки плавною лінією, отримаємо графік (див. рисунок):
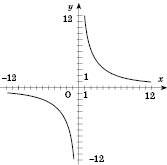
Зверніть увагу на поводження графіка поблизу осей координат. Графік до них нескінченно наближається, але не перетинає. Дійсно, 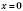 не входить до області визначення, отже точки перетину з віссю Oy немає.
не входить до області визначення, отже точки перетину з віссю Oy немає. 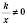 ні при якому значенні х, значить, якщо
ні при якому значенні х, значить, якщо 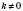 , точки перетину з віссю Ox немає.
, точки перетину з віссю Ox немає.
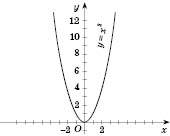
Функція
Заповнимо таблицю (значення x задаємо, y – обчислюємо за формулою y = x2).
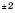
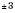
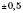
Нанесемо знайдені точки на координатну площину. Сполучивши ці точки, отримаємо графік функції 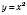 (див. рисунок нижче).
(див. рисунок нижче).
Область визначення цієї функції – множина всіх дійсних чисел.
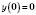 . Графік проходить через початок координат
. Графік проходить через початок координат 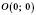 .
.
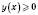 при всіх значеннях х. Усі точки графіка розташовані не нижче осі Оx.
при всіх значеннях х. Усі точки графіка розташовані не нижче осі Оx.
Протилежним значенням аргументу відповідають рівні значення функції, тобто графік симетричний відносно осі ординат.
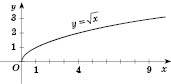
Функція
Область визначення – множина всіх невід’ємних дійсних чисел.
Графік – одна вітка параболи, яка розташована в I координатному куті (див. рисунок).