Пряма пропорційність. Пропорційні величини
Урок № 4 2
Тема. Пряма пропорційність. Пропорційні величини
Мета: сформувати уявлення учнів про пряму пропорційну залежність величин, ознайомити із прикладами таких величин, що їх учні зустрічають у повсякденному житті та під час вивчення шкільних предметів; сформувати вміння розв’язувати задачі цього типу складанням пропорції.
Тип уроку: засвоєння знань, умінь, навичок.
Хід уроку
І. Перевірка домашнього завдання
1. Тестові завдання
Варіант 1 | Варіант 2 |
1. | |
1) 3 : 0,5 = 2 : 12; 2) 2 : 5 = 1 3) 7 : 2 = 14 : 4; 4) 5 : 10 = 4 : 2 | 1) 3) |
2. Яке з поданих чисел треба поставити замість зірочки, щоб рівність стала правильною? | |
3 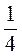 1) 1 |
1) 2 |
3. Яке з поданих чисел є кореням рівняння | |
4,2 : 0,21 = 350 : х? 1) 1,75; 2) 175; 3) 1750; 4) 17,5 | 22,22 : 2,2 = 4,444 : х? 1) 4,4; 2) 0,44; 3) 44; 4) 440 |
2. Під час виконання тестових завдань вибірково (у “слабких” учнів) перевіряємо якість виконання домашнього завдання.
ІІ. Актуалізація опорних знань (під час виконання тестових завдань)
III. Засвоєння знань учнів
@ Викладення нового матеріалу цього уроку проводимо традиційно: спочатку наводимо приклади прямо пропорційних величин, що знайомі учням або з повсякденного життя (вартість покупки і кількість), або ж з вивченого раніше матеріалу (час і відстань при сталій швидкості і т. ін.), а потім від конкретних прикладів переходимо до загального означення.
Дві величини називаються прямо пропорційними, якщо за умови збільшення (зменшення) однієї величини в кілька разів інша величина також збільшується (зменшується) у стільки ж разів.
Після формування уявлень про прямо пропорційні величини треба переходити до розв’язування вправ. Важливо, щоб діти зрозуміли: прямо пропорційні величини – такі, для яких можна скласти істинну пропорцію.
Тому спочатку вчитель, а потім вже діти самостійно (на наступному етапі уроку) розв’язують задачі за схемою, аналогічною до тієї, що ми складаємо під час розв’язування прикладу 1.
Приклад 1. За 3,2 кг товару заплатили 11, 52 грн. Скільки треба заплатити за 1,5 кг такого товару?
Розв’язання. Запишемо умову задачі у вигляді таблиці, позначивши шукану величину за х
І покупка 11 покупка |
| 3,2 кг 1,5 кг | 11,52 грн Х грн |
|
@ Дуже важливо, щоб учні усвідомили, що перед складанням пропорції необхідно пересвідчитися в тому, що величини є дійсно прямо пропорційними, і робили це не формально. Тільки після цього стрілками показуємо, що зміна першої і другої величини одного напрямку (перша зменшилась і друга зменшується у стільки ж разів, тому стрілки умовно спрямовані в один бік) і складаємо рівняння у вигляді пропорції та розв’язуємо його:
3,2 : 1,5 = 11,52 : х; 3,2 – х = 1,5 – 11,52; 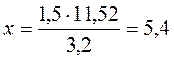 .
.
Отже, вартість другої покупки 5,4 грн.
IV. Формування вмінь
Усні вправи
1. Які з величин прямо пропорційні:
А) маса товару і його вартість;
Б) довжина дроту і його вартість;
В) маса тіла і його об’єм;
Г) периметр квадрата і довжина його сторони;
Д) площа квадрата і довжина його сторони;
Є) довжина ребра куба і його об’єм?
2. Які з наступних величин є прямо пропорційними, а які обернено пропорційними:
А) кількість хлібин та їхня маса при сталій масі однієї хлібини;
Б) довжина і ширина прямокутника при сталій площі:
В) площа прямокутника і його довжина при сталій ширині;
Г) швидкість потягу і час для подолання ним заданої відстані;
Д) кількість пакетів і маса одного пакета при розфасуванні 10 кг борошна;
Є) площа квадрата і довжина його сторони;
Ж) вартість і кількість товару при одній і тій же ціні?
@ Під час виконання цього завдання варто звернути увагу на те, що для пошуку правильної відповіді можна скористатися таким методом: уявити, що одна з величин збільшилась у якусь кількість разів (наприклад, у 2), а потім перевірити або на інтуїтивному рівні, або використовуючи вивчені раніше формули і співвідношення, як змінилась інша величина.
Для “сильних” учнів можна надати таку інформацію: величини х і у, залежність між якими можна виразити формулою у = kх, де k – число, що не дорівнює 0; є прямо пропорційними.
Письмові вправи
1. Сталева кулька об’ємом 5 см3 має масу 39 г. Яку масу має кулька об’ємом 2,5 см3, зроблена з тієї ж сталі?
2. Зі 100 кг насіння льону виходить 37 кг олії. Скільки олії вийде із 250 кг такого насіння?
3. У 80 кг картоплі міститься 14 кг крохмалю. Скільки картоплі треба взяти, щоб одержати 35 кг крохмалю?
4. На пошиття 30 однакових костюмів пішло 99,6 м тканини. Скільки таких же костюмів вийде із 149,4 м тканини?
5. Довжина автомобільної траси 150 км. Яка довжина цієї траси на карті з масштабом 1 : 500 000?
6. На деякій ділянці залізничного шляху старі рейки завдовжки 6 м вирішили замінити новими завдовжки 9 м. Скільки потрібно нових рейок, щоб замінити 720 старих?
@ Треба пояснити учням, що задачі, які розв’язуються на цьому уроці, є схожими на ті, що їх розв’язували в темі “Знаходження дробів і відсотків від числа та числа за його дробом і відсотками” та в темі “Масштаб” (5 кл.). Але тепер ми вчимося розв’язувати ці задачі, складаючи пропорції.
V. Підсумки уроку
Щоб перевірити, чи добре засвоїли учні знання основних моментів уроку, можна запропонувати такі задачі.
1. Як знайти товщину аркуша паперу, з якого виготовлено підручник?
2. Верблюд упродовж однієї години витримує вантаж масою 200 кг. Упродовж якого часу він витримає вантаж масою 2 т? (Величини не є прямо пропорційними!)
VI. Домашнє завдання
1. Які з наступних величин є прямо пропорційними, а які обернено пропорційними?
А) Кількість хлібин та їхня маса при сталій масі однієї хлібини;
Б) довжина і ширина прямокутника при сталій площі;
В) площа прямокутника і його довжина при сталій ширині;
Г) швидкість потяга і час для подолання ним заданої відстані;
Д) кількість пакетів і маса одного пакета при розфасуванні 10 кг борошна;
Є) площа квадрата і довжина його сторони;
Ж) вартість і кількість товару при одній і тій самій ціні.
2. Сувій, в якому 42 м тканини, коштує 1302 грн. Скільки коштує сувій, в якого 36 м такої тканини?
3. Із 20 кг води озера Сиваш можна видобути 0,5 кг солі. Скільки потрібно взяти цієї води, щоб видобути 1 т солі?
4. Знайдіть відстань між двома містами, якщо відстань між ними на карті з масштабом 1 : 1 000 000 дорівнює 8, 4 см.
5. Виконайте дії:
А) 645 328 – 328 : 8 + 198 – 306;
Б) 713,4 : (61 – 26,2) + 4,8 – 3,5;
В) 4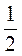 -2
-2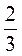 – 6
– 6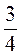 ; г)
; г) 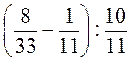 .
.
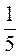 :
: ;
;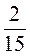 : 1 =
: 1 = 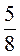 :6
:6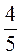 :
: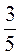
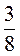 ; 3) 2
; 3) 2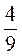 ; 3)
; 3) 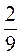 .
.