Головна ⇒ 📌Довідник з математики ⇒ Пряма та обернена пропорційність
Пряма та обернена пропорційність
Математика – Алгебра
Множення і ділення звичайних дробів
Пряма та обернена пропорційність
Дві змінні величини, відношення відповідних значень яких є сталим, називаються Прямо пропорційними.
Це означає, що при збільшенні (зменшенні) однієї величини в декілька разів у стільки ж разів збільшується (зменшується) друга величина.
Приклади прямо пропорційних величин:
1) У випадку руху з постійною швидкістю пройдена відстань прямо пропорційна витраченому часу. (Дійсно, 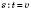 , а швидкість стала.)
, а швидкість стала.)
2)
3) Периметр квадрата з довжиною сторони а є прямо пропорційним довжині сторони, оскільки
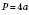 , тобто
, тобто 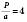 – стала величина.
– стала величина.Дві змінні величини, добуток відповідних значень яких є сталим, називаються Обернено пропорційними.
Це означає, що при збільшенні (зменшенні) однієї величини в декілька разів у стільки ж разів зменшується (збільшується) друга величина.
Приклади обернено пропорційних величин
1) Якщо пройдена відстань залишається сталою, то витрачений
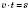 , а s – стала величина.)
, а s – стала величина.)2) Ширина і довжина прямокутника сталої площі:
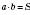 .
.3) Час, за який буде виконаний певний обсяг роботи, і кількість робітників.
Зверніть увагу на те, що число відсотків деякої величини прямо пропорційно значенню цієї величини.
Related posts:
- Пряма пропорційність. Пропорційні величини Урок № 4 2 Тема. Пряма пропорційність. Пропорційні величини Мета: сформувати уявлення учнів про пряму пропорційну залежність величин, ознайомити із прикладами таких величин, що їх учні зустрічають у повсякденному житті та під час вивчення шкільних предметів; сформувати вміння розв’язувати задачі цього типу складанням пропорції. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього […]...
- ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 14. ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ За допомогою пропорцій можна розв’язувати задачі. Ви знаєте, наприклад, що вартість товару залежить від його кількості: що більшу кількість товару купують, то більшою буде його вартість. Такі величини називають прямо пропорційними. Запамятайте! Дві величини називаються прямо пропорційними, якщо при збільшенні (зменшенні) однієї величини […]...
- Обернена пропорційна залежність Розділ 3 Відношення і пропорції §26. Обернена пропорційна залежність Нехай площа прямокутника дорівнює 36 см2, а довжина і ширина прямокутника є натуральними числами. Деякі з можливих значень довжини а і ширини b подано у таблиці. А, см 36 18 12 9 6 B, см 1 2 3 4 6 Кожного разу маємо різні значення довжини […]...
- Пряма пропорційна залежність Розділ 3 Відношення і пропорції §22. Пряма пропорційна залежність Нехай 1 кг товару коштує 8 грн. Визначимо вартість, наприклад, 2 кг, 4 кг, 5 кг, 0,5 кг, 10 кг цього товару: Кількість товару, кг 1 2 4 5 0,5 10 Вартість товару, грн 8 16 32 40 4 80 Кожного разу маємо різну вартість товару, […]...
- Задачі на пряму та обернену пропорційність – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на пряму та обернену пропорційність Задача 1. На пошиття 20 костюмів витратили 83 м тканини. Скільки таких самих костюмів вийде з 58,1 м тканини? Розв’язання Запишемо умову задачі у вигляді: Залежність між витраченою тканиною й кількістю костюмів – пряма пропорційність. (Тобто у скільки разів більше костюмів, у […]...
- ПРЯМА ПРОПОРЦІЙНІСТЬ РОЗДІЛ 4 ФУНКЦІЇ &18. ПРЯМА ПРОПОРЦІЙНІСТЬ Ви знаєте, що залежність вартості р цукерок від їх кількості т, якщо їх ціна становить 25 грн за кілограм, можна виразити формулою р = 25m, або в загальному вигляді у = kх. Така залежність є особливим випадком лінійної функції y = Kх + b, коли b = 0, a […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
- Пряма пропорційність Розв’яжіть задачі 946. 1) ні; 2) так; 3) ні; 4) ні. 947. 1) ні; 2) ні; 3) ні; 4) ні; 5) так. 948. малюнок 57. 949. 1) ні; 2) так; 3) ні. 950. 1) k = 4; 2) k = -0,7; 3) k = 2/3. 951. 1) ні; 2) так; 3) ні. 952. 1) ні; […]...
- Пряма пропорційна залежність. Розв’язування задач на пропорційний поділ Урок № 4 3 Тема. Пряма пропорційна залежність. Розв’язування задач на пропорційний поділ Мета: продовжити роботу з формування вмінь складати пропорції для розв’язування задач на пряму пропорційну залежність величин; вдосконалювати ці вміння під час розв’язування більш складних задач та задач на пропорційний поділ. Тип уроку: застосування знань та вмінь. Хід уроку I. Перевірка домашнього завдання […]...
- Обернено пропорційні величини Урок № 4 4 Тема. Обернено пропорційні величини Мета: сформувати уявлення учнів про зміст поняття обернено пропорційних величин; навчити відрізняти прямо і обернено пропорційні величини, розв’язувати обернено пропорційні величини складанням пропорції. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку I. Перевірка домашнього завдання 1. Вибіркова перевірка зошитів 2. Усні вправи 1. Обчисліть: 2. Чи можна […]...
- Закон Габбла §15.Будова Всесвіту 6. Закон Габбла У 1929 р. американський астроном Е. Габбл досліджував спектри галактик і звернув увагу на те, що лінії поглинання у всіх спектрах зміщені в червоний бік. Згідно з ефектом Допплера, це свідчить про те, що всі галактики від нас віддаляються. Крім того, за допомогою величини зміщення спектральних ліній можна визначити швидкість, […]...
- Задачі на рух – Приклади розв’язування типових завдань Математика – Алгебра Приклади розв’язування типових завдань Задачі на рух Задача. Відстань від А до В дорівнює 120 км. Відстань від А до В автомобіль проїхав зі швидкістю 40 км/год, а від В до А – зі швидкістю 60 км/год. Яка середня швидкість його руху? Розв’язання Щоб знайти середню швидкість автомобіля, треба весь шлях поділити […]...
- Поняття величини – Алгоритмізація Інформатика Алгоритмізація Поняття величини Базовим поняттям математичних і природних наук є поняття величини, що характеризує стани деякого об’єкта або явища. Значення та позначення величин. Припустимо, ми отримали деяке повідомлення N разом з відповідною йому інформацією I. Інформацію I називають значенням величини, а повідомлення N – позначенням величини. Кажуть, “позначенню N відповідає значення I”. Наприклад, “X […]...
- Задачі на знаходження четвертого пропорційного Задачі на знаходження четвертого пропорційного – Спосіб відношень – Спосіб знаходження однакової величини 1 Прокоментуй розв’язання задачі. □ 24 кг полуниць розклали порівну в 6 ящиків. Скільки потрібно таких ящиків, щоб розкласти порівну 48 кг полуниць? І спосіб 1) 24 : 6 = 4 (кг) – полуниць в 1 ящику, однакова величина. 2) 48 : […]...
- РІВНЯННЯ ГАРМОНІЧНИХ КОЛИВАНЬ – ГАРМОНІЧНІ КОЛИВАННЯ Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 1. МЕХАНІЧНІ КОЛИВАННЯ 1.2. ГАРМОНІЧНІ КОЛИВАННЯ 1.2.1. РІВНЯННЯ ГАРМОНІЧНИХ КОЛИВАНЬ При гармонічних коливаннях зміна коливальної величини з часом відбувається за законом синуса чи косинуса (рис. 2): Рис. 2 Де х – миттєве значення коливальної величини (зміщення від положення рівноваги); Хmax – максимальне значення коливальної величини […]...
- Шлях – Кінематика 5. Механіка 5.1. Кінематика 5.1.8. Шлях Шлях – довжина траєкторії, описаної тілом (матеріальною точкою) за певний проміжок часу (відстань пройдена тілом уздовж траєкторії руху). Позначається буквою s. Одиниця вимірювання – один метр (1 м). Шлях – скалярна величина....
- Деякі фізичні величини та одиниці їх вимірювання – Величини та одиниці ДОДАТОК 1. Величини та одиниці Міжнародна система одиниць (Systeme International d’Unites SI = CI) встановлює одиниці, обов’язкові для всіх фізичних і хімічних величин. Деякі фізичні величини та одиниці їх вимірювання Величина Визначення Одиниця Інші одиниці Довжина 1 Шлях s 1 м Площа S S = a ∙ b 1 м2 Об’єм V V = а […]...
- Strong>Швидкість. Час. Відстань 5. Множення і ділення багатоцифрових чисел Швидкість. Час. Відстань 763. Прочитай задачі. Про які величини йдеться у кожній задачі? Яка величина для тебе невідома? 1) Хлопчик пробіг 350 м, а дівчинка – на 35 м менше. Скільки метрів пробігла дівчинка? 2) Туристи йшли пішки 3 години, пливли на човні ще 2 години 30 хвилин. Скільки […]...
- Прості задачі з величинами: шлях, швидкість руху, час руху Прості задачі з величинами: шлях, швидкість руху, час руху S v t 1 Поясни, як ти розумієш: швидкість руху бензовоза становить 50 км/год; лижника – 4 м/с, легкового автомобіля – 90 км/год; теплохода – 45 км/год; меч-риби – 100 км/год. 2 Визнач, із якою швидкістю рухається велосипедист, якщо він щогодини проїжджає 18 км; ластівка, якщо […]...
- ВЗАЄМОДІЯ ЗАРЯДІВ. ЗАКОН КУЛОНА Фізика підготовка до ЗНО комплексне видання ЕЛЕКТРОДИНАМІКА 1. ОСНОВИ ЕЛЕКТРОСТАТИКИ 1.2. ВЗАЄМОДІЯ ЗАРЯДІВ. ЗАКОН КУЛОНА Різнойменно заряджені тіла і частинки притягуються, однойменно заряджені – відштовхуються. Закон Кулона: модуль сили електростатичної взаємодії між двома точковими зарядами q1 і q2, які містяться у вакуумі, прямо пропорційний добутку модулів їхніх зарядів і обернено пропорційний квадрату відстані r між […]...
- Деякі похідні одиниці фізичних величин системи СІ – Одиниці фізичних величин – Фізичні величини та їх вимірювання 2. Фізичні величини та їх вимірювання 2.3. Одиниці фізичних величин 2.3.2. Деякі похідні одиниці фізичних величин системи СІ Величина Одиниця Найменування Позначення Найменування Позначення Площа S Квадратний метр М2 Об’єм V Кубічний метр М3 Швидкість V Метр за секунду М/с Кутова швидкість Ю Радіан за секунду Рад/с Прискорення A Метр за секунду у квадраті М […]...
- Електрична сила. Закон Кулона 7. Електрика 7.4. Електрична сила. Закон Кулона Електрична сила – це сила, з якою електричне поле діє на внесене в нього заряджене тіло чи частину. Французький вчений Шарль Кулон встановив, що сила взаємодії заряджених нерухомих тіл, розмірами яких можна знехтувати, порівняно з відстанню між ними, прямо пропорційна значенням їхніх зарядів й обернено пропорційна квадрату відстані […]...
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- Письмове множення на одноцифрове число. Задача, обернена до задачі на суму двох добутків УРОК 4 Тема. Письмове множення на одноцифрове число. Задача, обернена до задачі на суму двох добутків Мета: повторити алгоритм письмового множення; ознайомити учнів із графічним зображенням (схемою) плану розв’язання задачі; скласти й порівняти задачу на знаходження суми добутків двох чисел та обернену до неї; розвивати логічне мислення. Обладнання: картки для обчислень, предметні малюнки. ХІД УРОКУ […]...
- Розділові знаки при цитатах – Пряма мова, непряма і невласне-пряма мова Українська мова Синтаксис Пряма мова, непряма і невласне-пряма мова Розділові знаки при цитатах 1. Цитати з вказівкою, кому вони належать, виділяються лапками. Інші розділові знаки ставляться так, як при прямій мові: “Шевченко, Пушкін, Міцкевич – люди, що втілюють дух народу з найбільшою красою, силою й повнотою”,- відзначив Максим Горький. 2. Якщо цитата наводиться з пропуском, […]...
- Видимі зоряні величини §13. Фізичні характеристики зір 2. Видимі зоряні величини Уперше термін “зоряна величина” був уведений для визначення яскравості зір грецьким астрономом Гіппархом у II ст. до н. е. Тоді астрономи вважали, що зорі розміщені на однаковій відстані від Землі, тому яскравість залежить від розмірів цих світил. Зараз ми знаємо, що зорі навіть в одному сузір’ї розташовуються […]...
- ШВИДКІСТЬ ПОШИРЕННЯ ЕЛЕКТРОМАГНІТНИХ ХВИЛЬ – ЕЛЕКТРОМАГНІТНІ ХВИЛІ Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 5. ЕЛЕКТРОМАГНІТНІ ХВИЛІ 5.2. ШВИДКІСТЬ ПОШИРЕННЯ ЕЛЕКТРОМАГНІТНИХ ХВИЛЬ Швидкість поширення електромагнітних хвиль у вакуумі: У діелектрику швидкість електромагнітної хвилі зменшується (хвиля гальмується): На межі поділу середовища з вакуумом хвиля заломлюється; абсолютний показник заломлення nc – число, що визначає, у скільки разів швидкість хвилі в середовищі […]...
- КООРДИНАТНА ПРЯМА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 22. КООРДИНАТНА ПРЯМА У п’ятому класі додатні числа і число 0 ви позначали на координатному промені (мал. 88). Продовжимо координатний промінь ОХ за його початок вліво. На добудованому промені нанесемо таку саму шкалу, як і на промені ОХ (мал. 89). Дістали координатну пряму. Точка О називається […]...
- Розв’язування типових задач ПОСІБНИК З ХІМІЇ ДЛЯ ВСТУПНИКІВ ДО ВИЩИХ НАВЧАЛЬНИХ ЗАКЛАДІВ Частина І. ЗАГАЛЬНА ХІМІЯ Розділ 4. ШВИДКІСТЬ ХІМІЧНИХ РЕАКЦІЙ. § 4.8. Розв’язування типових задач Задача 1. Реакція за температури 50° С відбувається за 2 хв 15 с. За який час закінчиться ця реакція за температури 70°С, якщо в даному температурному інтервалі температурний коефіцієнт швидкості дорівнює З? […]...
- Пряма мова – Пряма мова, непряма і невласне-пряма мова Українська мова Синтаксис Пряма мова, непряма і невласне-пряма мова В українській мові є три способи передачі чужої мови: пряма, непряма і невласне-пряма. Пряма мова Прямою називають точно передану чиюсь мову, тобто таку, що повністю зберігає лексику, синтаксис та інтонацію висловлення мовця. Пряма мова характеризується завершеністю своєї структури і обов’язково має при собі слова автора, їх […]...