Рівність трикутників
Урок № 28
Тема. Рівність трикутників
Мета: перевірити рівень засвоєння знань та сформованості вмінь учнів з теми.
Тип уроку: контроль знань, умінь.
Форма проведення: фронтальна контрольна робота.
ХІД УРОКУ
I. Організаційний момент
II. Перевірка домашнього завдання
Учитель збирає на перевірку зошити учнів із виконаною домашньою контрольною роботою.
III. Умова контрольної роботи
Варіант 1
Початковий рівень
1. Побудуйте нерівнобедрений трикутник ABC і проведіть медіану BM, висоту BH та бісектрису BL. Укажіть
Середній рівень
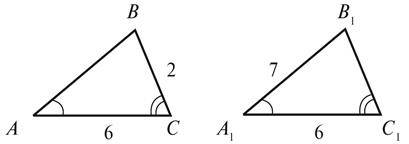
2. У трикутниках ABC і A1B1C1 (див. рис.)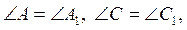 
AC=A1C1= 6 см, BC = 2 см, A1В1 = 7 см. Доведіть рівність трикутників ABC і A1B1C1 і знайдіть периметр трикутника ABC.
Достатній рівень
3. Периметр трикутника ABC дорівнює 51 см, AB =18 см, BC:AC = 5:6. Доведіть, що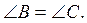 
Високий рівень
4. У трикутнику ABC висота BD ділить кут ABC навпіл. Медіана CE дорівнює 12 см. Знайдіть довжину медіани AF.
Варіант 2
Початковий рівень
1. Побудуйте нерівнобедрений трикутник LMN
Середній рівень
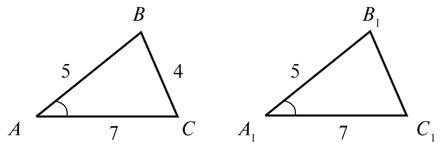
2. У трикутниках ABC і A1B1C1 (див. рис.) AB= A1B1= 5 см,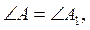 
AC= A1C1= 7 см, BC = 4 см. Доведіть рівність трикутників ABC і A1B1C1 і знайдіть периметр трикутника A1B1C1.
Достатній рівень
3. Периметр трикутника MNK дорівнює 64 см, NK = 24 см, а сторона MK в 1,5 раза менша, ніж MN. Доведіть, що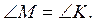 
Високий рівень
4. У трикутнику ABC медіана BD перпендикулярна до сторони AC. Бісектриса AF дорівнює 24 см. Знайдіть довжину бісектриси CE.
Варіант 3
Початковий рівень
1. Побудуйте рівнобедрений трикутник ABC з основою AC і тупим кутом B та проведіть у ньому три висоти.
Середній рівень
2. У трикутниках ABC і A1B1C1 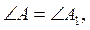сторона AB на 3 см більша, ніж AC, і на 3 см більша, ніж A1C1, а сторона AC на 3 см менша від сторони A1B1. Знайдіть периметр трикутника ABC, якщо периметр трикутника A1B1C1 дорівнює 25 см.
Достатній рівень
3. Периметр рівнобедреного трикутника дорівнює 112 см, а дві його сторони відносяться як 2 : 3. Знайдіть сторони трикутника. Скільки розв’язків має задача?
Високий рівень
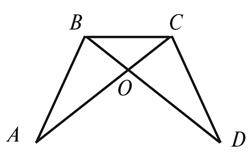
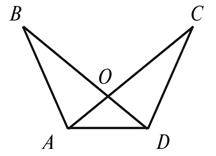
4. Дано: AB = CD, AC = BD (див. рис.). Довести: ΔBOC – рівнобедрений.
Варіант 4
Початковий рівень
1. Побудуйте прямокутний трикутник ABC з прямим кутом B і проведіть у ньому три висоти.
Середній рівень
2. У трикутниках ABC і A1B1C1 BC = B1C1, сторона AB на 2 см більша, ніж B1C1, і на 1 см більша, ніж A1C1, а A1B1 на 2 см більша від BC і на 1 см більша від AC. Знайдіть периметр трикутника ABC, якщо периметр трикутника A1B1C1 дорівнює 18 см.
Достатній рівень
3. Периметр рівнобедреного трикутника дорівнює 168 см, а одна зі сторін у 1,5 раза більше, ніж інша. Знайдіть сторони трикутника. Скільки розв’язків має задача?
Високий рівень
4. Дано: AB = CD, AC = BD (див. рис.). Довести: Δ AOD – рівнобедрений.
IV. Підсумки уроку
Підсумки можна підбити під час оголошення вчителем правильних відповідей або їх демонстрації за допомогою ТЗН.
V. Домашнє завдання
Аналіз контрольної роботи – домашня самостійна робота із розв’язаннями, що вчитель роздав учням на аркушах.
Розв’язати задачі на повторення.
1. Визначте, які з наведених тверджень правильні:
А) дві прямі, перпендикулярні до третьої, перпендикулярні;
Б) дві прямі, паралельні третій, паралельні;
В) через будь-яку точку площини можна провести пряму, паралельну даній;
Г) через будь-яку точку площини можна провести не більш ніж одну пряму, паралельну даній.
2. Через точку C, яка не належить жодній із прямих a і b, проведено пряму c. Визначте взаємне розміщення прямих b і c, якщо:
А) a||b, c||a;
Б)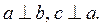 
Чи зміняться відповіді, якщо точка C лежить на прямій b?
Джерела:
1. Уроки геометрії. 7 клас./ С. П. Бабенко – Х.: Вид. група “Основа”, 2007.- 208 с.
(2 votes, average: 3.00 out of 5)
Loading...