Головна ⇒ 📌ГДЗ з математики ⇒ Рівнобедрений трикутник і його властивості

Рівнобедрений трикутник і його властивості

§ 2. Трикутники

8. Рівнобедрений трикутник і його властивості

Практичні завдання

196.

Рівнобедрений трикутник і його властивості

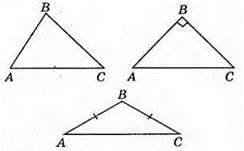
197.

Рівнобедрений трикутник і його властивості

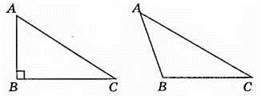
198.

Рівнобедрений трикутник і його властивості

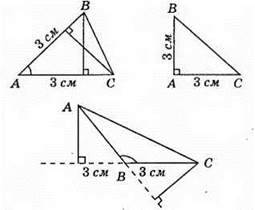
Вправи

199. 1) Р = 13 + 2 х 8 = 29(см).

Відповідь: 29 см.

2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : 2; х = 12.

Відповідь: 12 см.

200. Нехай х см – основа, тоді 10 х 2 + х = 28, тоді х = 28 – 20; х – 8.

Відповідь: 8 см.

201. Нехай х см – бічна сторона, х + 5 см – основа, тоді 2х + х + 5 – 32, звідси 3х + 5 = 32; 3х = 32 – 5; 3х = 27; х

= 27 : 3; х = 9. Отже, бічна сторона дорівнює 9 см, а основа 9 + 5 =14 (см).

Відповідь: 14 см, 9 см, 9 см.

202. Нехай х см – основа, 4х см – бічна сторона, тоді х + 4х х 2 = 54, звідси 9х = 54; х = 54 : 9; х = 6; 4х = 4 х 6 = 24. Отже, основа дорівнює 6 см, а бічна сторона 24 см.

Відповідь: 24 см, 24 см, 6 см.

203. Медіана BD є також висотою і бісектрисою, тому ∠ABD = 1/2∠ZABC = 1/2 • 100° = 50°. Оскільки ∠BCA = 40°, то ∠BAD = 40°, ∠BDA = 90°.

Рівнобедрений трикутник і його властивості

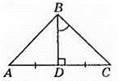
204. Оскільки BD – медіана трикутника ABC (AB = ВС), то BD – бісектриса трикутника ABC і його висота, тому ∠ABC = 2∠ABD = 2 x 53° = 106°, ∠ADE = 90°.

Відповідь: 106°, 90°.

205. Оскільки КО – висота трикутника

МКЕ (КМ = КЕ), то KD – бісектриса і медіана трикутника МЕК, тому ME = 2OЕ = 2 х 6 = 12 (см), Рівнобедрений трикутник і його властивості

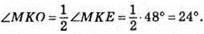
Відповідь: 12 см, 24°.

206. Оскільки? ABC – рівнобедрений, то ∠BAC = ∠BCA. Оскільки ∠1 = 140°, то ∠BAC = 180° – ∠1 = 180° – 140° = 40° (властивість суміжних кутів), ∠2 = ∠BCA = ∠BAC = 40°.

Відповідь: 40°.

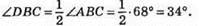
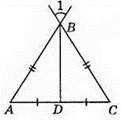
207. ∠1 = 68°, тоді ∠ABC = 68°, Рівнобедрений трикутник і його властивості

Рівнобедрений трикутник і його властивості

Відповідь: 34°.

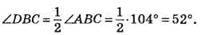
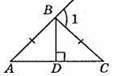
208. Рис. 179. ∠1 = 76°, тоді ∠ABC = 180° – ∠1 = 180° – 76° = 104°. Рівнобедрений трикутник і його властивості

Рівнобедрений трикутник і його властивості

Відповідь: 52°.

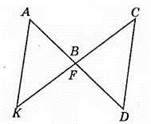
209. Оскільки? ABC і? CDE – рівнобедрені, то ∠A = ∠ACB, ∠E = ∠DCE. Крім того, ∠ACB = ∠DCE – як вертикальні. Тоді ∠A = ∠ACB = ∠DCE = ∠E. Отже, ∠A = ∠E.

210. За умовою AB = АС, тоді ∠ACB = ∠ABC (властивість рівнобедреного трикутника). Крім того, ∠ACB = ∠2, ∠ABC = ∠1 за властивістю вертикальних кутів. Toді ∠1 – ∠CBA = ∠ACB = ∠2. Отже,∠1 = ∠2.

211. ?АОВ = ?СОВ (за двома сторонами і кутом між ними: АО = СО – за умовою, ∠AOB = ∠СОВ – за у мовою, ВО – спільна сторона), тоді AВ = АС. Отже, ?ABC – рівнобедрений.

212.

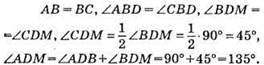
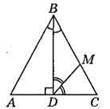
Рівнобедрений трикутник і його властивості

Рівнобедрений трикутник і його властивості

Відповідь: 135°.

213. 1) Так, обидва учні можуть бути правими, якщо даний трикутник рівносторонній.

2) Якщо трикутник – рівнобедрений, але не рівносторонній, то правий тільки перший учень.

214. Якщо AB = A1B1, то ВС = B1C1, бо трикутники АВС і А1В1С1 – рівнобедрені. Оскільки AB = А1B1, ВС = B1C1, ∠B = ∠B1, то? ABC = ?А1В1С1 за двома сторонами і кутом між ними.

Рівнобедрений трикутник і його властивості

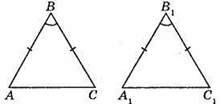
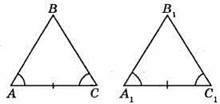
215. Якщо ∠A = ∠A1, то ∠C = ∠C1, бо трикутники АВС і А1В1С1 – рівнобедрені. Оскільки АС = A1C1, ∠A = ∠A1, ∠C = ∠C1, то? ABC = ?А1В1С1 за стороною і двома прилеглими кутами.

Рівнобедрений трикутник і його властивості

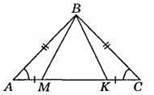
216. На рис. AB = ВС, AM = CK, ∠A = ∠C, тому? ABM = ?СВК за двома сторонами і кутом між ними. Тоді ВМ = ВК, отже, ?МВК – рівнобедрений.

Рівнобедрений трикутник і його властивості

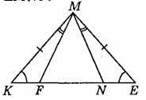
217. На рис. ME = МК, ∠E = ∠K, ∠KMF = ∠EMN, тому? KMF = ?EMN за стороною і двома прилеглими кутами. Із рівності трикутників випливає, що MF = FN, тобто? MFN – рівнобедрений, тоді∠MFN = ∠MNF.

Рівнобедрений трикутник і його властивості

218. 1) Оскільки АС = ВС, MC = КС, ∠C – спільний, то? ACM = ?ВСК.

2) Оскільки AK = АС – СК = ВС – СМ = ВМ, AB – спільна сторона, ∠KAB = ∠MBA, то? ABM = ?ВАК.

Рівнобедрений трикутник і його властивості

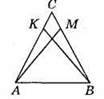
219. 1) АВ = СВ, ВМ – спільна сторона, ∠ABM = ∠CBM, тоді? AMВ = ?CMВ за двома сторонами і кутом між ними.

Рівнобедрений трикутник і його властивості

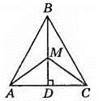
2) Оскільки AD = DC, MD – спільна сторона, ∠ADM = ∠CDM = 90°, то? AMD = ?CMD.

220. На рисунку АВ = ВС, 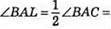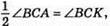Рівнобедрений трикутник і його властивостіРівнобедрений трикутник і його властивості ∠B – спільний для трикутників ABL і СВК, тоді? ABL = ?СВК за стороною і двома прилеглими кутами. Із рівності трикутників випливає, щоAL = СК.

Рівнобедрений трикутник і його властивості

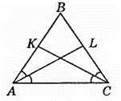
221. На рисунку AB = ВС, 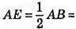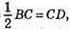Рівнобедрений трикутник і його властивостіРівнобедрений трикутник і його властивості АС – спільна сторона трикутників АЕС і CDA, ∠EAC = ∠DCA, тоді? АЕС = ?CDA за двома сторонами і кутом між ними. Із рівності трикутників випливає, що AD = СЕ.

Рівнобедрений трикутник і його властивості

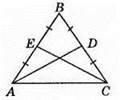
222. Оскільки ∠B = ∠C, BE = EC, 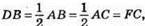Рівнобедрений трикутник і його властивості то? DBE = ?FCE. Із рівності трикутників маємо DE = EF, тобто? DEF – рівнобедрений.

Рівнобедрений трикутник і його властивості

223. Задача має два розв’язки. Якщо основа дорівнює 7 см, то бічні сторони дорівнюють 4 см; а якщо основа дорівнює 4 см, то бічні сторони дорівнюють 7 см.

Відповідь: 7 см, 4 см, 4 см або 4 см, 7 см, 7 см.

224. Якщо основа рівнобедреного трикутника дорівнює 4 см, тоді бічна сторона цього трикутника дорівнює 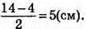Рівнобедрений трикутник і його властивості Якщо бічна сторона рівнобедреного трикутника дорівнює 4 см то основа дорівнює 14 – 4 – 4 = 6 (см).

Відповідь: 5 см, 5 см і 4 см, 6 см.

225. 1) Твердження не є правильним, бо тільки бісектриса рівнобедреного трикутника, проведена до основи, є його висотою і медіаною.

2) Твердження правильне.

3) Твердження не є правильним для трикутника зі сторонами 3 см, 5 см і 1 см. Периметр трикутника – 9 см втричі більший за сторону (3 см), проте трикутник різносторонній.

226. У трикутниках AMD, ВКМ, CDK маємо: ∠A = ∠B = ∠C, AD = ВМ = СК за умовою, AM = BK = CD – як різниці рівних відрізків AB – AM, ВС – ВК, АС – CD, тому? AMD = ?ВКМ = ?CDK. З рівності трикутників випливає: MD = KM = DK, тобто ADMК – рівносторонній.

227. У трикутниках DBK, КСЕ, EAD маємо: KB = СЕ = AD за умовою; DB = КС = АЕ – як сума рівних відрізків AD + AB, KB + ВС, АС + СЕ; ∠DBK = ∠KCB = ∠EAD – як суміжні кути до рівних кутівABC, ВСА, САВ, тому? DBK = ?КСЕ = ?EAD. Із рівності цих трикутників випливає, що DK = КЕ = DE, тобто? DEK – рівносторонній.

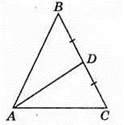
228. Нехай у рівнобедреному трикутнику AB = ВС, AD – медіана (BD = DC), АС = 20 см. Можливо два випадки:

1) P? ABD = 6 + P? ADC; 2) P? ADC = 6 + P? ABD.

1) P? ABD – P? ADC = 6, AB + AD + BD – AD – DC – AC = AB – AC, тоді AB – 20 = 6, AB = 26 (CM).

2) P? ADC – P? ABD = 6, AC + AD + DC – AD – BD – AB = AC – AB, AC – AB = 6, тоді AB = АС – 6 = 20 – 6 = 14 (CM).

Рівнобедрений трикутник і його властивості

Відповідь: 26 см або 14 CM.

Вправи для повторення

229. ∠3 = ∠1 = 35° (бо вертикальні кути рівні), ∠2 = 90° – ∠3 = 90° – 35° = 55° (бо ∠2 і ∠3 складають прямий кут), ∠4 = 180° – ∠3 = 180° – 35° = 145° (бо ∠3 і ∠4 – суміжні).

Відповідь: ∠2 = 55°, ∠3 – 35°, ∠4 = 145°.

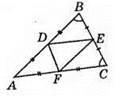
230. Нехай AB = a, DB = х, тоді CD = 2х, АС = 2 х CD = 2 х 2х = 4х.

Тоді х + 2х + 4х = а; 7х = а; х = a/7.

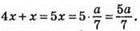
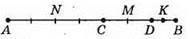
1) М – середина СD, тоді 4M = АС + СМ = Рівнобедрений трикутник і його властивості

Рівнобедрений трикутник і його властивості

Відповідь: 5a/7.

2) N і К – середини відрізків АС і DB відповідно, тоді MK = NC + CD + DK = 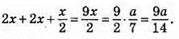Рівнобедрений трикутник і його властивості

Відповідь: 9a/14.

Спостерігайте, рисуйте, конструюйте, фантазуйте

231.

Рівнобедрений трикутник і його властивості


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  2. Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...

  3. Рівнобедрений трикутник Урок № 23 Тема. Рівнобедрений трикутник Мета: домогтися свідомого розуміння учнями понять: – умова та висновок теореми; – пряма та обернена теореми; – формулювання та доведення ознаки рівнобедреного трикутника. Сформувати вміння: – відтворювати теорему – ознаку рівнобедреного трикутника; – виділяти у формулюванні теореми умову та висновки; – використовуючи знання про пряму та обернену теореми, складати […]...

  4. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  5. Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...

  6. Трикутник і його види Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 14. Трикутник і його види З усіх многокутників трикутники мають найменшу кількість сторін. Трикутники можна розрізняти за видом їх кутів. Якщо всі кути трикутника гострі, то його називають гострокутним трикутником (рис. 117). Якщо один із кутів трикутника прямий, то його […]...

  7. Трикутник і його види Урок 40 Тема. Трикутник і його види Мета: подальше закріплення знань учнями класифікації трикутників, доповнення їх алгоритмами побудови трикутників за двома сторонами і кутом між ними та за стороною і прилеглими кутами; формування вмінь розв’язування задач на побудову і вдосконалення вмінь розв’язувати задачі на обчислення периметрів прямокутника, квадрата і трикутника. Тип уроку: застосування знань, умінь, […]...

  8. ТРИКУТНИК ТА ЙОГО ВИДИ РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ § 10. ТРИКУТНИК ТА ЙОГО ВИДИ Ви знаєте, що трикутник – це окремий вид многокутника. У нього 3 вершини, 3 сторони і 3 кути. Трикутник ABC на малюнку 119 має вершини А, В і С, сторони АВ, ВС i АС, кути ВАС, ABC і АСВ. Серед трикутників […]...

  9. Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...

  10. Трикутник та його елементи Урок № 15 Тема. Трикутник та його елементи Мета: домогтися засвоєння учнями змісту понять: “трикутник”; “сторона, вершина, кут (внутрішній) трикутника”; “кут, протилежний стороні”; “кут, прилеглий до сторони”; “периметр трикутника”; “внутрішня та зовнішня область трикутника”. Сформувати вміння: – розпізнавати та називати елементи трикутників, зображених на рисунку; – за рисунком та символічним позначенням трикутника називати кути, протилежні […]...

  11. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  12. ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ Основна ідея, якою пройнята вся математика, – це ідея рівності. Г. Спенсер РОЗДІЛ 3 ТРИКУТНИКИ У цьому розділі ви повторите свої знання про трикутники, здобуті в попередніх класах, і дізнаєтеся про багато інших їх властивостей. Основне в розділі – три ознаки рівності трикутників Вони часто використовуються в геометрії. Тому від того, як добре ви вивчите […]...

  13. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  14. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  15. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  16. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  17. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  18. Прямокутний трикутник Геометрія Основні властивості найпростіших геометричних фігур Прямокутний трикутник Трикутник називається Прямокутним, якщо він має прямий кут. Сторона, яка лежить проти прямого кута, називається Гіпотенузою. Сторони, що утворюють прямий кут, називаються Катетами. На рисунку – прямокутний. AB і BC – катети, AC – гіпотенуза. Теорема. Сума гострих кутів прямокутного трикутника дорівнює . Ознаки рівності прямокутних трикутників […]...

  19. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  20. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  21. Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...

  22. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  23. Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...

  24. Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...

  25. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  26. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  27. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  28. ПРЯМОКУТНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 16. ПРЯМОКУТНИЙ ТРИКУТНИК Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°. Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають […]...

  29. Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сто­ронами a, b і c. – формула периметра трикутника. Сума всіх кутів довіль­ного трикутника до­рів­нює . Кожний трикутник має принаймні два ­гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...

  30. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  31. Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ­ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...

  32. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  33. Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...

  34. КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...

  35. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  36. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 12. ТРИКУТНИК. СТОРОНА, ВЕРШИНА, КУТ ТРИКУТНИКА. ПОРІВНЯННЯ ПРЕДМЕТІВ (“НАЙДОВШИЙ – НАЙКОРОТШИЙ”, “ОДНАКОВІ ЗА ДОВЖИНОЮ”) Мета: ознайомити учнів із трикутником, його елементами; вчити порівнювати предмети (“найдовший – найкоротший”, “однакові за довжиною”); розвивати мислення; виховувати старанність. Хід уроку І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ […]...

  37. Вправи 325-374 325. ?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1. 1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1. ?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1. 326. […]...

  38. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  39. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  40. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

Ви зараз читаєте: Рівнобедрений трикутник і його властивості
«
»