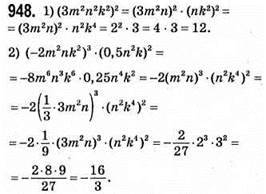Головна ⇒ 📌ГДЗ з математики ⇒ Рівняння з двома змінними

Рівняння з двома змінними

909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9).

910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння.

2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; 3) є розв’язком даного рівняння.

3) ху = 6; -2 • 3 = 6 – неправильна рівність, тому (-2; 3) не є розв’язком даного рівняння.

911. 1) х2 + 5y – 6 = 0:

(0; 1) – не є розв’язком рівняння, бо 02 + 5 • 1 – 6 = 0 – неправильна рівність;

(5; -4) – не є розв’язком рівняння, бо 52 + 5 • (-4) – 6 = 0 – неправильна рівність;

(0; 1,2) – розв’язок

рівняння, бо 0 + 5 • 1,2 – 6 = 0 – правильна рівність;

(-1; 1) – розв’язок рівняння, бо (-1)2 + 5 • 1 – 6 = 0 – правильна рівність;

(1; -1) – не є розв’язком рівняння, бо 12 + 5(-1) – 6 = 0 – неправильна рівність.

2) xy + x = 0;

(0; 1) – розв’язок рівняння, бо 0 • 1 + 0 = 0 – правильна рівність;

(5; -4) – не є розв’язком рівняння, бо 5 • (-4) + 5 ≠ 0;

(0; 1,2) – розв’язок рівняння, бо 0 • 1,2 + 0 = 0 – правильна рівність;

(-1; 1) – не є розв’язком рівняння, бо -1 • 1 + (-1) ≠ 0;

(1; -1) – розв’язок рівняння, бо 1 • (-1) + 1 = 0 – правильна рівність.

912. 2х2 – у + 1 = 0

1) А(-3; -17) – не належить графіку рівняння,

бо 2 • (-3)2 – (-17) + 1 ≠ 0;

2) В(2; 9)-належить графіку рівняння, бо 2 • 22 – 9 + 1 = 0 – правильна рівність;

3) С(-2; 9) – належить графіку рівняння, бо 2 • (-2)2 – 9 + 1 = 0 – правильна рівність.

4) D(-1; 4) – не належить графіку рівняння, бо 2 • (-1)2 – 4 + 1 ≠ 0.

913. ху – 12 = 0 не проходить через:

1) А(3;-4), бо 3 • (-4) – 12 ≠ 0;

2) В(-2; 6), бо -2 • 6 – 12 ≠ 0;

3) С(7; 2), бо 7 • 2 – 12 ≠ 0.

914. Графік рівняння:

1) 12x + 17у = 0 проходить через точку (0; 0), бо 12 • 0 + 17 • 0 = 0 – правильна рівність;

2) х2 – ху + 2 = 0 не проходить через точку (0; 0), бо 02 – 0 • 0 + 2 ≠ 0;

3) х3 – 4у = у2 + 3у проходить через точку (0; 0), бо 03 – 4 • 0 = 02 + 3 • 0 – правильна рівність.

915. 1) x – у = 10; (10; 0), (15; 5), (-15; -25) – розв’язки рівняння;

2) х = 4у; (4; 1), (16; 4), (-24; -6) – розв’язки рівняння;

3) 2х2 + у = 20; (2; 12), (-5; -30), (0; 20) – розв’язки рівняння.

916. 1) x + y = 1; (0; 1), (0,1; 0,9), (-5; 6) – розв’язки рівняння;

2) 5x – у = 2; (0; -2), (4; 18), (-9; -47) – розв’язки рівняння.

917. 4x + 3у = 30; А(6; b) належить графіку рівняння, тоді

4 • 6 + 3 • b = 30; 24 + 3b = 30; 3b = 30 – 24; 3b = 6; b = 6 : 3; b = 2; А(6; 2).

918. 7х – 5у = 47; B(а; -1); 7а – 5 • (-1) = 47; 7а = 47 – 5; 7а = 42; а = 42 : 7; а = 6; B(6; -1).

919. 1) х + у = 2.

Точка перетину з віссю х: у = 0, х = 2; (2; 0);

Точка перетину з віссю у: х = 0, у = 2; (0; 2).

2) х2 – у= 1.

Точка перетину з віссю х: у = 0, х2 = 1; х = 1 або х = -1. Таких точок дві: (1; 0) і (-1; 0).

Точка перетину з віссю у: х = 0, у = -1; (0; -1).

3) х2 + у2 = 9.

Точка перетину з віссю х: у = 0, х2 = 9; х = 3 або х = -3; (3; 0) і (-3; 6).

Точка перетину з віссю у: х = 0, у2 = 9; у = 3 або у = -3; (0; 3) і (0;-3).

4) |х| – у = 5;

Точка перетину з віссю х: у = 0, |х| = 5; х = 5 або х = -5; (5; 0) і (-5; 0).

Точка перетину з віссю у: х = 0, у = -5; (0; -5).

920. 1) 2х – 3у = 6; (0; -2) – точка перетину з віссю у, (3; 0) – точка перетину з віссю х.

2) х2 + у = 4; х = 0; у = 4; (0; 4) – точка перетину з віссю у;

У = 0, тоді х = 2 або х = -2; (2; 0) і (-2; 0) – точки перетину з віссю х.

3) |х| + |у| = 7; (0; 7) і (0; -7) – точки перетину з віссю у; (7; 0) і (-7; 0) – точки перетину з віссю х.

921. 1) х = 1, у = 2; 3х – 2у = -1; 2) х = -3, у = 5; 4х + у = -7; 3) х = 10, у = 0; 2х + у = 20.

922. 1) А(-2; 2); 3х – у = -8; 2) B(4; -1); х – 2у = 6; 3) С(0; 0); 2х – 3у = 0.

923. M(6; -3). Через точку М проходять графіки рівнянь: х – у = 9; 2х + 3у = 3; – х + 3у = -15.

924. K(0; 4). Через точку К проходять графіки рівнянь: 3х + у = 4; х + 2у = 8; 5у – 2х = 20.

925. Графіку рівняння x4 – у = -2 не належать точки, що мають від’ємну ординату, бо тоді х4 – у набувало б тільки додатний результат і х4 – у ≠ -2.

926. Графіку рівняння х + у2 = -4 не належать точки, що мають додатну абсцису, бо тоді у2 ≥ 0, х > 0. Отже, х + у2 > 0 і не дорівнювало б -4.

927. 1) у2 = х2; рівняння має розв’язки, коли у = х або у = – х;

2) у2 = – х2; має розв’язок, лише коли х = 0 і у = 0;

3) ху = 0; рівняння має розв’язки (0; у) або (х; 0); (7; 0), (0; 5);

4) х2 + у2 = 25; рівняння має розв’язки (0; 5), (-3; -4);

5) х2 + у2 = -25; не має розв’язків, бо х2 ≥ 0 і у2 ≥ 0, а – 25 < 0;

6) х2 – у2 = -9; рівняння має розв’язки, наприклад, (0; 3), (0; -3), (4; 5), (-4; 5), (4; -5);

7) |x| + |у| = 1; рівняння має розв’язки (0; 1), (0,2; -0,8);

8) |х| + |у| = 0; рівняння має розв’язок (0; 0);

9) |х| + |у| = -1; рівняння розв’язків не має, бо |х| ≥ 0, |у| ≥ 0, а – 1 < 0.

928. 1) х2 + у2 = 0; (0; 0) – розв’язок рівняння;

2) (х + 2)2 + (у – 3)2 = 0; (-2; 3) – розв’язок рівняння;

3) x4 + у6 = -4; рівняння розв’язків не має.

929. 1) х2 + (у – 2)2 = 0; (0; 2) – один розв’язок має дане рівняння;

2) (х + 3)2 + (у – 1)2 = 0; рівняння має один розв’язок (-3; 1);

3) 9х2 + 16у2 = 0; рівняння має один розв’язок (0; 0);

4) (х2 + у2)у = 0; рівняння має безліч розв’язків типу (х; 0), х – будь-яке число;

5) ху = 2; рівняння має безліч розв’язків;

6) |х + 1| + |у| = 0; рівняння має один розв’язок (-1; 0);

7) х2 + |у| = -100; рівняння не має розв’язків;

8) х + у = 2; має безліч розв’язків.

930. 1) (Х – 3)2 + (у + 4)2 = 0; 2) 7х2 + (у – 7)2 = -10; 3) х + 2у = 8; 4) 2х + у = у + 2х.

931. 1) Графік являє собою точку (1; -5);

2) графік являє собою точку (-9; 8);

3) розв’язком цього рівняння є будь-яка пара чисел, графіком є всі точки площини;

4) (х – 1)(у = 5) = 0; х = 1, у = -5. Графіком рівняння є дві прямі: х = 1 і у = -5.

932. 1) (х + 2)2 + у2 = 0; (-2; 0) – єдиний розв’язок.

Рівняння з двома змінними

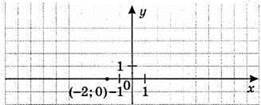
2) |х| + (у – 3)2 = 0; х = 0, у = 3; (0; 3) – розв’язок рівняння.

Рівняння з двома змінними

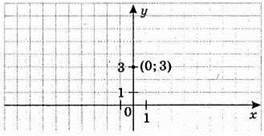
3) ху = 0; х = 0, у = 0. Графіком рівняння є сукупність двох прямих: осей координат.

Рівняння з двома змінними

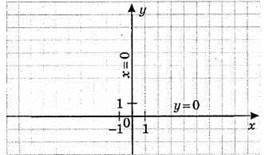
4) (х + 1)(у – 1) = 0; х = -1 або у = 1. Графіком рівняння є сукупність прямих х = -1 і у = 1.

Рівняння з двома змінними

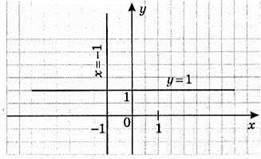
5) ху – 2у = 0; у(х – 2) = 0; у = 0 і х = 2. Графіком рівняння є сукупність прямих х = 2 та у = 0.

Рівняння з двома змінними

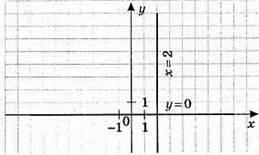
933. 1) |х – 4| + |у – 4| = 0; х = 4, у = 4; (4; 4) – єдиний розв’язок;

Рівняння з двома змінними

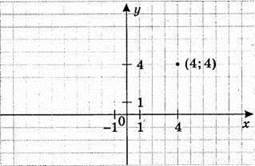
2) (х – 4)(у – 4) = 0; х = 4 або у = 4;

Рівняння з двома змінними

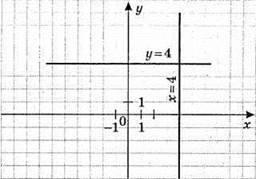
3) ху + х = 0; х(y + 1) = 0; х = 0 або у = -1. Графіком є сукупність двох прямих х = – 0 і у = -1.

Рівняння з двома змінними

934. 1) 2х + 3у = 5, (1; 1) – розв’язок рівняння;

2) х + 5у = 16, (1; 3), (6; 2), (11; 1) – розв’язки рівняння.

935. |х| + |у| = 2. (0; 2); (0; -2); (1; 1); (-1; 1); (1; -1); (-1; -1); (2; 0); (-2; 0) – розв’язки рівняння.

936. х2 + у2 – 5; (1; 2); (1; -2); (-1; 2); (-1; -2) – розв’язки рівняння.

937. 29 = 2 • 2 + 5 • 5; 29 = 2 • 7 + 5 • 3; 29 = 2 • 12 + 5 • 1.

938. 24 = 2 • 9 + 3 • 2; 24 = 2 • 6 + 3 • 4; 24 = 2 • 3 + 3 • 6.

Запропонували: 9 задач з алгебри і 2 з геометрії, або 6 задач з алгебри і 4 з геометрії, або 3 задачі з алгебри і 6 з геометрії.

939. 1) х2 + у2 + 4 = 4y; х2 + (у2 – 4у + 4) = 0; х2 + (у – 2)2 = 0; (0; 2) – розв’язок рівняння.

2) х2 + у2 + 2х – 6у + 10 = 0; (х2 + 2х + 1) + (у2 – 6y + 9) = 0; (х + 1)2 + (у – 3)2 = 0; (-1; 3) – розв’язок рівняння.

3) х2 + у2 + х + у + 0,5 = 0; (х2 + х + 0,25) + (у2 + у + 0,25) = 0; (х + 0,5)2 + (у + 0,5)2 = 0; (-0,5; -0,5) – розв’язок рівняння.

4) 9х2 + у2 + 2 = бх; 9х2 – 6х + 1 + у2 = -2; (3х – 1)2 + у2 = -2; розв’язків немає.

940. 1) х2 + 10y + 30 = 10х – у2 – 20; х2 – 10х + 25 + у2 + 10у + 25 = 0; (х – 5)2 + (y + 5)2 = 0; (5; -5) – розв’язок рівняння.

2) 4х2 + у2 + 4х = 2у – 3; 4х2 + 4х + у2 – 2у + 3 = 0; (2х + 1)2 + (y – 1)2 = -1; розв’язків немає.

941. (0; 0), (1; 0), (-1; 0); (0;-2).

Якщо х = 0, то (у2 + у)2 = у2; (у2 + у)2 – у2 = 0; (у2 + у – у)(у2 + у + у) = 0; у(у2 + 2у) = 0; у = 0 або у(у + 2) = 0; у = 0 або у = -2; (0; -2), (0; 0).

Якщо у = 0, то (х2)2 = х2; (х2 – х)(х2 + х) = 0; х2(х – 1)(х + 1) = 0; х = 0, х = 1 або х = -1; (0; 0), (1; 0), (-1; 0).

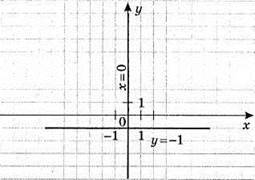
942. Точки перетину з віссю х: у = 0; 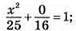Рівняння з двома змінними х2 = 25; х = 5 або х = -5; (5; 0); (-5; 0).

Точки перетину з віссю у: х = 0; y2/16 = 1; y2 = 16; у = 4 або у = -4; (0; 4); (0; -4).

Вправи для повторення

943. 1) 0,08 • 150 = 12 (мл) – кислоти в розчині;

2) 150 + 90 = 240 (мл) – утворилося розчину після доливання води;

3) 12 : 240 • 100 % = 5 % – концентрація кислоти в одержаному розчині.

944. 7 + 12 = 19 яблук червоних і жовтих разом.

Якщо витягнути 20 яблук, принаймні одне з них буде зеленим.

Рівняння з двома змінними

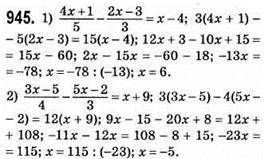
946. Нехай швидкість вантажного автомобіля х км/год, тоді швидкість легкового автомобіля 1,4х км/год.

За 3,5 год легковий автомобіль пройде 3,5 • 1,4x км, а вантажний 3,5x км. За умовою

3,5 • 1,4x – 3,5x = 77; 4,9x – 3,5x = 77; 1,4x = 77; x = 77 : 1,4; x = 55 км/год – швидкість вантажного автомобіля.

55 • 1,4 = 77 км/год – швидкість легкового автомобіля;

1,4 • 55 • 3,5 = 77 • 3,5 = 269,5 км – відстань між містами.

947. (5n + 10)2 – (2n + 4)2 = 25n2 + 100n + 100 – (4n2 + 16n + 16) = 25n2 + 100n + 100 – 4n2 – 16n – 16 = 21n2 + 84n + 84.

Оскільки n – парне, то n = 2k і тоді 21 • 4k2 + 84 • 2k + 84 = 84k2 + 84 • 2k + 84 = 84(k2 + 2k + 1) – ділиться націло на 84.

Рівняння з двома змінними


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (2 votes, average: 3.00 out of 5)
Loading...


Related posts:

  1. Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...

  2. Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...

  3. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...

  4. Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...

  5. Рівняння із двома змінними та його розв’язок Урок № 69 Тема. Рівняння із двома змінними та його розв’язок Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати […]...

  6. Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...

  7. Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...

  8. Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...

  9. Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...

  10. Рівняння із вдома змінними 870. Рівняння із двома змінними: б) x + 2у = 7; г) х – у = 1; д) 12x + 10у = 0; е) 0x – 2у = 3; ж) 3x + 0у = 0; ж) 0x + 0у = 0; з) 0x + 0y = 1. 871. 2х – у = 3. А) x […]...

  11. Лінійне рівняння з двома змінними і його графік Урок № 71 Тема. Лінійне рівняння з двома змінними і його графік Мета: вдосконалювати уміння перетворювати лінійні рівняння з двома змінними та знаходити їх розв’язки, а також будувати графіки лінійних рівнянь із двома змінними (залежно від значень а, b, с), працювати з графіками; здійснити діагностику засвоєння основних понять і вмінь, передбачених програмою за темою “Рівняння […]...

  12. Лінійне рівняння з двома змінними Розв’яжіть задачі. 1055. 1) 2; 3; -16, вільний член 16; 2) 5; -1; 12; вільний член 12; 3) 1; -2; -1; вільний член -1; 4) 5; -15; вільний член 0. 1056. 1) так; 2) ні; має тільки одну змінну у; 3) так; 4) ні; має тільки одну змінну 1057. 1) -2 – 3 + 5 […]...

  13. Система двох лінійних рівнянь із двома змінними (1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню; (2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню. 1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3). 1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5. 2 розв’язки до першого […]...

  14. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &21. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що рівняння можуть бути як з однією змінною, так і з двома змінними. Наприклад, 5(2х + у) = 15 – це рівняння з двома змінними х і у. На відміну від рівняння з однією змінною, рівняння з двома змінними може […]...

  15. Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...

  16. Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...

  17. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...

  18. Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...

  19. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...

  20. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...

  21. Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...

  22. Рівняння прямої Геометрія Декартові координати на площині Рівняння прямої Будь-яка пряма в декартових координатах x, y має рівняння виду: , де a, b, c – деякі числа. Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі “Алгебра. 8 клас” (“Лінійна функція”). Рівняння прямої, яка перетинає осі координат в точках і , […]...

  23. Лінійна функція, її графік і властивості 849. Лінійною функцією є: 850. Прямою пропорційністю є функції: 851. y = 6x – 5 X -3 -2 -1 0 1 2 3 У -23 -17 -11 -5 1 7 13 852. 1) y = -2x + 5 Якщо x = -4, то у = -2 • (-4) + 5 = 13. Якщо x = […]...

  24. Розділ 4. Функції Або немає розв’язку. 6. 1) Так; 2) ні; 3) ні; 4) так. 7. 1) -4 = -2 • (-1)2 – 3 + 1; -4 = -2 – 3 + 1; -4 = -4; А належить графіку функції; 2) 0 ≠ -2 • 12 + 3 + 1; 0 ≠ -2 + 4; 0 ≠ 2; […]...

  25. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...

  26. Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...

  27. Системи рівнянь з двома змінними УРОК 64 Тема. Системи рівнянь з двома змінними Тестові завдання 1. Яка з пар чисел є розв’язком рівняння 3х2 – 2ху +1 = 0 ? А) (1; 2); б) (2; 2); в) (0; 3); г) (0;0)? 2. Яка з пар чисел є розв’язком системи А) (3; 0); б) (2; 1); в) (1; 2); г) (0; […]...

  28. Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...

  29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...

  30. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...

  31. Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  32. Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  33. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...

  34. Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...

  35. Розв’язування систем рівнянь з двома змінними УРОК № 33 Тема. Розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про різні способи розв’язування систем рівнянь з двома змінними та випадки їх застосування. Закріпити вміння: за видом системи визначати оптимальний спосіб її розв’язування, описувати дії відповідно до обраного способу розв’язування системи рівнянь з двома змінними, а також виконувати дії відповідно […]...

  36. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...

  37. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...

  38. Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...

  39. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &24. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, що систему лінійних рівнянь із двома змінними можна розв’язати графічно. Проте існують інші, більш точні способи розв’язування таких систем – аналітичні способи. У цьому параграфі ви дізнаєтесь про два з них. До аналітичних способів розв’язування […]...

  40. Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...

Ви зараз читаєте: Рівняння з двома змінними
«
»