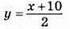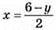Розділ 5. Лінійні рівняння та їх системи
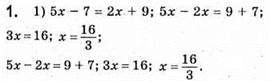
Рівносильні, бо корені однакові.
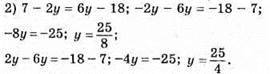
Не рівносильні, бо корені різні.
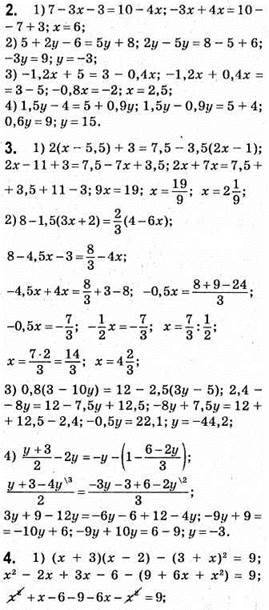
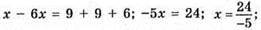
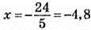 – один корінь;
– один корінь;
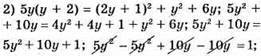
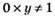 – коренів немає.
– коренів немає.
5. Нехай у 7-Б класі навчається х учнів, тоді у 7-А класі навчається (х + 3) учнів. Оскільки загальна кількість учнів у 7-А та 7-Б дорівнює 55, складемо та розв’яжемо рівняння:
Х + х + 3 = 55; 2х = 55 – 3; 2х = 52; х = 26 – учнів у 7-Б класі.
26 + 3 = 29 учнів
7. Нехай одна сторона прямокутника х см, тоді друга – 3х см. За формулою периметра прямокутника:
(х + 3х) • 2 = 24; 4х = 12; х = 3 см – менша сторона; 3 • 3 = 9 см – більша сторона.
8. Нехай швидкість першого автобуса х км/год, тоді швидкість другого (х + 5) км/год. Перший автомобіль за 3 години проїхав 3х км, а другий – 3(х + 5) км. Разом вони проїхали 390 км.
3х + 3(х + 5) = 390; 3х + 3х + 15 = 390; 6х = 390 – 15; х = 62,5 км/год – швидкість першого автобуса; 62,5 + 5 = 67,5 км/год – швидкість другого автобуса.
9. х – І число, х + 1 – ІІ число, х + 2 – III число.
Х + х + 1 + х + 2 = 906; 3х = 906 – 3; 3х = 903; х = 301 – І число;
301 + 1 = 302 –
Відповідь: 301, 302, 303.
10.
Лінійне рівняння з двома змінними | Х – у + 7 = 0 | 2х + y – 6 = 0 | Х – 2у + 10 = 0 |
Виразити у через х | -у = – х – 7 Y = х + 7 | У = 6 – 2x | -2у = 10 – х
|
Виразити х через у | Х = у – 7 |
| Х = 2у – 10 |
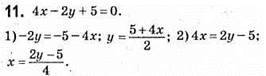
Перший розв’язок: (0; 2,5). Другий розв’язок: (-5/4; 0).
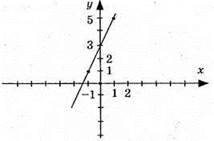
12. 1) 2х – у + 3 = 0; – у = -3 – 2х; у = 3 + 2х
X | -1 | 0 | 1 |
У | 1 | 3 | 5 |
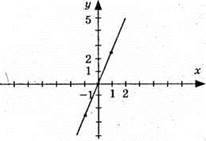
2) 5x – 2у = 0; 2у = 5х; у = 5/2х; у = 2,5х
X | -1 | 0 | 1 |
У | -2,5 | 0 | 2,5 |
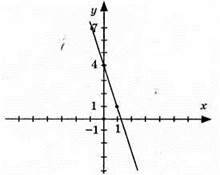
3) -3х – у + 4 = 0; – у = 3х – 4; у = 4 – 3x
X | -1 | 0 | 1 |
Y | 7 | 4 | 1 |
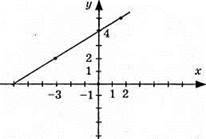
4) – x + 2y – 8 = 0; 2y = x + 8; 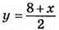
X | -2 | 0 | 2 |
Y | 3 | 4 | 5 |
13. 1) x + 2у + 2 = 0; 2) 2х – у + 5 = 0; 3) 2x – у + 3 = 0.
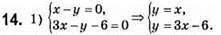
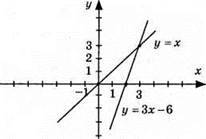
Відповідь: А(3; 3).
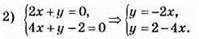
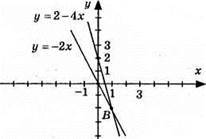
Відповідь: B(1; -2).
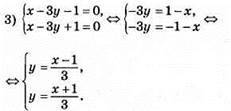
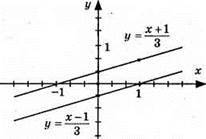
Відповідь: розв’язків немає.
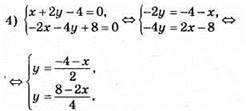
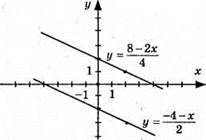
Відповідь: розв’язків немає.
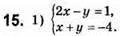 Методом додавання:
Методом додавання:
3x = -3; x = -1; 3 • (-1) – у = 1; -3 – у = 1; – у = 3; у = -3.
Відповідь: (-1; -3).
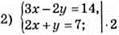 Методом додавання:
Методом додавання:
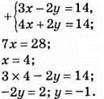
Відповідь: (4; -1).
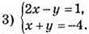 Методом додавання:
Методом додавання:
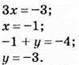
Відповідь: (-1; -3).
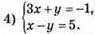 Методом додавання:
Методом додавання:
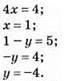
Відповідь: (1; -4).
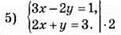 Методом додавання:
Методом додавання:
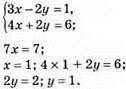
Відповідь: (1; 1).
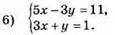 Методом додавання:
Методом додавання:
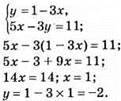
Відповідь: (1; -2).
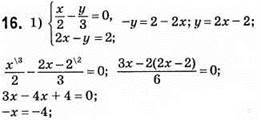
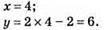
Відповідь: (4; 6).
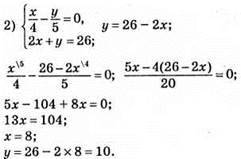
Відповідь: (8; 10).
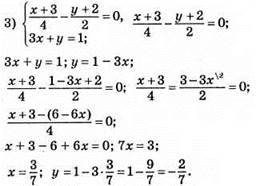
Відповідь: (3/7; -2/7).
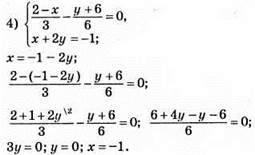
Відповідь: (-1; 0).
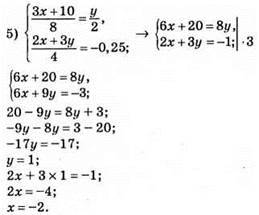
Відповідь: (-2; 1).
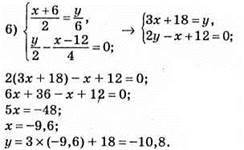
Відповідь: (-9,6; -10,8).
17. x – І число, у – II число.
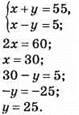
Відповідь: І число = 30, II число = 25.
18. х – І число, х + 10 – II число,
Х + х + 10 = 100;
2х + 10 = 100;
2х = 90;
Х = 45 – І число;
45 + 10 = 55 – II число.
19. х – І число, 4х – II число.
4х – х = 15;
3х = 15;
Х = 5 – І число,
5 • 4 = 20 – II число.
20. x – І число, у – II число.
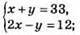
3х = 45;
У = 15 – II число;
Х + 15 = 33;
Х = 18 – І число.
21. х – І число, у – II число.
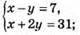
-3у = -24;
У = 8 – II число;
Х – 8 = 7;
Х = 15 – І число.
22. х – І число, у – II число.
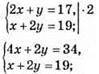
3х = 15;
Х = 5 – І число;
2 • 5 + у = 17;
У = 7 – II число.
23. х – І число, у – II число,
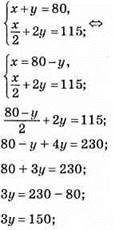
У = 50 – II число;
Х = 80 – 50 = 30 – І число.
24. х – чисельник, у – знаменник.
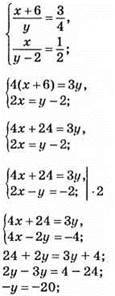
У = 20 – знаменник;
4х – 24 = 3 • 20;
4х = 60 + 24;
4х = 84;
Х = 21 – чисельник.
Дріб: 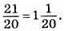
25. х – чисельник, у – знаменник.
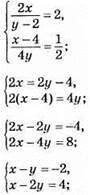
Y = -6 – знаменник:
Х = -8 – чисельник.
Дріб: 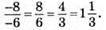
26. х грн – коштує 1 кг печива;
(х + 13) грн – коштує 1 кг цукерок.
5х грн – заплатили за 5 кг печива;
3(х + 13) грн – заплатили за 3 кг цукерок.
5х + 3(х + 13) = 135;
5х + 3х + 39 = 135;
8х = 135 – 39;
8x = 96;
Х = 12 грн – коштує 1 кг печива.
27. х км/год – швидкість вантажного автомобіля;
(х + 30) км/год – швидкість легкового автомобіля;
3,5 • (х + 30) км – проїхав легковий автомобіль;
5 • х км – проїхав вантажний автомобіль.
3,5 • (х + 30) = 5х;
3,5х + 105 = 5х;
3,5х – 5х = -105;
-1,5х = -105;
Х = 70 км/год – швидкість вантажного автомобіля;
70 + 30 = 100 км/год – швидкість легкового авто.
28. х км/год – швидкість першого авто; у км/год – швидкість другого авто.
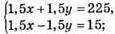
3у = 210;
У = 70 км/год – швидкість II авто;
1,5х – 1,5 • 70 = 15;
1,5х = 15 + 1,5 • 70;
Х = 80 км/год – швидкість І авто.
29. Нехай х – відстань між пунктами А і В, тоді
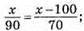
20х = 9000;
Х = 450 (км) – відстань між містами.
30. х – швидкість катера; у – швидкість течії.
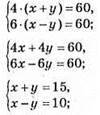
2х = 25;
Х = 12,5 – швидкість катера;
У + 12,5 = 15;
У = 2,5 – швидкість течії річки.
31. х – швидкість човна; у – швидкість течії річки.
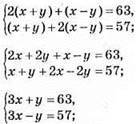
6х = 120;
Х = 20 км/год – швидкість човна;
3 • 20 + y = 63;
60 + у = 63;
У = 3 км/год – швидкість течії річки.
32. х років батькові, у років доньці.
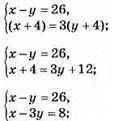
2у= 18;
У = 9 – років доньці;
Х = 35 – років батькові.