Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Розкладання багаточленів на множники винесенням спільного множника за дужки

Розкладання багаточленів на множники винесенням спільного множника за дужки

Урок № 38

Тема. Розкладання багаточленів на множники винесенням спільного множника за дужки

Мета: відпрацювати навички розкладання багаточленів на множники винесенням спільного множника за дужки; удосконалити вміння застосовувати винесення спільного множника за дужки.

Тип уроку: застосування знань, умінь та навичок.

Хід уроку

I. Перевірка домашнього завдання

Математичний диктант

Варіант 1 [2]

1. Який степінь множника а [b] можна винести за дужки в багаточлені

A2x – a5x3 [ab2 – a3b5]?

2. Який числовий множник можна

винести за дужки в багаточлені

12х3 – 8х2 [15а3 – 25а]?

3. Винесіть за дужки спільний множник усіх членів багаточлена

A2 + ab – a [х2 – ху – х].

4. Подайте у вигляді добутку 12а2х – 8а5х3 [15ab2 – 25a3b5].

@ Після виконання завдань математичного диктанту учні виконують самоперевірку за зразками правильних розв’язань, підготовлених учителем або “сильними” учнями, які працювали, наприклад, за відкидною дошкою, після чого, в разі необхідності, здійснюємо корекцію (робота в парах).

II. Актуалізація опорних знань

Бесіда

1. Яке перетворення називається розкладанням багаточлена на множники?

На прикладі виразу 2ху – 6х2 поясніть, як виконується розкладання багаточлена на множники винесенням спільного множника за дужки.

3. Укажіть спільний множник у виразах:

1) 2х + 6;

2) 8х – 12у;

3) bab + a;

4) х2 – х;

5) а3 – 2а4 – 3а5;

6) х2 + ху;

7) 0,2 • 7 – 0,8 • 7;

8) 0,22 + 0,23;

9) 65 + 35 + 1352.

III. Робота з випереджальним домашнім завданням

Завдання. Вкажіть множники у виразах. Знайдіть та виділіть спільні множники:

1) 2а(х + у) + b(х + у);

2) у(а – b) – 2(а – b);

3) 3а(с + 3) – х(с + 3);

4) 9(р – 1) – (р – 1)2;

5) (а + 3)2 – а(а + 3);

6) (а + 3) – а(а + 3).

@ Учні самостійно виконали це завдання вдома і, мабуть, після цього мають міркування щодо перетворення поданих виразів. Тому єдине, що їм треба – закінчити логічний ланцюжок: у виразі є спільний множник > спільний множник можна винести за дужки > вираз, що залишається в дужках, є алгебраїчною сумою “неспільних множників”.

По цьому пропонуємо учням самостійно виконати завдання з винесення спільного множника за дужки, а далі перевіряємо, аргументуємо та корегуємо виконані завдання (можна організувати роботу в малих групах, призначивши консультантами тих учнів, які впорались із завданням бездоганно). Звертаємо увагу, що перетворення виразу ab + ac y добуток можливе й за умови, що а не є одночленом.

IV. Застосування навичок

Мотивація

@ Звернемо увагу учнів, що задача № 3 (див. попередній урок) ще не розв’язана. Тому пропонуємо попрацювати спочатку над подібним завданням, а потім уже виконаємо вправи традиційного змісту достатнього та високого рівня складності.

Виконання письмових вправ

1. Доведіть, що значення виразу:

1) 165 + 164 ділиться на 17;

2) 389 – 388 ділиться на 37;

3) 365 – 69 ділиться на 30;

4) 518 – 258 ділиться на 120.

2. Доведіть, що:

1) 78 – 77 + 76 ділиться на 43;

2) 213 – 210 – 29 ділиться на 13;

3) 274 – 95 + 39 ділиться на 25;

4)164 – 213 – 45 ділиться на 11.

@ Важливо, щоб учні усвідомили, що перетворення суми степенів неможливо (без обчислень) здійснити іншим шляхом, окрім розкладання на множники (ще раз підкреслити, що відповідної властивості степеня не існує!)

3. Розкладіть на множники:

1) х(а + b)+ у(а + b);

2) а(3х – 2у)+ b(3х – 2у);

3) 3х(а – b) – 5у(b – а);

4) 2у(n – m) + (m – n);

5)(х + 3)2 – 3(х+3);

6) (х + 3)(2у – 1) – (х + 3)(3у + 2).

4. Доведіть тотожність:

1) (2х – 7у)(3х2 + 5ху – 2у2) – (2х – 7у)(3х2 + 2ху – 2у2) = 3ху(2х – 7у);

2) (3m – 4)(7n2 – 3n – 5) + (4 – 3m)(7n2 – 3n – 3) = 8 – 6m.

@ 3 метою усвідомлення необхідності виробити вміння та навички розкладання багаточленів на множники в завданні 4 можна запропонувати виконати доведення спочатку без використання алгоритму винесення спільного множника за дужки, а потім із його використанням. Розбіжність буде вражаючою.

5*. Права частина даних рівностей утворена з лівої після винесення за дужки деякого числового коефіцієнту. Знайдіть ці коефіцієнти та підставте замість (*):

1) 2a + 4b = *(a + 2b);

2) 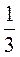A – 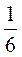B + c = *(2a – b + 6c);

3) 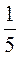T + 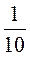И – 1 = *(2t + и – 10);

4) а2 – 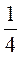B2 = *(b2 – 4а2).

6*. Логічні вправи.

Знайдіть та підставте пропущені слова, числа, букви:

Сухар	27а5b7
Уха	?
Муха	18а8b2с

V. Підсумки уроку

VI. Домашнє завдання

№ 1. Розкладіть на множники:

1) 8m(а – 3) + n(а – 3);

2)(р2 – 5) – q(p2 – 5);

3) х(у – 9) + у(9 – у);

4) 7(с + 2) + (с + 2);

5) (а – b) – с(b – а);

6) – (х +2у) – 4(х + 2у).

№ 2. Розкладіть на множники ліву частину рівняння та розв’яжіть рівняння:

1) 4t3 + t2 = 0;

2) 2а2 – 5а = 0;

3) (v – 7) + v(v – 7) = 0.

№ 3. Якою цифрою закінчується вираз: 92007 + 92006 ?

№ 4. Випереджальне домашнє завдання. Дано два набори двочленів. Для кожного двочлена з першого набору знайти відповідний двочлен із другого набору, щоб після винесення в кожному з них спільного множника за дужки в дужках залишились однакові багаточлени. Покажіть цю відповідність стрілками.

І набір:

1) 2x – x2; 2) ab – 3b2; 3) n2 – mn;

II набір:

1) mn – m2; 2) 2а b – 2b2; 3) 5 + 10х;

4) 4х – 8; 5) 6а2 – 9ab; 6) -5 – 10x;

4) 4ху – 2х2у; 5) х2 – 2х; 6) а2 – 3аb;

7) -3ax + 2х2

7) -3а2 + 2ах