РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ
РОЗДІЛ 3 МНОГОЧЛЕНИ
&14. РОЗКЛАДАННЯ МНОГОЧЛЕНІВ НА МНОЖНИКИ
Ви вже знаєте, як розгорнути в многочлен добуток многочленів. Нерідко виникає потреба виконати обернену дію – згорнути многочлен у добуток кількох множників. Таку дію називають розкладанням многочлена на множники.
Запам’ятайте!
Розкласти многочлен на МНОЖНИКИ – означає перетворити його в добуток кількох виразів.
Для розкладання многочлена на множники застосовують різні способи. Розглянемо їх.
1. Винесення спільного множника за дужки
Задача
-6x5y7 – 24х4у3 + 6х2у4.
Розв’язання. 1. Визначимо коефіцієнт спільного множника членів даного многочлена. Для цього спочатку знайдемо НСД чисел 6, 24 і 8. Він дорівнює 2. Оскільки коефіцієнт першого члена від’ємний, то зручно за коефіцієнт спільного множника взяти число -2.
2. Визначимо буквену частину спільного множника членів даного многочлена. Кожен член многочлена містить: а) степені змінної х, найнижчим з яких є другий степінь; б) степені змінної у, найнижчим з яких є третій степінь. Тому буквеною частиною спільного множника є вираз х2у3.
3. Винесемо спільний множник
-6х5y7 – 24х4y3 + 8х2y4=
=-2х2y3(3х3y4 +12х2 – 4у).
Зверніть увагу:
Щоб перевірити, чи правильно виконали винесення спільного множника за дужки, виконайте обернену дію, тобто розкрийте дужки.
2. Застосування формул скороченого множення
За формулами скороченого множення можна відразу подати у вигляді добутку особливі многочлени, такі як повний квадрат суми чи різниці, різниця квадратів, сума і різниця кубів. Для цього застосовують такі формули:
А3 + 2ab + b2 = (а + b)2= (а + b)(a + b),
A2 – 2ab + b2 = (a – b)2 = (a – b)(a – b),
A2 – b2 = (a + b)(а – b),
A3 + b3= (a + b)(a2 – ab + b2),
А3 – b3 = (a – b)(a2 + аb + b2).
Розглянемо, як можна застосувати формули скороченого множення в більш складних випадках.
Задача 2. Розкладіть на множники двочлен 16х4y6 – х2y4.
Розв’язання. Задачу можна розв’язати двома способами.
Спосіб 1. Оскільки обидва члени даного двочлена містять змінні х і у в парних степенях і коефіцієнт першого члена 16 = 42, тo кожен доданок можна подати як квадрат деякого одночлена:
16х4у6 – х2y4 =
= (4x2y3)2 – (ху2)2.
Дістали різницю квадратів одночленів, яку можна розкласти на множники за відповідною формулою:
(4х2y3)2 – (ху2)2=
= (4х2y3 + ху2)(4x2y3 – xy2)
І в перших, і в других дужках міститься двочлен, який ще можна розкласти на множники, винісши за дужки спільний множник. Тоді дістанемо:
(4х2у3+ ху2)(4х2у3 – ху2) =
= ху2(4ху + 1) ∙ ху2(4хy – 1) =
= х2у4(4ху +1)(4ху – 1).
Спосіб 2. У даному двочлені 16х4у6 – х2y4 спочатку винесемо за дужки спільний множник, а потім вираз у дужках розкладемо на множники за формулою різниці квадратів:
16х4y6 – х2y4 =
= х2y4(16х2у2 – 1) =
= х2y4(4хy + 1)(4ху-1).
Зверніть увагу:
Якщо спочатку винести спільний множник за дужки, то застосовувати формули скороченого множення буде легше.
3. Спосіб групування
Якщо многочлен містить більш як три члени, то застосовують спосіб групування.
Задача 3. Розкладіть на множники многочлен:
2х2 – х + 2ху – у.
Розв’язання. Згрупуємо доданки так: перший – із другим, а третій – із четвертим У кожному з цих двочленів винесемо спільний множник за дужки:
2х2 – х + 2ху – у =
= (2х2 – х) + (2ху – у) =
= х(2х – 1) + у(2х – 1).
Отримали вираз, кожен доданок якого містить спільний множник 2х – 1. Винесемо цей спільний множник за дужки:
Х(2х – 1) + у(2х – 1) =
= (2х – 1)(х + у).
Отже, 2х2 – х + 2ху – у = (2х – 1)(х + у).
? Чи можна в многочлені з чотирма членами згрупувати доданки по-іншому: перший – із третім, а другий – із четвертим? Так. Переконайтеся в цьому самостійно на прикладі многочлена, який дано в задачі 3.
Зверніть увагу:
Групуючи члени многочлена, будьте уважними щодо знаків:
– якщо за дужки виносите множник зі знаком “+”, то знаки всіх членів у дужках залишайте без змін;
– якщо за дужки виносите множник зі знаком “-” , то знаки всіх членів у дужках змінюйте на протилежні.
Дізнайтеся більше
Калужнін Лев Аркадійович (1914- 1990) – видатний український математик-алгебраїст, доктор фізико-математичних наук, професор.
У 1923 мати з 9-річним Львом емігрували до Німеччини, де він закінчив реальне училище, навчався спочатку в Берлінському, а потім у Гамбурзькому університетах. У 1938 Лев Аркадійович переїхав до Франції, де слухав лекції у Сорбонні.
З 1946 працював в Інституті вищих наукових досліджень Паризької академії наук, де в 1948 захистив докторську дисертацію. У 1951-1955 – професор Берлінського університету. З 1955 працював в Київському університеті (професор кафедри математичного аналізу, теорії ймовірностей та алгебри). У 1957 Л. А. Калужнін захистив докторську дисертацію вже в Україні. У 1959-1970 – завідувач кафедри алгебри та математичної логіки, у 1970-1986 – професор цієї кафедри. Є автором понад 130 наукових та науково – методичних праць. Створив потужну наукову школу. Серед його учнів – 18 кандидатів та 4 доктори наук. Наукові дослідження належать до різних розділів алгебри і дискретної математики, але найвагоміші результати стосуються теорії груп.

ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що означає – розкласти многочлен на множники?
2. Які способи розкладання многочлена на множники ви знаєте?
3. Як перевірити, чи правильно виконали винесення спільного множника за дужки?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
702. Укажіть правильне завершення твердження: “Розкласти многочлен на множники – означає…”:
1) замінити в многочлені знаки “+”і”-” на знак множення;
2) перетворити його в суму двох виразів;
3) розставити дужки в многочлені;
4) перетворити його в добуток кількох виразів.
703. Чи правильно винесено спільний множник за дужки:
1) 2а + 6b = 2(а + b); 3) 2a + 6b = 2(а +3b)?
2) 2а + 6b = 2(а + 2b);
704. Чи правильно винесено спільний множник за дужки:
1) аb + bc = a(b + c); 3 )ab + bс = с(a + b)?
2) ab + bc = b(a + c);
705. Чи правильно розкладено вираз на множники:
1) 9 – b2 = (9 + b)(9 – b); 3) 9 – b2 = (3 – b)(3 + b)?
2) 9 – b2 = (3 – b)(3 – b);
706. Чи правильно розкладено вираз на множники:
1)с2 – b2 = (с – b)(с – b); 3) с2 – b2 = (с – b)(с + b)?
2) с2 – b2 = (b – с)(с – Ь);
707. Чи правильно розкладено вираз на множники:
1) а3 – d3 = (a – d)(a2 – ad + d2);
2) a3 – d3 = (a – d)(a2 + ad + d2);
3) a3 – d3 = (a – d)(a2 + 2ad + d2)?
708. Чи правильно розкладено вираз на множники:
1) t3 – 1 = (t – 1)(t2 – t + 1); 3) t3 – 1 = (t – 1)(t2 + t + 1)?
2) t3 – 1 = (t – 1)(t2 + 2t + 1);
709. Чи правильно, що 2х2 + 8х дорівнює:
1) 2х(х + 8);
2) 2х(х2+ 4);
3) 2х(х + 4)?
710. Чи правильно, що 6х2 + 2х + 10х3 дорівнює:
1) 2х(4х + 1 + 5х2); 3) 2х(3х +1 + 5х2)?
2) 2х(2х + 2 + 5х2);
711. Чи правильно, що 4х2 – 9 дорівнює:
1)(2х – 3)(2х + 3); 3) (2х – 3)(2х – 3)?
2) (2х2 – 3)(2х2 + 3);
712. Чи правильно, що а3 – 8 дорівнює:
1) (а – 4)(а2 – а + 2); 3) (а -2)(а2 + 2а + 4)?
2) (а – 2)(а2 – а + 4);
713. Чи правильно, що х3 – 3х2 + 2х – 6 дорівнює:
1) (х – 3)(2х2 – 6);
2) (х – 3)(х2 + 2);
3) (2х – 6)(х2 + 1)?
714. Чи правильно, що а3 – 2a2 + 2а – 4 дорівнює:
1) (а + 2)(а2 – 2);
2) (а – 1)(а2 + 4);
3) (а – 2)(а2 + 2)?
715. Який із наступних виразів дорівнює виразу 25а2 + 35:
1) 5(5а2 + 6);
2) 25(а2 + 10);
3) 5(5а2 + 7)?
716. Який із наступних виразів дорівнює виразу 9х4 + 12х3:
1)3х3(3х2 + 4);
2)3х3(3х + 4);
3)4х3(3х + 4)?
717. Який із наступних виразів дорівнює виразу х4у6 + х3у4:
1) х4y4(y2 + 1);
2) х3y4(xy2 +1);
3)х3у4(ху + 1)?
718. Яка з наступних рівностей є тотожністю:
1) 3х3у2 + 6х3у5 = Зх3у2(1 + у2);
2) 3x3y2 + 6x3y5 = 3x3y2(1 + 2y2);
3) 3х3у2 + 6х3у5 = 3х3у2(у2 + 2)?
719. Яка з наступних рівностей є тотожністю:
1) 12xz2 + 8x3z2 = 4xz2(4 + 2х2);
2) 12хz2 + 8x3z2 = 2xz2(6 + 4х2);
3) 12хz2 + 8x3z2 = 4xz2(3 + 2х2)?
720. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) 2а2 + 4а3 + 6а4 =* ∙ (1 + 2a + 3а2);
2) 9b3 + 12b2 + 18b5 = 3b2(3b + * + 6b3);
3) 25a2b2 + 40а3b3 + 65a5b5 = * ∙ (5 + 8ab + 13а3b3);
4) 19b3с3 + 38b2c5 + 1 = 19b2с3(b + * + с).
721. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) 15n2 + 10n7 + 35n3 = * ∙ (3 + 2n5 + 7n);
2) 42m5n4 + 49m4n5 + 35m3n3 = * ∙ (6m2n + 7mn2 + 5).
722. Розкладіть на множники многочлен способом винесення спільного множника за дужки:
1) 2m2 + 4m + 6m3; 3) 0,4а3 + 1,6а5 + 0,8а2.
2) 6n4 + 9n6 + 12n3;
723. Розкладіть на множники многочлен способом винесення спільного множника за дужки:
1) 12b5 + 24b3 + 6b2; 3) 1,5d3 + 2d6 + 3d8.
2) 36с4 + 18с7+ 27с3;
724. Розкладіть на множники многочлен способом винесення спільного множника за дужки:
1) a3b + ab3+ a2b2;
2) a4b3 + a3b4+ а2b2;
3) a2b3 + a3b2 + a4b4.
725. Розкладіть на множники вираз способом винесення спільного множника за дужки:
1) х (y + 4) – y (4 + у); 3)b(3b + 5) – 9b – 15.
2) 2m(n2 – 1) – 3n(1 – n2);
726. Розкладіть на множники вираз способом винесення спільного множника за дужки:
1) a(5b + 6)- b(6 + 5b); 3)у(2у +1) – 4у – 2.
2) 7(m3 – 2) – 5m(2 – m3);
727. Який із наступних виразів дорівнює виразу 1 – 16b2:
1)(4b -1)(1 + 4b); 2)(1 – 16b)(1 + 16 ); 3) (1 – 4b)(4b + 1)?
728. Який із наступних виразів дорівнює виразу 9х4 – 16:
1) (3х2 + 16)(3х2 – 16); 3) (3х – 4)(3х + 4)?
2) (3х2 + 4)(3х2 – 4);
729. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1) 25m2 – 4; 2) 9 – 36n4; 3) 0,04а4 – 0,81.
730. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1)64 – 25а2; 2) 16b2 – 9; 3) 0,49а4 – 0,04.
731. Уставте замість зірочок такий одночлен, щоб утворилася тотожність:
1) 4а2 – 25b2 = (* – 5b)(* + 5b);
2) 81х2y4 – 16а6 = (* – 4а3)(* + 4а3);
3)  С2d4 – 0,16а2 = (* – 0,4а)(* + 0,4а).
С2d4 – 0,16а2 = (* – 0,4а)(* + 0,4а).
732. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1) а2b6 – 25; 2)b12с4 – 36; 3) х4y2 – 0,81.
733. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1) 4m2n2 – 1; 2) b10c6 – 16; 3)х8y4 – 0,36.
734. Чи правильно, що 4x2y2 – у4 дорівнює:
1) (2хy – у2)(2ху + а2); 3) (2ху – у4)(2ху + у4)?
2) (2х2y2 – y2)(2x2y + у2);
735. Який із наступних виразів дорівнює виразу х4у6 – х6у4:
1) (х2у3 – х3у2)(x2у3 + х3у2); 3) (х3y2 – х2у3)(х2y3 + х3y2)?
2) (x2y2 – x3y3)(x2y2 + х3y3);
736. Уставте замість зірочки такий двочлен, щоб утворилася тотожність:
1)а6 – 16а4 = (*) ∙ (а3 + 4а2); 3) 100n2 – 81m8=(*) – (10n – 9m4).
2)9b6 – 36b2 = (3b3 – 6b) ∙ (*);
737. Уставте замість зірочки такий двочлен, щоб утворилася тотожність:
1) а4 – 4а8 = (*) ∙ (а2+ 2а4);
2) 49b2 – 36b10 = (7b – 6b5) ∙ (*);
3) 121n6 – 64m12 = (*) ∙ (11n3 – 8m6).
738. Чи правильно, що 27х3 + 8 дорівнює:
1) (3х + 2)(9х2 – 12х2 + 4); 3) (3х – 2)(9х2 + 6х2 + 4)?
2) (3х + 2)(9х2 – 6х + 4);
У неправильних рівностях укажіть, де допущено помилку.
739. Який із наступних виразів дорівнює виразу 27х6 – 125:
1) (3х2 – 5) (9х4 – 15х2 + 25); 3) (3х2 – 5)(9х4 + 15х2 + 25)?
2) (3х2 – 5)(9х4 + 15х + 25);
740. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1)8а6 – 27; 2)b12 + 64; 3) 0,125×3 – 1.
741. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1) b6 + 125; 2) а12 – 0,001; 3)216 – х9.
742. Чи правильно, що 216х3 + 8у6 дорівнює:
1) (6х + 2Y2)(36Х2 – 24 ху2 + 4 у2);
2) (6х + 2Y2)(36Х2 – 12хy2 + 4y4);
3) (6х + 2у2)(6х2 – 12ху + 2у )?
У неправильних рівностях укажіть, де допущено помилку.
743. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1)a2b6 – a4b8; 2) a12b3 – a6b6; 3)a3b3 + a6b6.
744. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1) 4m2n6p4 -16; 2) 27a3b6 – 8с9; 3) 125a3b3 + 64d3.
745. Розкладіть на множники многочлен, використовуючи формули скороченого множення:
1)16ab6c2 – 36; 2) 125a6b6 – 27m6; 3) 343 m3b9 + 8n6.
746. Який із наступних виразів дорівнює виразу х2 + 3х + х + 3:
1) (х+3)(х + 1);
2)(х+3)(3х + 1);
3) (х +1)(3х + 3)?
747. Чи правильно, що ху2 – х2у + х – у дорівнює:
1) (х – у)(ху – 1);
2) (х – у)(1 – ху);
3) (х + у)(ху – 1)?
У неправильних рівностях укажіть, де допущено помилку.
748. Розкладіть многочлен на множники способом групування:
1)2а3 + 4а + а2 + 2; 4) а3b + аb3+а2+ b2;
2) b3 – 3b2 + 5b – 15; 5) bс2 – b2с + 5b – 5с;
3) 16m4 – 8m3 + 6m – 3. 6)m2n2 – n4 + 6m2 – 6n2.
749. Розкладіть многочлен на множники способом групування:
1) 3х3 + х + 3х2 + 1;
2) 5а2 -15ab + 2а – 6b;
3) 0,4mn + 1,6 + 0,8m2n + 3,2m.
750. Уставте замість зірочки такий двочлен, щоб утворилася тотожність:
1) а3 – 2а2 + 4а – 8 = (а – 2) ∙ (*);
2) 2b4 – 6b3 + 9b – 27 = (*) ∙ (2b3 + 9).
751. Уставте замість зірочки такий двочлен, щоб утворилася тотожність:
1) х4 + 4х3 + 5х3 + 20 = (*) ∙ (х3 + 5);
2) 4b6 – 12b4 + 7b2 – 21 = (b2 – 3) ∙ (*).
752. Розкладіть на множники многочлен:
1) 21m2n + 14mn2+ 56m2n2;
2) 36m3n4 + 9m3n5 + 72m5n4;
3) 0,4х2у3 + 6,4х3у7 + 2,8х2у6+ 2,4х4y2.
753. Розкладіть на множники многочлен:
1) 32b5с6 + 24b13с10 + 16b8с8;
2) 16а12с4 + 64a7c7 + 48а9с3 + 80а8с6;
3) 15b5d6 + 225b4d7 + 45b8d5 + 60b10d12.
754. Розкладіть на множники вираз:
1) (2у + 3)2 – (5х + 1)2; 3) (3b + 5а)2 – (5b – 3а)2.
2) (4n2 +1 )2 – (3 + n2)2;
755. Розкладіть на множники вираз:
1) (2b + 3)2 – (5 + b)2; 3) (2m + 3)2 – (3 – 2m)2.
2) (5а + 4)2 – 25а2;
756. Подайте у вигляді добутку вираз:
1) (3ху + 4)2 – 9х2y2; 3) (7 + 6у2)2 – 36y4.
2) ( Ab + 5)2 –
Ab + 5)2 –  A2b2;
A2b2;
757. Подайте у вигляді добутку вираз:
1) (m2n2 + З)2 – m2n2; 3) (1,2а2 – 4)2 – 1,44а4.
2) ( X2y + 5)2 –
X2y + 5)2 – 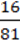 X4y2;
X4y2;
758. Розкладіть на множники вираз:
1) (3х + 4)3 – 27х3; 3) (4n2 + 1)3 + (1 – 4n2)3.
2) (-2b + 3а)3 + 8b3.
759. Подайте у вигляді добутку вираз:
1) а2 – х2 + 2х – 2а; 3)3х3 – 3у3 + 5х2 – 5у2.
2) х3 – 8 + (х + 2)2 – 2х;
760. Розкладіть на множники вираз і знайдіть його значення:
1) 16х4 – (2х – 1)4, якщо х = 0,5;
2) (2х + 5)3 – (2х – 5)3, якщо х = -0,1.
761. Подайте у вигляді добутку вираз:
1) а2(а + b) + 2а(а + b) + а + b;
2) х2(х + 2) – 4х(х + 2) + 4(х + 2);
3) 9m2(2m + 3) – 36(2m + 3).
762. Розкладіть на множники вираз:
1) 2 – а3b3 – ab;
2) (a + b)2 – с2 + a + b + с;
3) (a – b)2 – (c + d)2 – a + b – c – d.
763. Розкладіть на множники вираз:
1) (m – n)2 – р2 – 2m + 2n – 2р; 3)(а + b)3 + (а – b)3 – 2a3.
2) (а + b)3 – (а – b)3 – 2b;
764. Розкладіть на множники вираз:
1)(3х + 4)4 – 81х4;
2) (2а + 3b)4 – 9b2;
3) (5ху – 1)4 – 1.
765. Доведіть, що:
1) 43 – 1 ділиться на 7;
2) 1692 – 442 ділиться на 15;
3) 2222 – 782 ділиться на 360.
766. Подайте у вигляді добутку многочлен:
1) 9х2 + 6х +1 – 16y2; 3) 9с2 – 64 – 16d – d2.
2) 16 + 9b2 -12b -25а2;
767. Розкладіть на множники многочлен:
1)х2 – 5х + 6; 2)у2 – 3у + 2.
768. Розкладіть на множники многочлен:
1)Х2 – 8Х + 15; 2)m2 – 7m + 12.
769. Розкладіть на множники многочлен:
1) х4 + 5х2 – 6; 2) х4 – 3х2 – 4.
770. Розв’яжіть рівняння:
1) х2 – 16 = 0; 3)х2 – (3 + х)2 = 3х.
2) (2х -1)2 – 25 = 0;
771. Подайте у вигляді добутку многочлен:
1) х4 + х2 + 1; 2)х6 + х4 + х3 + х2 + х +1.
772. Розкладіть на множники вираз: х3 – (а + b + с)х2 + (ab + ac + bc)x – abc.
773. Розкладіть на множники вираз: у3(a – х) – х3(а – у) + а3(х – у).
774. Доведіть, що вираз n4 + 3n3 – n2 – 3m ділиться на 6 при будь – якому натуральному значенні n.
775. Доведіть, що вираз (2n – 1 )3 – (2n – 1) ділиться на 24 при будь-якому натуральному значенні n.
776. Розкладіть на множники многочлен:
1) а3 – 10а2 + 23а – 6; 2) 12х3 + 25х2 + 44х + 24.
777. За умови, що 2a2 + 4а – 1 = -6 за деякого значення змінної а, знайдіть значення виразу:
1) -6а2 – 12а +3;
2) а2 + 2а;
3) 12а4 + 48а3 + 42а2 – 12а.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
778. У трикімнатній квартирі одна кімната має підлогу форми квадрата зі стороною а, друга – форми квадрата зі стороною b, а третя – форми прямокутника зі сторонами a і b відповідно. Сума площ підлог першої, другої та подвоєної площі третьої кімнати дорівнює 49 м2. Знайдіть периметр кімнати, що має форму прямокутника.
779. Відомо, що різниця квадратів віку тата семикласниці Іринки та самої дівчинки дорівнює добутку чисел 49 і 25. Знайдіть вік тата і дівчинки.
ЗАДАЧІ НА ПОВТОРЕННЯ
780. Розв’яжіть рівняння:
1)|5х – 2) = 8; 2) 2|х| + 3(х – 1) = 5.
781. Перше число на 40 % більше за друге, а їх середнє арифметичне дорівнює 36. Знайдіть ці числа.
ПЕРЕВІРТЕ, ЯК ЗАСВОЇЛИ МАТЕРІАЛ
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Що таке многочлен?
2. Які члени многочлена називаються подібними?
3. Як звести многочлен до стандартного вигляду?
4. Який член многочлена називається старшим?
5. Що називається степенем многочлена? Як його визначити?
6. Що означає додати многочлени?
7. Які закони справджуються для дій першого ступеня з многочленами?
8. Як помножити одночлен на многочлен? Многочлен на многочлен?
9. Які закони справджуються для множення многочленів?
10. Сформулюйте теорему про квадрат суми двох одночленів.
11. Які тотожності називають формулами скороченого множення?
12. Запишіть формули для обчислення квадрата суми та квадрата різниці.
13. Який вираз називається повним квадратом? Неповним квадратом?
14. Чи можна згорнути повний квадрат у квадрат двочлена? А неповний квадрат?
15. Сформулюйте теорему про добуток суми і різниці двох одночленів.
16. Запишіть формулу різниці квадратів.
17. Чому дорівнює квадрат різниці двох одночленів?
18. Сформулюйте теорему про добуток суми двох одночленів і неповного квадрата їх різниці.
19. Запишіть формулу суми кубів.
20. Запишіть формулу різниці кубів.
21. Що означає розкласти многочлен на множники?
22. Які способи розкладання многочлена на множники ви знаєте?
23. Як перевірити, чи правильно виконали винесення спільного множника за дужки?
ТЕСТОВІ ЗАВДАННЯ
Уважно прочитайте задачі і знайдіть серед запропонованих відповідей правильну. Для виконання тестового завдання потрібно 10-15 хв.
№1
1. Знайдіть степінь многочлена 9m3 + 1 + 2m6 – m4 + 8m.
А. 9 Б. 3. В. 8. Г. 6.
2.Знайдіть добуток одночлена – а і многочлена а – 3b2
А. а2 – 3b2.
Б. – а2 + 3b2a.
В.-2а – 3b.
Г.-а2 + 3b2.
3. Зведіть подібні члени многочлена у + 1,1y – 6у3 + 2у – -1,1у3 – у2 – 0,1у + 7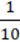 у3.
у3.
А. 2y – 2 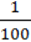 Y3 – y2.
Y3 – y2.
Б. 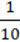 У3 – у2
У3 – у2
В. – y2.
Г. – у2 + 4y.
4. Знайдіть різницю многочленів 3х – х2 + 2 і – 13 + х2.
А. 3х – 9.
Б. 3х – 9 – 2х2.
В. 3х + 9 -2х2.
Г. 3х – 11.
5. Спростіть вираз: ( хy + 3а)(0,0625х2y2 –
хy + 3а)(0,0625х2y2 –  хуа + 9а2).
хуа + 9а2).
А. 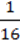 Х2y2 + 9а2
Х2y2 + 9а2
Б. 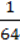 х3y3 + 27а3.
х3y3 + 27а3.
В. х3у3 + 27а3+ х2у2а.
х2у2а.
Г. 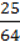 x3y3 + 27а3.
x3y3 + 27а3.
№2
1. Подайте вираз (7а + 5b)2 у вигляді многочлена.
А. 7а2 + 35аb + 5b2.
Б. 49а2 + 35аb + 25b2.
В. 49а2+ 70ab + 25b2.
Г. 7а2 + 70аb + 5b2.
2. Піднесіть до квадрата вираз 0,3х – 0,1 у.
A. 0,3х2 – 0,03ху + 0,1 у2.
Б. 0,9х2 – 0,06ху + 0,1 у2.
B. 0,09х2 – 0,06ху + 0,01 у2.
Г. 0,09х2 – 0,06xу – 0,01у2
3. Розкладіть многочлен 8с6 -125 на множники.
A. (2с2 – 5)(4с4 + 20с2 + 25).
Б. (2с3 – 5)(4с6 + 10с3 + 25).
B. (2с2 + 5)(4с4 -10с2 + 25).
Г. (2с2 + 5)(4с6 – 20с2 + 25).
4. Обчисліть, не користуючись калькулятором: 1012- 992.
А. 200. Б. 4. В. 400. Г. 1.
5. Розкладіть на множники вираз: (х – у)2 – z2 – 4х2 + 4хy + 4хz.
А. (х – у – z)(z – у – 3х).
В. (х – у + z)(z – у + 5х).
Б. (х – у + z)(2 – у – 4х).
Г. (х – у – z)(z + у + 3х).