Розкладання многочленів на множники способом групування
Розділ 1. ЦІЛІ ВИРАЗИ
& 13. Квадрат суми і квадрат різниці
Піднесемо до квадрата двочлен а + b:
(а + b)2 = (а + b)(а + b) = а2 + аb + bа + b2 = а2 + 2ab + b2. Отже,
Одержану тотожність називають формулою квадрата суми. Ця тотожність дає змогу підносити до квадрата суму двох довільних виразів не за правилом множення многочленів, а скорочено: одразу записувати квадрат (а + b)2 у вигляді а2 + 2аb + b2. Тому формулу квадрата суми називають ще формулою скороченого множення. Читають її так.
Приклад 1. Подайте вираз (3x + 5y)2 у вигляді многочлена.
Розв’язання.
(3х
Якщо проміжні дії можна виконати усно, то можливо одразу записувати відповідь:
(3х + 5у)2 – 9m2 + 30ху + 25y2.
Піднесемо тепер до квадрата двочлен а – b:
(а – b)2 = (а – b)(а – b) = а2 – аb – bа + b2 = а2 – 2аb і b2.
Отже,
Одержали формулу квадрата різниці, яка також є формулою скороченого множення. Читають її так.
Зауважимо, що формулу квадрата різниці можна одержати, якщо переписати різницю а – b у вигляді суми а + (- b):
(а – b)2 = (а + (-b))2 = а2 + 2а ∙ (-b) + (-b) = а2 – 2аb + b2.
Приклад 2. Піднести двочлен 4а – 7b до квадрата.
Р о з в’ я з а н н я. За формулою
Нам уже відомо, що x2 = (-x)2, тому при піднесенні до квадрата виразів вигляду – а – b і – а + b доцільно попередньо замінити їх на протилежні їм вирази:
Приклад 3. Перетворити на многочлен:
1) (-х – 6m)2;
2) (- 2р2 + 9q)2.
Розв’язання.
1) (-x – 6m)2 = (х + 6m)2 = x2 + 12xm + 36m2;
2) (-2р2 + 9q)2= (2р2 – 9q)2= 4р4 – 36p2q + 81q2.
Приклад 4. Спростити вираз (-5m3 – 2n2)2 + (2m3 – 5n2)2.
Р о з в ‘ я з а н н я. (-5m3 – 2n2)2 + (2m3 – 5n2)2 = (5m3 + 2n2)2 + 4m6 – 20m3n2 + 25n4 = 25M6 + 20M3N2 + 4N4 + 4m6 – 20M3N2 + 25N4 = – 29m6 +29n4.
A ще раніше…
Деякі правила скороченого множення були відомі стародавнім китайським і грецьким математикам більше ніж 4 тисячі років тому. Тоді вони формулювали ці правила не за допомогою букв, а словами, і доводили геометрично, тобто тільки для додатних чисел.
Наприклад, тотожність (а + b)2 = а2 + 2аb + b2 у другій книзі “Начал” Евкліда (III ст. до н. е.) формулювалася так: “Якщо пряма лінія (мається на увазі відрізок) як-небудь розсічена, то квадрат на всій прямій дорівнює квадратам на відрізках разом із двічі узятим прямокутником, що міститься між відрізками”. Тут “квадрат на всій прямій” слід розуміти як (а +b)2, “квадрати на відрізках” як а2 і b2, “прямокутник, що міститься між відрізками” як ab.
Геометричний зміст цієї тотожності зображено на малюнку 4.
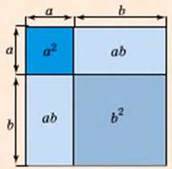
Мал. 4
Запишіть і прочитайте формулу квадрата суми. Запишіть і прочитайте формулу квадрата різниці. Як піднести до квадрата вирази – а – b і – а + b?
417. (Усно) Які з виразів є квадратами суми двох виразів, а які – квадратами різниці:
1) а2 + b2;
2) (m – n)2;
3) а2 – b2;
4) (с + 5);
5) (а + 2)2;
6) (а – 5)3;
7) (2 – р)2;
8) (t + m)2?
418. (Усно) Які з рівностей є правильними:
1) (а – 2)2 = а2 – 2а;
2) (b + 3)2 = b2 + 2 ∙ b ∙ 3 + 32;
3) (m + 5)2 = m2 + m ∙ 5 + 52;
4) (7 – р)2 = 72 – 2 ∙ 7 ∙ р + р2?
419. Які з рівностей є правильними:
1) (m – 3)2 = m2 – 2 ∙ m ∙ 3 + 32;
2) (р + 7)2=p2 + 72;
3) (2 – a) = 22 – 2 ∙ а + а2;
4) (b + 3)2 = b2 + 2 ∙ b ∙ 3 + 32?
420. Подайте у вигляді многочлена:
1) (a + c)2;
2) (m – х)2;
3) (b + t)2;
4) (р – у)2.
421. Піднесіть до квадрата:
1) (m – n)2;
2) (х + b)2;
3) (р – с)2;
4) (а + d)2.
422. (Усно) Подайте вираз у вигляді многочлена:
1) (а + 4)2;
2) (х – 3)2;
3) (b + 2)2;
4) (m – 5)2.
423. Піднесіть до квадрата:
1) (х – 5)2;
2) (а + 3)2;
3) (10 – m)2;
4) (7 + у)2;
5) (с – 0,2)2;
6) (0,8 + х)2.
424. Перетворіть на многочлен:
1) (2х + 5)2;
2) (7b – 4)2;
3) (10х + 3у)2;
4) (9а – 4)2;
5) ( х + 3у)2;
х + 3у)2;
6) (5m – 0,2t)2.
425. Перетворіть на многочлен:
1) (а – 3)2;
2) (х + 9)2;
3) (с + 0,3)2;
4) (2а – 5)2;
5) (4у + 3)2;
6) (9а – 8b)2;
7)(4b + 7а)2;
8) ( M – 2n)2 ;
M – 2n)2 ;
9) (0,5р + 2у)2.
426. Виконайте дії:
1) (3а + 1)2 – 1;
2) 12ab + (2а – 3b)2;
3) (4а + 8)2 – 16(а2 + 4);
4) – 4у2 – (5х – 2у)2 – 25х2.
427. Спростіть:
1) 20а + (а – 10)2;
2) (3m + 5)2 – 9m2;
3) (х + 4)2 – 8(х + 2);
4) (2а – 7b)2 – (4а2 + 49b2).
428. Перетворіть вираз на многочлен стандартного вигляду:
1) (а – 2)2 + а(а + 4);
2) (b + 1)(b + 2) + (b – 3)2.
429. Спростіть вираз:
1) (m – 5)2 – m(m – 10);
2) (х + 4)2 + (х + 1)(х – 9).
430. Розв’яжіть рівняння:
1) (х + 3)2 – х2 = 12;
2) (у – 2)2 = у2 – 2у.
431. Розв’яжіть рівняння:
1) (х – 4)2 – х2 = 24;
2) (у + 5)2 = 5у + у2.
432. Заповніть у зошиті таблицю за зразком:
Вираз I | Вираз II | Квадрат різниці виразів І і II |
2х | B | 4х2 – 4xb + b2 |
7b | 4х2 – 28хb + 49b2 | |
3х | 9×2 – 2хb + | |
0,5х | 4b |
433. Заповніть у зошиті таблицю за зразком:
Вираз І | Вираз II | Квадрат суми виразів І і II |
3m | А | 9m2 + 6mа + а2 |
5m | 25m2 + 20mа + 4а2 | |
4а |
| |
0,6m | 5a | |
|
434. За формулою квадрата суми або квадрата різниці обчисліть:
1) (100 + 2)2;
2) 412;
3) 992;
4) 3,82.
435. Обчисліть, використовуючи формули квадрата суми або квадрата різниці:
1) (40 – 1)2;
2) 892;
3) 5012;
4) 4,022.
436. Серед виразів (х – у)2, (х + у)2, (-у + х)2, (-х – у)2 знайдіть ті, що є тотожно рівними виразу:
1) (у + х)2;
2) (у – х)2.
437. Подайте у вигляді многочлена:
1) (-р + 5)2;
2) (-а – 7)2;
3) (-р – 2m2;
4) (-3b + с)2.
438. Перетворіть на многочлен:
1) (-а + 3)2;
2) (-b – 5)2;
3) (-4m + р)2;
4) (-а – 3b)2.
439. Перетворіть на многочлен:
1) (-9b + 4m)2;
2) (-7а – 10b)2;
3) (-0,5m – 0,4p)2;
4) (-1  Х + 6y)2;
Х + 6y)2;
5) (0,04p – 50q)2;
6) (-0,25с – 0,2d)2.
440. Подайте у вигляді многочлена:
1) (-3а + 5х)2;
2) (-8x – 5y)2;
3) (-4b – 0,5y)2;
4) (8x + 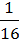 У)2;
У)2;
5) (-0,02а – 10b)2;
6) (-0,15m + 0,1n)2.
441. Виконайте дію:
1) (а2 – 9)2;
2) (7 – у3)2;
3) (2а + c4)2;
4) (-5а + b3)2;
5) (4а2 – 5m3)2;
6) ( P4 + 9q3)2.
P4 + 9q3)2.
442. Піднесіть до квадрата:
1) (а2 + 2a)2;
2) ( M3 -12m)2;
M3 -12m)2;
3)(1  P + 3p2)2;
P + 3p2)2;
4) (7ab – 2b3)2;
5) (10р6 + 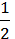 Р4a3)2;
Р4a3)2;
6) (0,2m2n + 15m3n4)2.
443.Подайте вираз у вигляді многочлена:
1) (b7 – 5)2;
2) (a3 + 2b4)2;
3) (8х6 –  х2)2;
х2)2;
4) 6m3 + 1  m5)2 ;
m5)2 ;
5) (7а2 + 8aр3)2;
6) (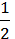 B2m3 –
B2m3 –  b3m2)2.
b3m2)2.
444. Спростіть вираз:
1) (3a – 4b) – (3a + 4b)2;
2) (2a – 3b)2 + (a – 6b)2;
3) a(2a – 1)2 – 4a(a + 5)2;
4) 12m2 – 3(2m – n)2 – 12mn.
445. Виконайте дії:
1) (7a + 9b)2 – (7a – 9b)2;
2) (10a – 3b)2 + (6a + 5b)2;
3) 18×2 – 12xy – 2(3x – y)2;
4) a(9a – 1)2 – 81a(a – 2)2.
446. Які одночлени треба записати замість зірочки, щоб утворилася тотожність:
1) (* + 2a)2 = b2 + 4ab + 4a2;
2) (2b – *)2 = 4b2 + 9 – 12b;
3) (3a4 + *)2 = * + 30a4 + 25;
4) (5×2 – *)2 = 25×4 – * + 9m2?
447. Замініть зірочку одночленом так, щоб одержати тотожність:
1) (* – 7)2 = х2 – 14x + 49;
2) (4р3 + *)2= * + 9 + 24р3.
448. Подайте вираз у вигляді многочлена стандартного вигляду:
1) (x – 2)(х + 1)2;
2) (х + 1)(x – 5)2.
449. Доведіть тотожність:
1) (а + b)2 + (а – b)2 = 2(а2 + b2);
2) m2 + n2 = (m + n)2 – 2mn.
450. Доведіть тотожність:
1) 4аb = (а – b)2 – (а + b)2;
2) (х – y)2 + 2xу = х2 + y2.
451. Розв’яжіть рівняння:
1) (3x – 4)2 – (3x + 2)2 = -24;
2) (2х – 3)2 + (1 – x) (9 + 4x) = 18.
452. Розв’яжіть рівняння:
1) х(х – 2) – (х + 5)2 = -1;
2) (2у – 7)2 + (5 – 4y)(y – 7) = 3(у – 6).
453. Використовуючи малюнок 5, поясніть геометричний зміст формули (а – b)2 = а2 – 2ab + b2 для а > 0, b > 0, а > b.
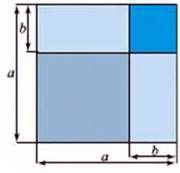
Мал.5
454. Спростіть вираз:
((((а + b)2 – 2аb)2 – 2а2b2)2 – 2a4b4)2 – 2а8b8.
455. Доведіть формулу скороченого множення для:
1) куба суми: (а + b)3 = а3 + 3а2b + 3аb2 + b3;
2) куба різниці: (а – b)3 = а3 – 3а2b + 3ab2 – b3.
Р о з в ‘ я з а н н я.
1) (а + b)3 = (а + b)2(а + b) = (а2 + 2аb + b2)(а + b) = а3 + а2b + 2а2b + 2аb2 + b2a + b3 = а3 + 3а2b + 3аb2 + b3.
456. Піднесіть до куба за формулами скороченого множення:
1) (а + 2)3;
2) (2b – 1)3.
457. Піднесіть до куба:
1) (х – 2)3;
2) (2m + 1)3.
Вправи для повторення
458. Знайдіть значення виразy:
(5,4: 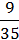 – 11
– 11  ) ∙ 2,25 – 4
) ∙ 2,25 – 4  .
.
459. Знайдіть три послідовних парних натуральних числа, якщо добуток двох менших з них на 104 менший від добутку двох більших.
460. Доведіть, що значення виразу:
1) 810 – 89 + 88 є кратним числу 152;
2) 154 – 104 – 54 ділиться на 80.
Цікаві задачі для учнів неледачих
461. Доведіть, що при будь-якому натуральному значенні n значення виразу (n2 + n)(n + 2) ділиться на 6.
 b2
b2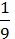 M2 + 6mа + 81а2
M2 + 6mа + 81а2