Розкладання многочленів на множники за допомогою формул квадрата суми і квадрата різниці
Розділ 1. ЦІЛІ ВИРАЗИ
& 14. Розкладання многочленів на множники За допомогою формул квадрата суми і квадрата різниці
Формули квадрата суми і квадрата різниці можна використовувати також для розкладання на множники виразів вигляду а2 + 2аb + b2 і а2 – 2ab +b2. Для цього перепишемо ці формули, помінявши місцями їх ліву і праву частини.
Такий вигляд формул зручно використовувати для перетворення тричлена у квадрат двочлена.
Тричлен вигляду а2 + 2ab + b2 або а2 – 2ab + b2 називають повним квадратом. Саме його можна подати у вигляді квадрата
Наприклад, х2 + 4х + 4 = (х + 2)2 і а2 – 6а + 9 = (а – 3)2, тому тричлени х2 + 4х + 4 і а2- 6а + 9 є повними квадратами. Перетворення тричлена, що є повним квадратом, у квадрат двочлена називають згортанням у повний квадрат.
Оскільки (а + b)2= (а + b)(а + b) і (а – b)2 = (а – b)(а – b), то згортання у повний квадрат є розкладанням тричлена па множники.
Приклад 1. Розкласти тричлен 4×2 + 12х + 9 на множники.
Р о з в ‘ я з а н н я. Оскільки 4х2 = (2х)2; 12х = 2 ∙ 2х ∙ 3 і 9 = З2, то тричлен 4х2 + 12х + 9 є квадратом суми 2х + 3, отже, його можна розкласти на множники:
4х2 + 12х + 9 = (2х)2 + 2 ∙ 2х ∙ 3 + 32 = (2х + 3)2.
Приклад 2. Знайти значення виразу х2 +
Р о з в’ я з а н н я. Спочатку згорнемо тричлен у повний квадрат:
Х2 + 25у4 – 10ху2 = х2 – 10ху2 + 25у4 = х2 – 2 ∙ х ∙ 5у2 + (5у2)2 = (х – 5у2)2.
Тепер виконати обчислення буде зовсім нескладно. Якщо х = 44, у = -3, то (х – 5у2)2 = (44 – 5 ∙ (-3)2)2∙ (44 – 45)2 = (-1) = 1.
Приклад 3. Перетворити тричлен -16а2 + 8ab – b2 на вираз, протилежний квадрату двочлена.
Р о з в ‘ я з а н н я. Винесемо за дужки -1, а одержаний в дужках вираз згорнемо в повний квадрат:
-16а2 + 8ab – b2 = -(16а2 – 8ab + b2) = -((4а)2 – 2 ∙ 4а ∙ b + b2) = -(4а – b)2.
Наведіть приклад тричлена, що є квадратом суми; квадратом різниці.
462. (Усно) Розкладіть на множники:
1) m2 + 2mn + n2;
2) р2 ∙ 2pq + q2;
3) а2 + 2 ∙ а ∙ 3 + З2.
463. Подайте тричлен у вигляді квадрата двочлена:
1) с2 – 2cd + d2;
2) x2 + 2xy + y2;
3) m2 – 2 ∙ m ∙ 5 + 52.
464. Розкладіть тричлен на множники:
1) t2 + 2tp + р2;
2) а2 – 2ах + х2;
3) b2 + 2 ∙ b ∙ 7 + 72.
465. Розкладіть на множники:
1) а2 – 6а + 9;
2) 64 + 16b + b2;
3) 0,01m2 + 0,2m + 1;
4)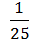 –
–  P + p2;
P + p2;
5) 4m2 – 12m + 9;
6) 9c2 + 24cd + 16d2.
466. Подайте вираз у вигляді квадрата двочлена:
1) а2 + 4а + 4;
2) 9m2 – 6m + 1;
3) b2 – 1,2b + 0,36;
4) 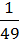 m2 –
m2 –  M + 1;
M + 1;
5) 81а2 + 18аb + b2;
6) 25m2 – 60mn + 36n2.
467. Знайдіть значення виразу, попередньо згорнувши його у повний квадрат:
1) а2 – 2а + 1, якщо а = 91; -19;
2) 4m2 + 28m + 49, якщо m = -3,5; 0;
3) 16х2 – 40ху + 25у2, якщо х = 5, у = 4.
468. Знайдіть значення виразу:
1) а2 + 10а + 25, якщо а = -15; 95;
2) 0,01×2 + 0,8x + 16, якщо х = 10; 40;
3) 4m2 + 28mn + 49n2, якщо m = 3, n = –  .
.
469. Обчисліть зручним способом:
1) 362 + 2 ∙ 36 ∙ 14 + 142;
2) 1172 – 2 ∙ 117 ∙ 17 + 172.
470. Обчисліть зручним способом:
1) 872 + 2 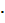 87 ∙ 13 + 132;
87 ∙ 13 + 132;
2) 1372 – 2 ∙ 137 ∙ 47 + 472.
471. Перетворіть тричлен у квадрат двочлена:
1)  m2 + 4n2 + 2mn;
m2 + 4n2 + 2mn;
2) – 10mn + 0,25m2+ 100n2;
3) 9р2 + pq + 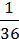 Q2;
Q2;
4) m6 + 4n2 – 4m3n;
5) 25m12 + p6 – 10m6p3;
6) 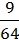 C6 – 3dc5 + 16d2c4.
C6 – 3dc5 + 16d2c4.
472. Розкладіть на множники:
1)  A4 + 9b2 + 2a2b;
A4 + 9b2 + 2a2b;
2) -6,4а2у4 + 0,16a4 + 64y8;
3) 16m20 + n12 – 8m10n6;
4) 6а4b2 + a6 + 9a2b4.
473. Подайте тричлен у вигляді квадрата двочлена або вираза, протилежного до квадрата двочлена:
1) -1 + 4х – 4х2;
2) -40а + 25а2 + 16;
3) 24ху – 9х2 – 16у2;
4) -140x3y + 100х6 + 49y2;
5) 4pq – 25р2 – 0,16q2;
6) -0,64m6 – 1,6m3n2 – n4.
474. Подайте тричлен у вигляді квадрата двочлена або виразу, що є протилежним до квадрата двочлена:
1) -9 – 30х – 25х2;
2) -36b + 81b2 + 4;
3) 42ху – 49×2 – 9у2;
4) -0,36а4 – 25b6 + 6а2b3.
475. Розв’яжіть рівняння:
1) х2 – 10х + 25 = 0;
2) 64у2 + 16у + 1 = 0;
3) 9×2 + 1 = -6х;
4) 16y2 – 56y = 49.
476. Розв’яжіть рівняння:
1) х2 + 16х + 64 = 0;
2) 36х2 – 12х +1 = 0;
3) 4х2 + 9 = -12х;
4) х2 = 0,4х – 0,04.
477. Запишіть замість зірочки такий одночлен, щоб одержаний тричлен можна було перетворити на квадрат двочлена:
1) * – 2mn + n2;
2) 25а2 + 20а + *;
3) 64m2 + * + 49b2;
4) * – 12bm3 + 9b2;
5) р2 – 0,8р7 + *;
6) * + а2b3 +  А4.
А4.
478. Запишіть замість зірочки такий одночлен, щоб одержаний тричлен можна було подати у вигляді квадрата двочлена:
1) * – 28х + 49;
2) 64а2 – 16а + *;
3) 25а2 + * + 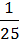 B6;
B6;
4) 0,01а8 + 100b6 + *.
479. Розкладіть вираз на множники:
1) (х – 2)2 + 2(х – 2) + 1;
2) (а2 + 6а + 9) + 2(а + 3) + 1.
480. Доведіть, що нерівність є правильною при будь-якому значенні х:
1) х2 + 2 > 0;
2) х2 – 6х + 9 ≥ 0.
481. Порівняйте з нулем значення виразу:
1) х2 – 4х + 4;
2) х2 + 2х – 1.
482. Вставте пропущені знаки ≤ або ≥ так, щоб при будь-яких значеннях х нерівність була правильною:
1) х2 + 4х + 4 … 0;
2) – х2 + 30х – 225 … 0;
3) – x2 – 8х – 16 … 0;
4) 36 – 12х + х2 … 0.
483. Доведіть, що при будь-яких значеннях змінної вираз х2 + 4х + 5 набуває лише додатних значень. Якого найменшого значення набуває цей вираз і при якому значенні х?
484. Доведіть, що при будь-якому значенні змінної вираз х2 + 6х + 11 набуває лише додатних значень. Якого найменшого значення набуває цей вираз і при якому значенні х?
485. Замініть зірочки одночленами так, щоб одержаний тричлен був повним квадратом (знайдіть три різних розв’язки задачі):
1) * – 48ху + *;
2) * + 20ab + *.
486. Подайте вираз у вигляді квадрата двочлена, якщо де можливо:
1) х2 – 3х + 9;
2) 49а2 – 140аb + 100b2;
3) 4а2 – 9b2 – 12аb;
4) 16у2 + 8y – 1;
5)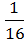 х2 +
х2 + 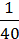 Ху +
Ху + 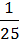 У2;
У2;
6) – xy + 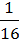 У2 + 4х2.
У2 + 4х2.
Вправи для повторення
487. При яких значеннях х:
1) квадрат двочлена х + 2 на 225 більший за квадрат двочлена х – 3;
2) квадрат двочлена 2х – 6 у 4 рази більший за квадрат двочлена х + 3?
488. Спростіть вираз:
1) (m – 2)(m + 3)(m – 5);
2) (р2 + 1)(р8 – p6 + p4 – р2 + 1).
Цікаві задачі для учнів неледачих
489. Маємо пісочні годинники двох видів: одними відміряють 7 хв, а іншими – 11 хв. Як за допомогою цих годинників відміряти рівно 15 хв?